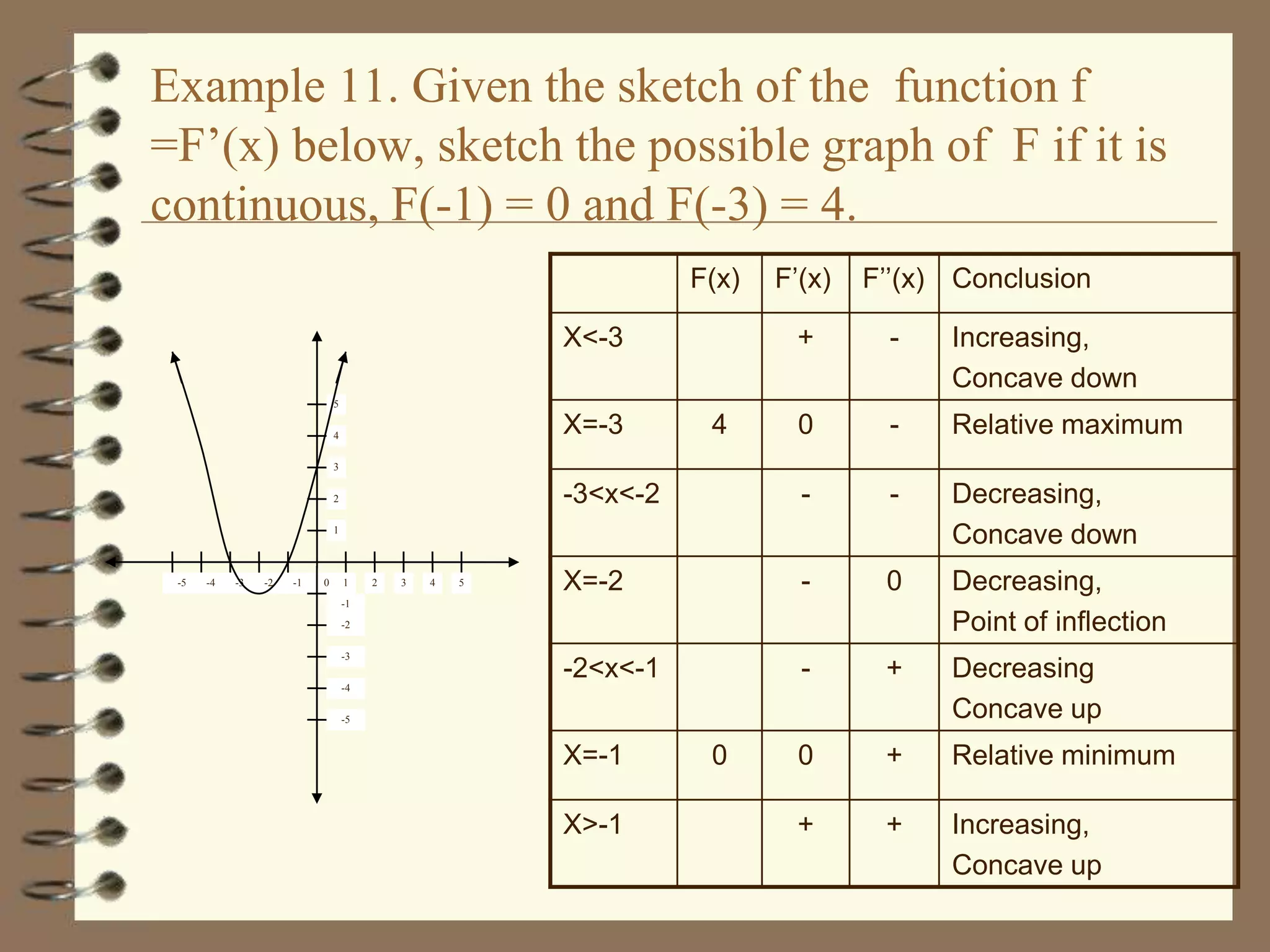
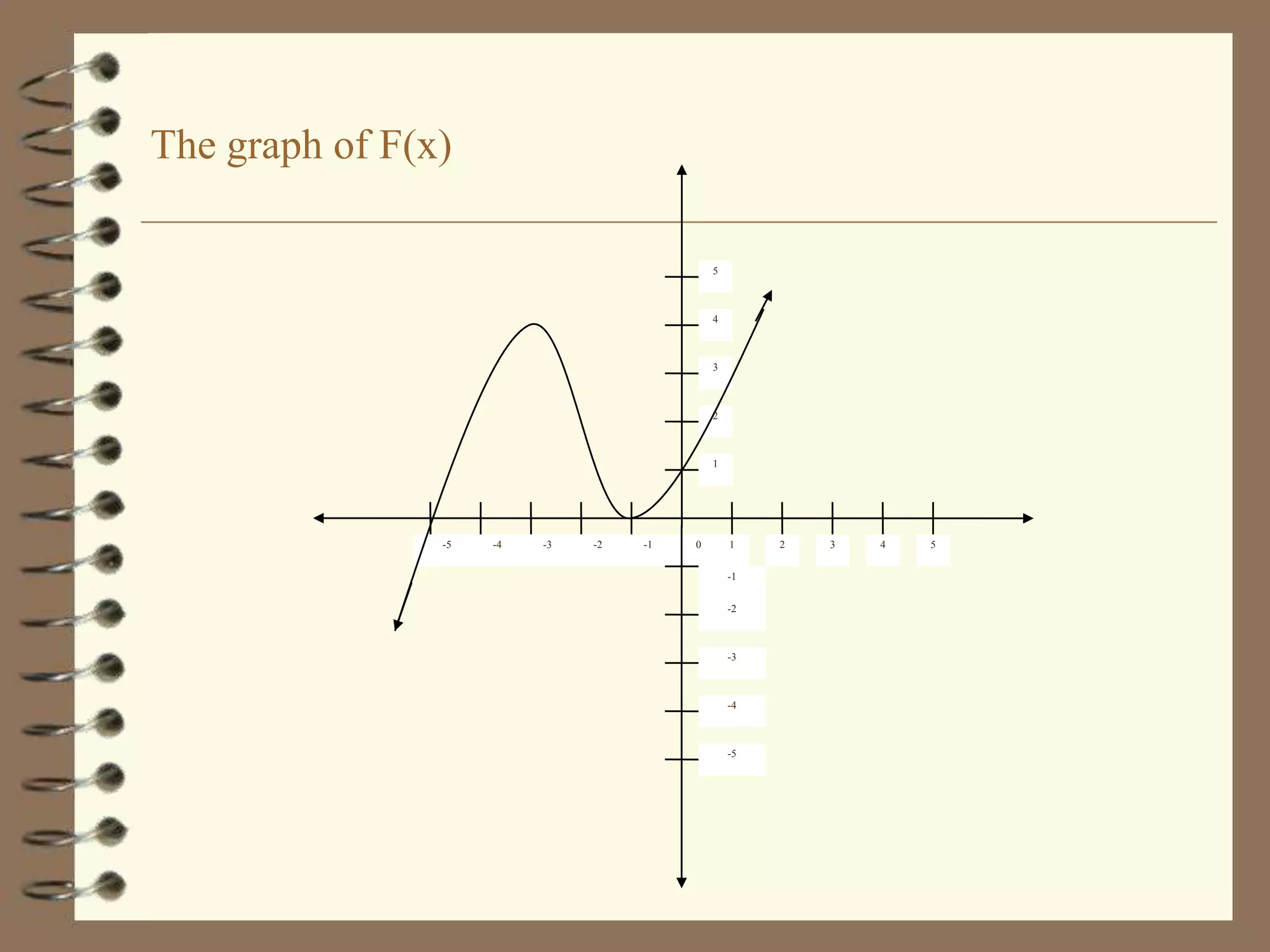
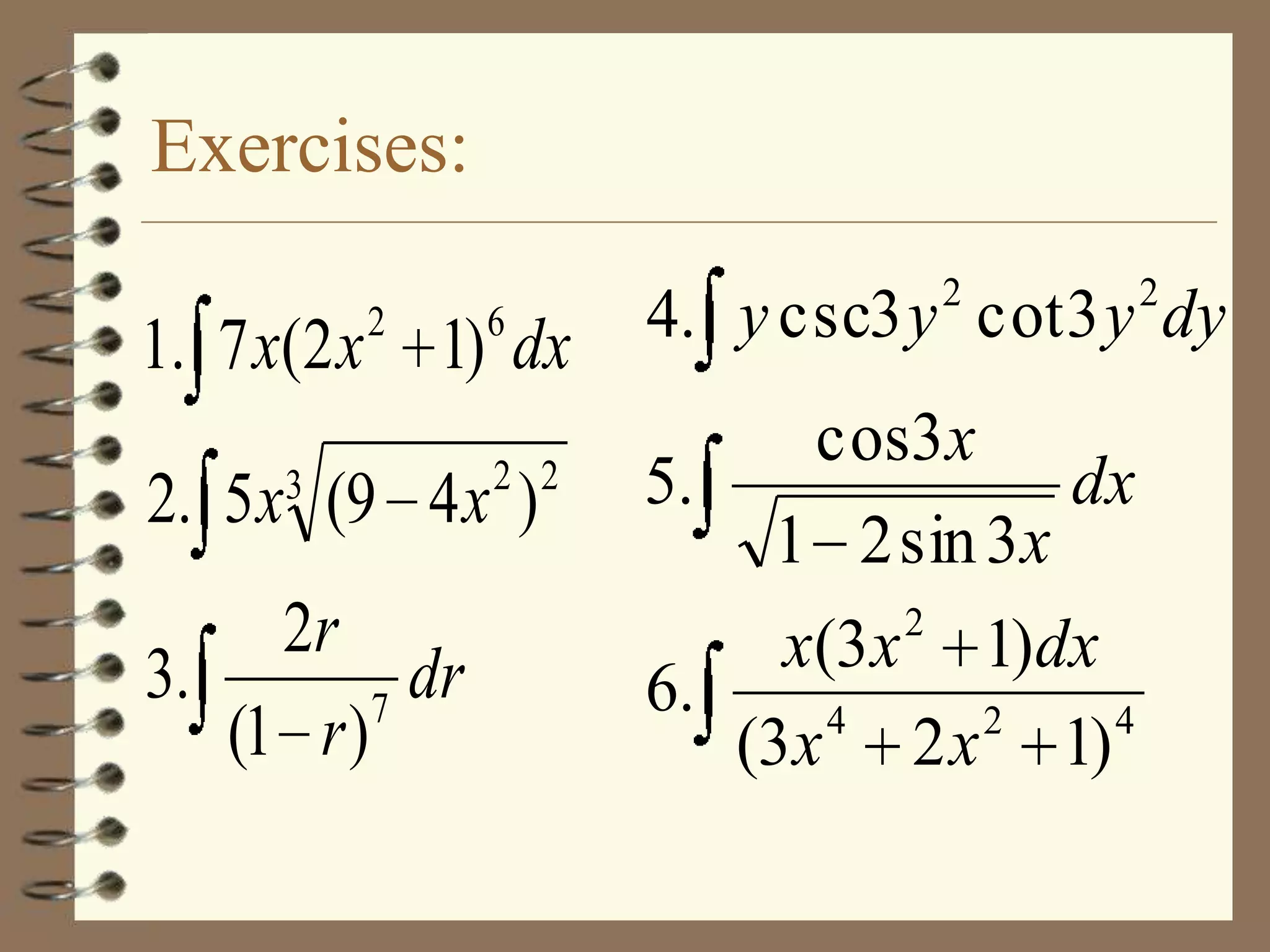Here are the steps to solve this problem: (a) Let t = time and y = height. Then the differential equation is: dy/dt = -32 ft/sec^2 Integrate both sides: ∫dy = ∫-32 dt y = -32t + C Initial conditions: at t = 0, y = 0 0 = -32(0) + C C = 0 Therefore, the equation is: y = -32t When y = 0 (the maximum height), t = 0.625 sec (b) Put t = 0.625 sec into the equation: y = -32(0.625) = -20 ft

1. Antiderivative/
Indefinite Integral

2. Find all possible functions
F(x) whose derivative is
f(x) = 2x+1
F(x) = x2 + x + 5
F(x) = x2 + x - 1000
F(x) = x2 + x + 1/8
F(x) = x2 + x - π
F(x) =
x2 + x

3. Definition
A function F is called an antiderivative (also an
indefinite integral) of a function f in the
interval I if
F '( x)
f ( x)
for every value x in the interval I.
The process of finding the antiderivative of a
given function is called antidifferentiation or
integration.

4. Find all antiderivatives
F(x) of f(x) = 2x+1
F(x) = x2 + x + 5
F(x) = x2 + x - 1000
F(x) = x2 + x + 1/8
F(x) = x2 + x - π
In fact, any function of the form F(x) =
x2 + x + c where c is a constant is an
antiderivative of 2x + 1
F(x) =
x2 + x

5. Theorem
If F is a particular antiderivative of f on an
interval I, then every antiderivative of f on I
is given by
F ( x) c
where c is an arbitrary constant, and all the
antiderivatives of f on I can be obtained by
assigning particular values for c. .

6. Notation
4 The symbol
denotes the operation of
antidifferentiation, and we write
f ( x)dx
F ( x) c
where F’(x)=f(x), and c is an arbitrary constant.
This is read “The indefinite integral of f(x)
with respect to x is F(x) + c".

7. f ( x)dx
F ( x) c
In this notation,
is the integral sign;
f(x) is the integrand;
dx
is the differential of x which denotes
the variable of integration; and
c
is called the constant of integration.
4 If the antiderivative of the function on interval
I exists, we say that the function is integrable
over the interval I.

8. Integration Rules
1. Constant Rule. If k is any real number, then
the indefinite integral of k with respect to x is
kdx
kx C
2. Coefficient Rule. Given any real number
coefficient a and integrable function f,
af ( x)dx
a f ( x)dx

9. Integration Rules
3. Sum and Difference Rule. For integrable
functions f and g,
[ f1 ( x)
f 2 ( x)]dx
f1 ( x)dx
f 2 ( x)dx
4. Power Rule. For any real number n,
where n ≠ -1, the indefinite integral xn of is,
n 1
n
x dx
x
C
n 1

10. Example 1.
(5 x 7)dx
5 xdx
7dx
5 xdx
7dx
1
2
5( x
5
2
x
2
2
C1 ) 7 x C2
7x C

11. Example 2.
6x
4
9x
2
x dx
4
6 x dx
9 x dx
4
1
2
2
x 2 dx
1
6 x dx 9 x dx
6
5
x
5
9
3
x
3
2
3
x
3
2
x 2 dx
C

12. Example 3.
3
5x 2
dx
5
x3
5x
4
4
2x
3
5
3
dx
5
5 x dx 2 x 3 dx
15
7
x
7
3
3
3
2
x
2
3
C

13. Integration Formulas for
Trigonometric Functions
sin x dx
cos x dx
2
sec x dx
cos x C
sin x C
tan x C
csc2 x dx
cot x C
sec x tan x dx
csc x cot x dx
sec x C
csc x C

14. Example 4.
2
(3 csc x cot x 7 sec x)dx
2
3 csc x cot xdx 7 sec xdx
3 csc x C1
7 tan x C2
3 csc x 7 tan x C

15. Example 5.
2
3 tan
4 cos
d
cos
1
3
tan d
4 cos d
cos
3 sec tan d
4 cos d
3 sec
C
4 sin

16. Exercises:
3
1. y ( 2 y
2.
3.
2
3)dy
x ( x 1)dx
y4
2 y2 1
dy
y
sin x
4.
dx
2
cos x
5. (2 cot2
3 tan 2 )d

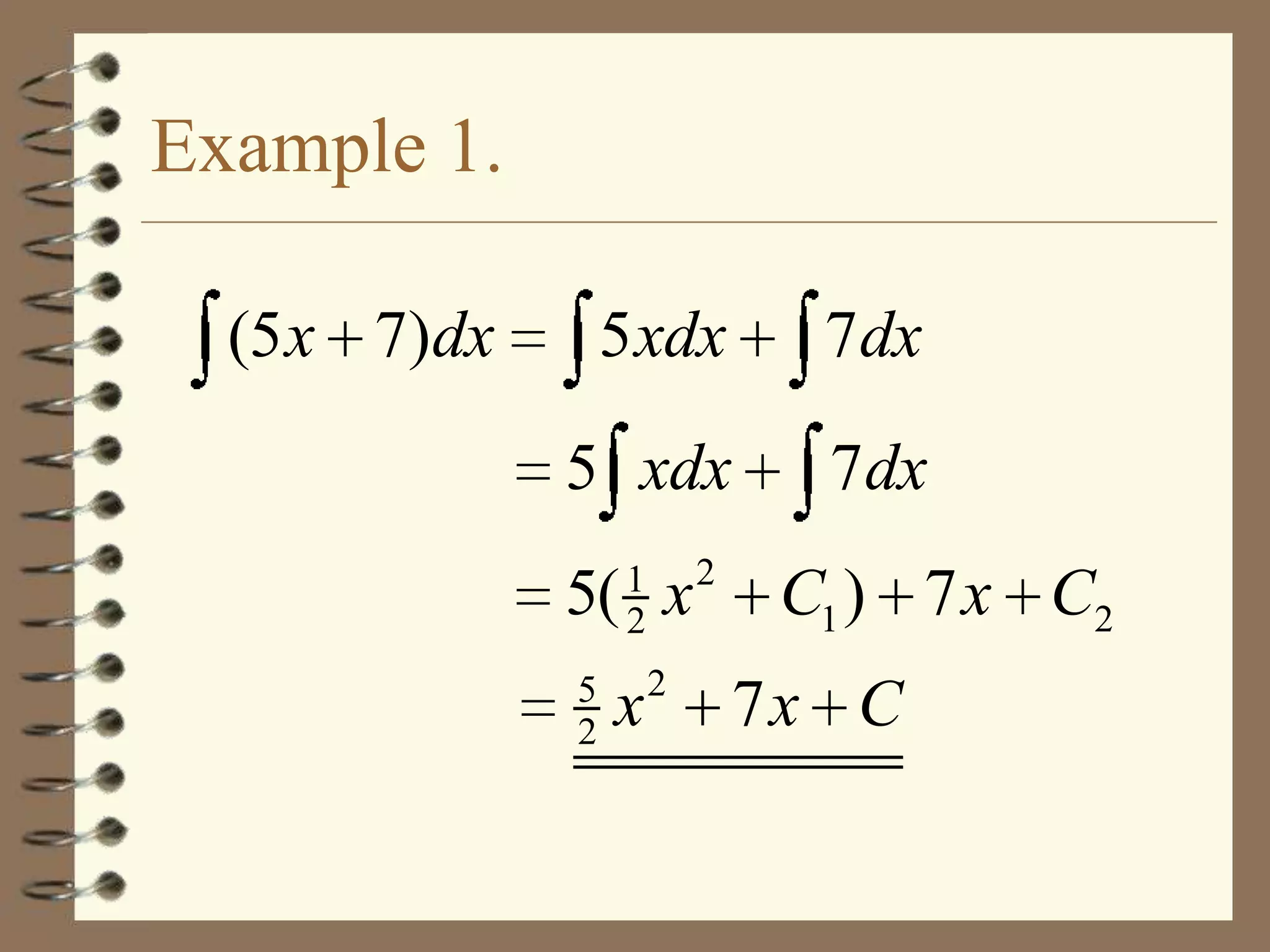
17. Integration by Chain Rule/Substitution
For integrable functions f and g
f ( g ( x))[ g '( x)dx] F ( g ( x)) C
where is an F antiderivative of f and C is an
arbitrary constant.

18. Example 6.
36 x
24
2
3
6x
4
6x
2 (6 x
2
8
5
(6 x
(6 x
5 dx
3
2
5 (18 x dx)
5) 4 (18 x 2 dx)
3
3
g’(x)=18x2
1
3
5)
5
Let g(x) = 6x3+5
5
4
C
4
5)
5
4
C

19. Example 6. Take 2!
36 x 2 4 6 x 3 5 dx 2
6 x 3 5 (18 x 2 dx)
4
4
2
u du
1
Let u = 6x3 + 5
2 (u ) du
2
8
5
8
5
u
5
u
5
4
du = 18x2 dx
4
C
4
5
C
4
(6 x
3
5)
5
4
C

20. Let g(t) = t4 + 2t
g’(t) = 4t3 + 2
Example 7.
2t 3 1
t4
2t
7
dx
= 2(2t3 + 1)
1 2(2t 3 1) dx
7
4
2
t 2t
1
2
1 t
2
t
4
4
12 t 4
7
2t
2t
6
C
6
1
2t
2(2t 3 1)dx
6
C

21. Example 8.
5
2
x (x
Let u = x2 -1
12
1) 2dx
du = 2x dx
x
2 2
(x
2
2
x2 = u+1
12
1) 2 xdx
12
(u 1) u du
(u
14
2u
13
1
15
u15
1
15
( x 2 1)15
2
14
12
u )du
u14
1
13
1
7
u13 C
( x 2 1)14
1
13
( x 2 1)13 C

22. Example 9.
sin 2 x 2 cos 2 x dx
1
2
2 cos 2 x (2 sin 2 xdx)
1
2
u (du )
1
2
Let u = 2 – cos2x
1/ 2
u (du )
1 2
2 3
1
3
du = 0 – (-sin2x)(2dx)
u 3/ 2
=2sin2xdx
C
(2 cos 2 x)
3/ 2
C

23. Example 10.
(tan 2 x cot 2 x) 2 dx
sin 2 x
cos 2 x
2
cos 2 x
sin 2 x
2
sin 2 x cos 2 x
cos 2 x sin 2 x
1
dx
2
2
cos 2 x sin 2 x
sec2 2 x csc2 2 xdx
2
dx
2
dx

24. Example 10.
sec2 2 x csc2 2 xdx
sec2 2 x(cot2 2 x 1)dx
2
2
sec 2 x cot 2 xdx
sec 2 xdx
(tan 2 x) 2 sec2 2 xdx
(tan 2 x) 2 2 sec2 2 xdx
1
2
1
2
(tan 2 x)
1
2
cot 2 x
1
1
2
1
2
2
sec2 2 xdx
1
2
tan 2 x C
tan 2 x C
2 sec2 2 xdx

25. Exercises:
1. 7 x(2 x
2
6
1) dx
3
2 2
2. 5 x (9 4 x )
2r
3.
dr
7
(1 r )
2
2
4. y csc3 y cot 3 y dy
cos3x
5.
dx
1 2 sin 3x
2
x(3x 1)dx
6.
4
2
4
(3x 2 x 1)

26. Applications of
Indefinite Integrals
1. Graphing
Given the sketch of the graph of the function,
together with some function values, we
can sketch the graph of its antiderivative
as long as the antiderivative is
continuous.

27. Example 11. Given the sketch of the function f
=F’(x) below, sketch the possible graph of F if it is
continuous, F(-1) = 0 and F(-3) = 4.
F(x)
X<-3
F’(x)
F’’(x) Conclusion
+
-
Increasing,
Concave down
0
-
Relative maximum
-3<x<-2
-
-
Decreasing,
Concave down
X=-2
-
0
Decreasing,
Point of inflection
-2<x<-1
-
+
Decreasing
Concave up
0
+
Relative minimum
+
+
Increasing,
Concave up
5
X=-3
4
4
3
2
1
-5
-4
-3
-2
-1
0
1
2
3
4
5
-1
-2
-3
-4
-5
X=-1
X>-1
0

28. The graph of F(x)
5
4
3
2
1
-5
-4
-3
-2
-1
0
1
-1
-2
-3
-4
-5
2
3
4
5

29. Applications of
Indefinite Integrals
1. Boundary/Initial Valued Problems
There are many applications of indefinite integrals
in different fields such as physics, business,
economics, biology, etc.
These applications usually desire to find particular
antiderivatives that satisfies certain conditions
called initial or boundary conditions, depending
on whether they occur on one or more than one
point.

30. Example 11.
Suppose we wish to find a particular
antiderivative satisfying the equation
dy
dx
6x 1
and the initial condition y=7 when x =2.

31. Sol’n of Example 11
dy
(6 x 1)dx
dy
(6 x 1)dx
2
y 3x
but x
x C
2 when
7 3(2)
2
3 C
y
C
7, then
7
Thus the particular antiderivative desired,
y
3x
2
x 7

32. Example 12.
The volume of water in a tank is V
cubic meters when the depth of water is h
meters. The rate of change of V with
respect to h is π(4h2 +12h + 9), find the
volume of water in the tank when the
depth is 3m.

33. Sol’n of Example 12
dV
dh
4h 2 12h
4h 2 12h
dV
V
4h3
3
0
4(03 )
6(02 )
3
C
6h 2
9 dh
9h
Volume V=0 if depth
h =0
C
9(0)
C
0
Thus V
V
9
4h3
3
4(33 )
6(32 )
3
6h 2
9(3)
9h
207
m3

34. The Differential Equations
Equation containing a function and its derivative or just its
derivative is called differential equations.
Applications occur in many diverse fields such as physics,
chemistry, biology, psychology, sociology, business,
economics etc.
The order of a differential equation is the order of the
derivative of highest order that appears in the equation.
The function f defined by y= f(x) is a solution of a
differential equation if y and its derivatives satisfy the
equation.

35. dy
6x 1
dx
dy (6 x 1)dx
dy
(6 x 1)dx
y 3x 2 x C
but x 2 when
7 3(2) 2 3 C
y
C
7, then
7
Thus find the particular solution
y
3x
2
x 7

36. If each side of the differential equations
involves only one variable or can be
reduced in this form, then, we say that these
are separable differential equations.
Complete solution (or general solution)
y = F(x) + C
Particular solution – an initial condition is
given

37. Example 13. Find the complete
solution of the differential equation
d2y
2
dx
d2y
dx 2
let
2
d y dy
4x 3
2
dx
dx
dy (4 x 3)dx
dy
y
(4 x 3)dx
2x
2
dy
dx
y
y
dy
dx
dy
dx
2 x 2 3 x C1
dy
3 x C1
d
dx
4x 3
(2 x
2
3
x3
3
2
2
3 x C1 )dx
x 2 C1 x C2

38. Example 14. Find the particular solution of
the differential equation in Ex. 13 for which
y=2 and y’=-3 when x=1.
y
2x
2
2
3 x C1
2
3
x3
2
3 x C1
3 2(1)
C1
y
2
3
(1)3
C2
8
y
2
3
x
3
3
2
x
2
8x
3
2
x 2 C1 x C2
3
2
(1) 2 8(1) C2
47
6
47
6

39. Example 16.
A stone is thrown vertically upward from the
ground with an initial velocity of 20ft/sec.
(a) How long will the ball be going up?
Ans. 0.625 sec
(b) How high will the ball go?
Ans. 6.25 ft
(c) With what velocity will the ball strike the
ground?
Ans. 20 ft/sec