Downloaded 21 times
Uploaded byAditya Abeysinghe Presentations
Waves 4
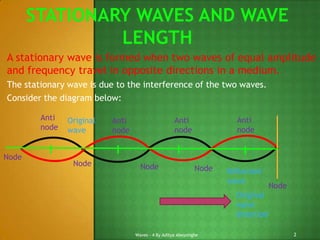
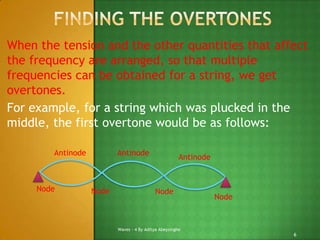
1) A stationary wave is formed by the interference of two waves traveling in opposite directions. Nodes occur where the waves destructively interfere, while antinodes occur where they constructively interfere. 2) The document discusses characteristics of stationary waves in strings and pipes, including how the fundamental frequency and overtones are determined based on the length, tension, and mass properties. 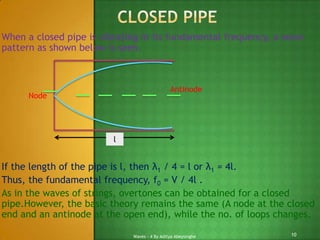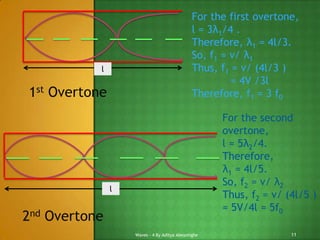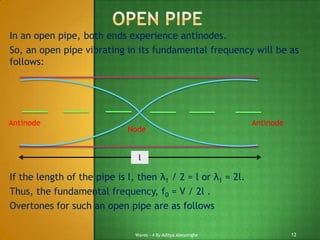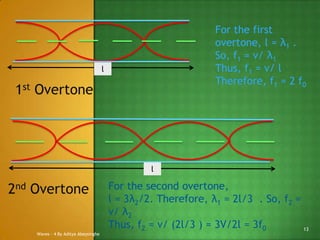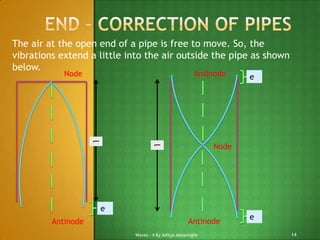3) For both closed and open pipes, the fundamental frequency and overtones follow specific patterns based on the length and wavelength. There is also an "end correction" to account for the air vibrations extending slightly outside the open end of the pipe.
More Related Content
More from Aditya Abeysinghe Presentations
Waves 4
- 1. Waves - 4By Aditya Abeysinghe See more at: Facebook – https://www.facebook.com/AdityaAbeysinghePresent ations Slideshare - slideshare.net/adityaabeysinghe Wordpress adityaabeysinghepresentations.wordpress.com/abeysi nghe-foundation/- afoundation/ 1
- 2. A stationary waveis formed when two waves of equal amplitude and frequency travel in opposite directions in a medium. The stationary wave is due to the interference of the two waves. Consider the diagram below: Anti node Node Original wave Node Anti node Anti node Anti node Node Node Reflected wave Node Original wave direction Waves - 4 By Aditya Abeysinghe 2
- 3. The following characteristicsare important to understand the wave. 1. At an antinode, the two waves have constructive interference. 2. At a node, the two waves have destructive interference. 3. Distance between consecutive nodes = λ /2 4. Distance between consecutive antinodes = λ /2 5. Distance from a node to the next antinode = λ /4, λ being the wave length. Waves - 4 By Aditya Abeysinghe 3
- 4. A transverse waveis formed when one end of a string is fixed and other end is moved up and down. See figure below. Speed of this vibration is given by, V = √T/ m , where T is the tension and m is the mass per unit length. Waves - 4 By Aditya Abeysinghe 4
- 5. Consider the diagrambelow. Antinode Node Node l If the wave length of the wire is λ , then l = λ /2. So, λ = 2l . Also, V = fλ . Thus, V = f . 2l or f = V/2l. However, we know that v = V = √T/ m . So, f = (1/2l) (√T/ m) This is the fundamental or lowest note obtained from the string . Thus, this frequency is commonly denoted by the symbol f0. Waves - 4 By Aditya Abeysinghe 5
- 6. When the tensionand the other quantities that affect the frequency are arranged, so that multiple frequencies can be obtained for a string, we get overtones. For example, for a string which was plucked in the middle, the first overtone would be as follows: Antinode Node Antinode Node Antinode Node Waves - 4 By Aditya Abeysinghe Node 6
- 7. Since the stringwas plucked in the middle, you’ll observe an antinode at that point. However, to remain symmetric, there will be three completely closed loops should be formed. Similarly, when the string is vibrating in the second overtone, to remain symmetric, five loops should be formed. Antinode Node Antinode Node Antinode Node Antinode Node Waves - 4 By Aditya Abeysinghe Antinode Node Node 7
- 8. Let’s calculate theindividual frequencies for the first and second overtones. (Length of the string = l) For the first overtone, l = 3λ1/2 . Therefore, λ1 = 2l/3 . So, f1 = v/ λ1 Thus, f1 = v/ (2l/3 ) or f1 = (3/2l) (√T/ m) For the second overtone, l = 5λ2/2. Therefore, λ1 = 2l/5 . So, f2 = v/ λ2 Thus, f2 = v/ (2l/5 ) or f2 = (5/2l) (√T/ m) Note that f1 = 3 f0 and f2 = 5 f0 . Thus, overtones are integer multiples of the fundamental frequency for a particular wave. Waves - 4 By Aditya Abeysinghe 8
- 9. Waves in pipesare similar to waves in strings. The only difference is that pipes are classified, unlike strings, as closed pipe and open pipe. The wave formation at the closed end of a closed pipe should be a node and at the opened end it should be an antinode. In contrast, in an open pipe, both ends are opened, so antinodes are formed at both ends. Waves - 4 By Aditya Abeysinghe 9
- 10. When a closedpipe is vibrating in its fundamental frequency, a wave pattern as shown below is seen. Antinode Node l If the length of the pipe is l, then λ1 / 4 = l or λ1 = 4l. Thus, the fundamental frequency, f0 = V / 4l . As in the waves of strings, overtones can be obtained for a closed pipe.However, the basic theory remains the same (A node at the closed end and an antinode at the open end), while the no. of loops changes. Waves - 4 By Aditya Abeysinghe 10
- 11. For the firstovertone, l = 3λ1/4 . Therefore, λ1 = 4l/3. So, f1 = v/ λ1 Thus, f1 = v/ (4l/3 ) = 4V /3l Therefore, f1 = 3 f0 l 1st Overtone For the second overtone, l = 5λ2/4. Therefore, λ1 = 4l/5. So, f2 = v/ λ2 Thus, f2 = v/ (4l/5 ) = 5V/4l = 5f0 l 2nd Overtone Waves - 4 By Aditya Abeysinghe 11
- 12. In an openpipe, both ends experience antinodes. So, an open pipe vibrating in its fundamental frequency will be as follows: Antinode Node Antinode l If the length of the pipe is l, then λ1 / 2 = l or λ1 = 2l. Thus, the fundamental frequency, f0 = V / 2l . Overtones for such an open pipe are as follows: Waves - 4 By Aditya Abeysinghe 12
- 13. For the first overtone,l = λ1 . So, f1 = v/ λ1 Thus, f1 = v/ l Therefore, f1 = 2 f0 l 1st Overtone l 2nd Overtone Waves - 4 By Aditya Abeysinghe For the second overtone, l = 3λ2/2. Therefore, λ1 = 2l/3 . So, f2 = v/ λ2 Thus, f2 = v/ (2l/3 ) = 3V/2l = 3f0 13
- 14. The air atthe open end of a pipe is free to move. So, the vibrations extend a little into the air outside the pipe as shown below. Antinode Node l l Node e Antinode e Antinode Waves - 4 By Aditya Abeysinghe e 14
- 15. As illustrated inthe diagram it should be noted that if the end correction is not negligible, (1) For a closed pipe the new wavelength would be λ/4 = l + e, so, λ = 4 (l + e). (2) For an open pipe the new wavelength would be λ/2 = l + e + e , since two end-corrections are required . So, λ = 2 (l + 2e). Experimental data show that e is approximately 0.3d , d being the diameter of a pipe, regardless whether it is closed end or open end. So, greater the diameter, greater will be the end correction. Waves - 4 By Aditya Abeysinghe 15