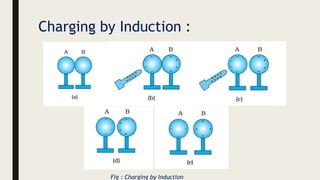
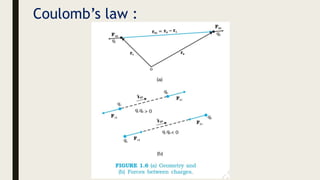
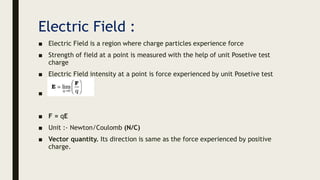
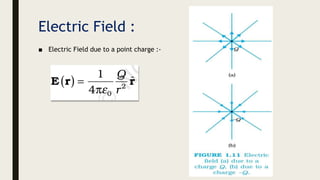
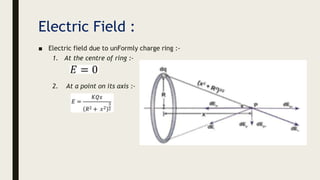
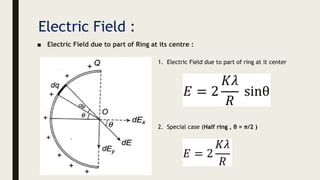
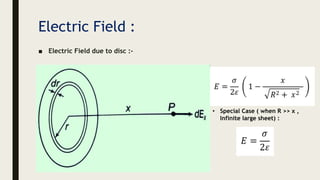
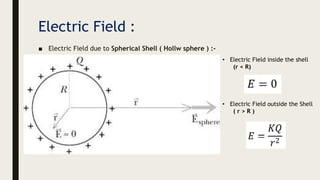
This document provides an overview of the key topics in electrostatics that will be covered in a chapter, including: electric charge, conductors and insulators, charging by induction, Coulomb's law, forces between multiple charges, electric fields, electric field lines, and electric field configurations such as those due to point charges, dipoles, conductors, and various charge distributions like shells and spheres. Formulas for calculating electric fields are presented.

1. ELECTROSTATIC
By :- Ashutosh Kumar
(B.Tech 2nd year )

2. Chapter overview :
■ Introduction
■ Electric Charge
■ Conductors and Insulators
■ Charging by Induction
■ Basic Properties of Electric Charge
■ Coulomb’s Law *
■ Forces between Multiple Charges *
■ Electric Field *
■ Electric Field Line

3. Chapter Overview :
■ Electrostatic Potential
■ Potential due to a Point Charge
■ Potential due to a System of Charges
■ Equipotential Surfaces
■ Potential Energy of a System of Charges
■ Potential Energy in an External Field

4. ChapterOverview :
■ Electric Field Lines
■ Electric Flux
■ Gauss’s Law
■ Applications of Gauss’s Law
■ Electric Dipole
■ Potential due to an Electric Dipole
■ Dipole in a Uniform External Field
■ Electrostatics of Conductors

5. Introduction :
■ All of us have the experience of seeing a spark or hearing a crackle whenwe
take off our synthetic clothes or sweater, particularly in dry weathe
■ The reason for these experiences isdischarge of electric charges through our
body, which were accumulateddue to rubbing of insulating surfaces.
■ You might have also heard thatthis is due to generation of static electricity
■ Static means anythingthat does not move or change with time
■ Ectrostatics deals with thestudy of forces, fields and potentials arising from
static charges.

6. Electric Charge :
■ Charge is of two type Posetive charge and Negative charge
■ (i) like charges repel
■ (ii) unlike charges attract each other.
■ Charge is always associated with mass. Massless particle cant have charge.
■ For Isolated system net Charge always remain conserve
■ Charge is invariant. Charge on any object doesn’t depens on refrence frame
■ SI unit of charge is Coulomb It is denoted by symbol C
■ In terms of this definition, one coulomb is the charge flowing through a wire in 1 s if
the current is 1 A (ampere)

7. Conductors and Insulators :
■ Some substances readily allow passage of electricity through them, others do
not
■ Those which allow electricity to pass through them easily are called
Conductors
■ They have electric charges (electrons) that are comparatively free to move
inside the material.
■ Metals, human and animal bodies and earth are conductors.
■ Most of the non-metals like glass, porcelain, plastic, nylon, wood offer high
resistance to the passage of electricity through them. They are called
insulators.

8. Charging by Induction :
Fig : Charging by Induction

9. Basic property of Electric charges :
■ Additivity of charges
■ Charge is conserved
■ Quantisation of charge
q = n e where n is any integer, positive or negative
■ This basic unit of charge is the charge that an electron or proton carries.
■ By convention, the charge on an electron is taken to be negative; therefore
charge on an electron is written as –e and that on a proton as +e.
■ The fact that electric charge is always an integral multiple of e is termed as
quantisation of charge
■ e = 1.602192 × 10 -19 C
■ Thus, there are about 6 × 1018 electrons in a charge of –1C

10. Coulomb’s law :
■ Coulomb measured the force between two point charges and found that
■ It varied inversely as the square of the distance between the charges (F ∝ 1/r2 )
■ It was directly proportional to the product of the magnitude of the two charges (F ∝
q1 q2 )
■ It acted along the line joining the two charges
■ K = 1/4πε0 = 9 × 109 Nm2/C2
■ ε0 is called the permittivity of free space
■ ε0 = 8.854 × 10–12 C2 N–1m–2

11. Coulomb’s law :

12. Forces between Multiple Charges :
■ Superposition Principle:
The principle is based on the property that the forces with which two
charges attract or repel each other are not affected by the presence of a
third (or more) additional charge(s).
For an assembly of charges q1, q2, q3, ..., the force on any charge, say q1,
is the vector sum of the force on q1 due to q2, the force on q1 due to
q3,and so on. For each pair, the force is given by the Coulomb’s law fortwo
charges stated earlier.

13. Forces between Multiple Charges :
• The force on q1 due to q2 is denoted by F12 is given by
• The force on q1 due to q3, denotedby F13, is given by

14. Forces between Multiple Charges :
■ Thus the total force F1 on q1 due to the two charges q2 and q3 is given
as
■ In General :

15. Electric Field :
■ Electric Field is a region where charge particles experience force
■ Strength of field at a point is measured with the help of unit Posetive test
charge
■ Electric Field intensity at a point is force experienced by unit Posetive test
charge
■
■ F = qE
■ Unit :- Newton/Coulomb (N/C)
■ Vector quantity. Its direction is same as the force experienced by positive
charge.

16. Electric Field :
■ Uniform Electric Field :-
If there exist uniform electric field in a region then force experienced by
any charge will be same at all the point

17. Electric Field :
■ Electric Field due to a point charge :-

18. Electric Field :
■ Electric Field due to system of point charges :-
• Electric field E1 at r due to q1 at r1 is given by
• Similarly Electric field E2 at r due to q2 at r2 is given by
• By the superposition principle, the electric field E at r
due to the system of charges is

19. Electric Field :
■ Electric field due to unFormly charge ring :-
1. At the centre of ring :-
2. At a point on its axis :-

20. Electric Field :
■ Electric Field due to part of Ring at its centre :
1. Electric Field due to part of ring at it center
2. Special case (Half ring , θ = π/2 )

21. Electric Field :
■ Electric Field due to uniform line charge :-
• Special Case ( when θ1 = θ2 , O is at mid of line )
• Special Case ( Infinite long line charge , θ = π ) =>

22. Electric Field :
■ Relation in line charge and charged part of ring :
θ
θ

23. Electric Field :
■ Electric Field due to disc :-
• Special Case ( when R >> x ,
Infinite large sheet) :

24. Electric Field :
■ Electric Field due to Spherical Shell ( Hollw sphere ) :-
• Electric Field inside the shell
(r < R)
• Electric Field outside the Shell
( r > R )

25. Electric Field :
■ Electric Field due to Solid Sphere
• Electric Field outside the solid sphere ( r >
R )
Volume charge density = ρ
or
• Electric field inside the solid sphere ( r < R )
or