By Ayushmaan Shrivastava and Aman Sharma

1. AMITY UNIVERSITY
RAJASTHAN
AMITY SCHOOL OF ENGINEERING AND
TECHNOLOGY
Presentati
on
on
Presented by:
Ayushmaan Shrivastava
Aman Sharma
B.Tech(CSE) - I Sem
Batch 2015-19
Presented to:
Dr. Umesh Dwivedi

2. AMITY UNIVERSITY
RAJASTHAN
AMITY SCHOOL OF ENGINEERING AND
TECHNOLOGY
Presentati
on
on
Presented by:
Ayushmaan Shrivastava
B.Tech(CSE) - I Sem
Batch 2015-19
Presented to:
Dr. K. C. Barmola

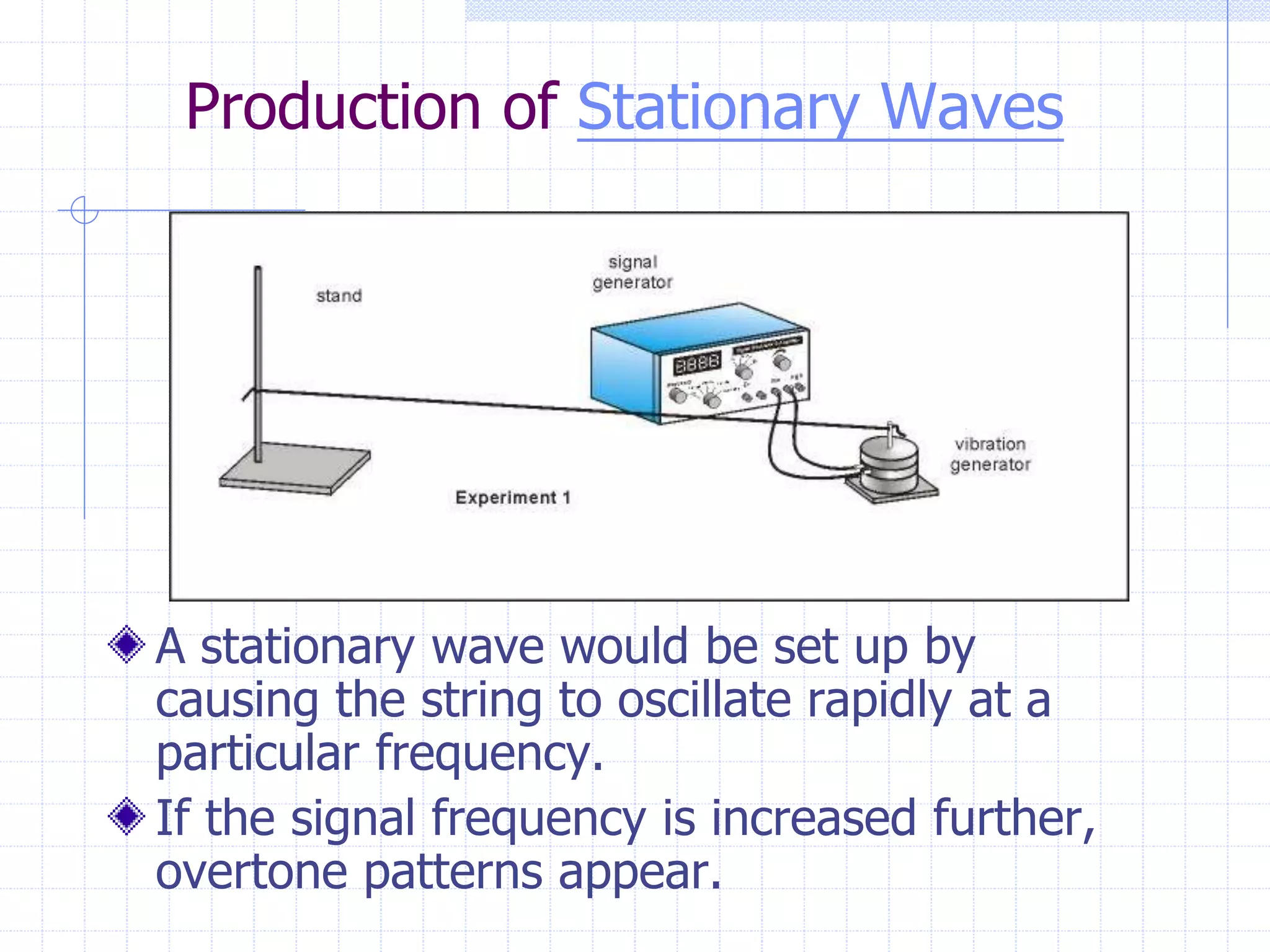
3. Stationary Waves
Stationary waves are produced by superposition
of two progressive waves of equal amplitude and
frequency, travelling with the same speed in
opposite directions.

4. Production of Stationary Waves
A stationary wave would be set up by
causing the string to oscillate rapidly at a
particular frequency.
If the signal frequency is increased further,
overtone patterns appear.

5. Properties of a stationary wave
Stationary waves have nodes where there is no
displacement at any time.
In between the nodes are positions called antinodes,
where the displacement has maximum amplitude.
l
A vibrating loop
N A N A N
Vibrator

6. Properties of a stationary wave
The waveform in a stationary wave does not move
through medium; energy is not carried away from the
source.
The amplitude of a stationary wave varies from zero
at a node to maximum at an antinode, and depends
on position along the wave.

7. Standing waves in a string fixed at both ends.
Normal modes of a string
...3,2,1,n
2

n
L
nl
...3,2,1,n
2

L
v
n
v
f
n
n
l
Wavelength:
Frequency:
1
...3,2,1,n
T
2
fnf
L
n
f
n
n




Tv :Using
frequencylfundamentathecalledis
T
2
1
1
L
f 

8. Standing waves in a string fixed at both ends.
f1 is called the fundamental frequency
The higher frequencies fn are integer
multiples of the fundamental frequency
These normal modes are called
harmonics.
f1 is the first harmonic, f2 is the second
harmonic and so on…

9. Investigating stationary waves using
sound waves and microwaves
Moving the detector along the line between the wave
source and the reflector enables alternating points of
high and low signal intensity to be found. These are the
antinodes and nodes of the stationary waves.
The distance between successive nodes or antinodes can
be measured, and corresponds to half the wavelength λ.
If the frequency f of the source is known, the speed of
the two progressive waves which produce the stationary
wave can be obtained.
Reflector
Detector
Wave source

10. Factors that determine the fundamental
frequency of a vibrating string
The frequency of vibration depends on
 the mass per unit length of the string,
 the tension in the string and,
 the length of the string.
The fundamental frequency is given by

T
L
fo
2
1
 where T = tension
 = mass per unit length
L = length of string

11. Standing Waves in a String
This is the first normal mode
that is consistent with the
boundary conditions.
There are nodes at both ends.
There is one antinode in the
middle.
This is the longest wavelength
mode:
 ½l1 = L so l1 = 2L
The section of the standing
wave between nodes is called a
loop.
In the first normal mode, the
string vibrates in one loop.
Section 18.3

12. Standing Waves in a String
Section 18.3

14. Progressive waves are the waves
originating from a source and travelling
forward in a medium is called a progressive
wave.
TRANSVERSE
WAVE
LONGITUDINAL
WAVES
Two types of progressive waves

15. TRANSVERSE WAVES:
• The waves propagates in the direction
perpendicular to the direction of vibration of
particles.
• The waves propagates in the form of crests and
troughs.

16. • Example of transverse waves:
vibration of a string, light, water.
ILLUSTRATION

17. LONGITUDINAL WAVES:
• The waves propagates in the direction parallel to the direction of
vibration of particles.
• The waves propagates as compressions and rarefactions.
• Example of longitudinal waves: sound waves and earthquake
waves.

18.  Longitudinal Waves are sometimes called
compression waves.
 They occur any time a medium is
compressed.
 As you can see from this diagram :

19.  In a longitudinal wave, the particles move
back and forth parallel to the wave's
direction.

22.  These waves advance in a medium
with finite velocity.
 All particle of the medium vibrate with
same amplitude.
 Phase of the vibrations vary
continuously from one particle to
another.

23.  No particle on the wave is permanently at rest
but comes to rest momentarily at its peak or
maximum displacement .

24.  Different particles reach the position of
maximum displacement at different time.
 All particles of the medium pass their mean
position in successions but with the same
velocity

25.  Pressure variations is same at all points of the
medium and travels forward.
 These waves transmit energy in medium in
direction of propagation.