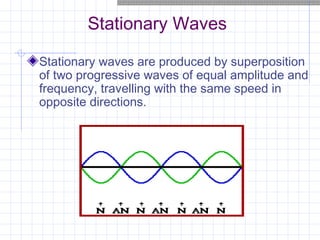
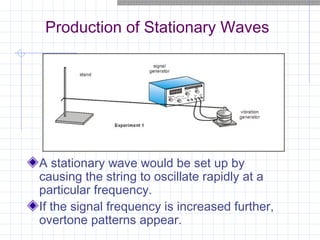
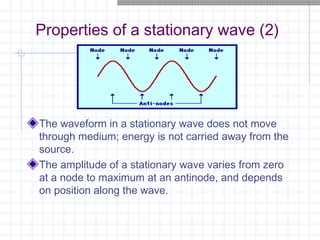
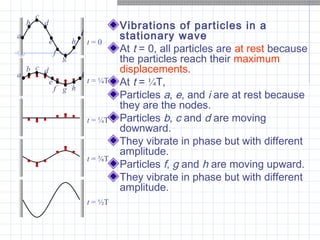
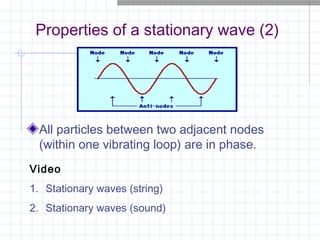
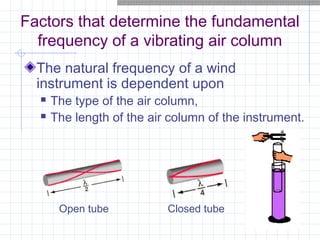
Stationary waves are produced by the superposition of two progressive waves of equal amplitude and frequency traveling in opposite directions. They have nodes where there is no displacement and antinodes where displacement is at maximum. A stationary wave's waveform does not move through the medium. Particles within a stationary wave vibrate in phase but with varying amplitudes, reaching maximum at antinodes and resting at nodes. The fundamental frequency and overtones of vibrating strings and air columns can be determined from measurements of stationary waves produced in them. The timbre of a sound depends on its harmonic content and amplitudes.

1. Stationary Waves
By
SATHISHKUMAR G
(sathishsak111@gmail.com)

2. Stationary Waves
Stationary waves are produced by superposition
of two progressive waves of equal amplitude and
frequency, travelling with the same speed in
opposite directions.

3. Production of Stationary Waves
A stationary wave would be set up by
causing the string to oscillate rapidly at a
particular frequency.
If the signal frequency is increased further,
overtone patterns appear.

4. Properties of a stationary wave (1)
Stationary waves have nodes where there is no
displacement at any time.
In between the nodes are positions called antinodes,
where the displacement has maximum amplitude.
λ
A vibrating loop
N A N A N
VibratorVibrator

5. Properties of a stationary wave (2)
The waveform in a stationary wave does not move
through medium; energy is not carried away from the
source.
The amplitude of a stationary wave varies from zero
at a node to maximum at an antinode, and depends
on position along the wave.

6. Vibrations of particles in a
stationary wave
At t = 0, all particles are at rest because
the particles reach their maximum
displacements.
At t = ¼T,
Particles a, e, and i are at rest because
they are the nodes.
Particles b, c and d are moving
downward.
They vibrate in phase but with different
amplitude.
Particles f, g and h are moving upward.
They vibrate in phase but with different
amplitude.
t = 0
t = ¼T
t = ¼T
t = ⅜T
t = ½T
a
b
c
d
e
f
g
h
ii
a
b c d
e
f g h
ii

7. Properties of a stationary wave (2)
All particles between two adjacent nodes
(within one vibrating loop) are in phase.
Video
1. Stationary waves (string)
2. Stationary waves (sound)

8. Modes of vibration of strings
Picture of Standing Wave Name Structure
1st Harmonic
or
Fundamental
1 Antinode
2 Nodes
2nd Harmonic
or
1st Overtone
2 Antinodes
3 Nodes
3rd Harmonic
or
2nd Overtone
3 Antinodes
4 Nodes
4th Harmonic
or
3rd Overtone
4 Antinodes
5 Nodes
5th Harmonic
or
4th Overtone
5 Antinodes
6 Nodes
L = ½λ1
f1 = v/2L
L = λ2
f2 = v/L
L = 1½λ3
f3 = 3v/2L
L = 2λ4
f4 = 2v/L
L = 2½λ5
f5 = 5v/2L
http://id.mind.net/~zona/mstm/physics/waves/standingWaves/standingWaves1/StandingWaves1.html
L

9. Investigating stationary waves using
sound waves and microwaves
Moving the detector along the line between the wave
source and the reflector enables alternating points of
high and low signal intensity to be found. These are the
antinodes and nodes of the stationary waves.
The distance between successive nodes or antinodes
can be measured, and corresponds to half the
wavelength λ.
If the frequency f of the source is known, the speed of
the two progressive waves which produce the stationary
wave can be obtained. Reflector
Detector
Wave source

10. Resonant Frequencies of a Vibrating
String
From the experiment, we find that
 There is a number of resonant frequencies
in a vibrating string,
 The lowest resonant frequency is called
the fundamental frequency (1st
harmonic),
 The other frequencies are called overtones
(2nd
harmonic, 3rd
harmonic etc.),
 Each of the overtones has a frequency
which is a whole-number multiple of the
frequency of the fundamental.

11. Factors that determine the fundamental
frequency of a vibrating string
The frequency of vibration depends on
 the mass per unit length of the string,
 the tension in the string and,
 the length of the string.
The fundamental frequency is given by
µ
T
L
fo
2
1
= where T = tension
µ = mass per unit length
L = length of string

12. Vibrations in Air Column
When a loudspeaker producing sound is
placed near the end of a hollow tube, the tube
resonates with sound at certain frequencies.
Stationary waves are set up inside the tube
because of the superposition of the incident
wave and the reflected wave travelling in
opposite directions.
http://www.walter-fendt.de/ph11e/stlwaves.htm

13. Factors that determine the fundamental
frequency of a vibrating air column
The natural frequency of a wind
instrument is dependent upon
 The type of the air column,
 The length of the air column of the instrument.
Open tube Closed tube

14. Name
Modes of vibration for an open tube
Picture of Standing Wave Structure
1st Harmonic
or
Fundamental
2 Antinodes
1 Node
2nd Harmonic
or
1st Overtone
3 Antinodes
2 Nodes
3rd Harmonic
or
2nd Overtone
4 Antinodes
3 Nodes
4th Harmonic
or
3rd Overtone
5 Antinodes
4 Nodes
5th Harmonic
or
4th Overtone
6 Antinodes
5 Nodes
L = ½λ1
f1 = v/2L
L = λ2
f2 = v/L
L = 1½λ3
f3 = 3v/2L
L = 2λ4
f4 =2v/L
L = 2½λ5
f5 = 5v/2L

15. Modes of vibration for a closed tube
Picture of Standing Wave Name Structure
1st Harmonic
or
Fundamental
1 Antinode
1 Node
3rd Harmonic
or
1st Overtone
2 Antinodes
2 Nodes
5th Harmonic
or
2nd Overtone
3 Antinodes
3 Nodes
7th Harmonic
or
3rd Overtone
4 Antinodes
4 Nodes
9th Harmonic
or
4th Overtone
5 Antinodes
5 Nodes
L = ¼λ1
f1 = v/4L
L = ¾λ3
f3 =3v/4L
L = 1¼λ5
f5 =5v/4L
L = 1¾λ7
f7 = 7v/4L
L = 2¼λ9
f9 =9v/4L

16. The quality of sound (Timbre)
The quality of sound is determined by the
following factors:
 The particular harmonics present in addition to the
fundamental vibration,
 The relative amplitude of each harmonic,
 The transient sounds produced when the vibration is
started.
1st
overtone Fundamental
2nd
overtone
3rd
overtone
resultant
http://surendranath.tripod.com/Harmonics/Harmonics.html

17. Chladni’s Plate
Chladni’s plate is an example of resonance in
a plate.
There are a number of frequencies at which
the plate resonate. Each gives a different
pattern.

18. THANK
YO
U