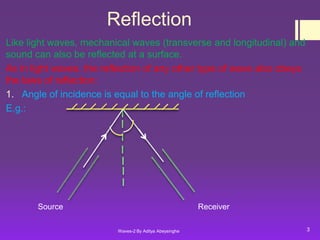
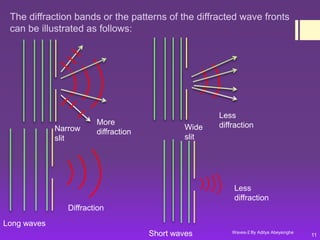
1) The document discusses various properties of waves including reflection, refraction, diffraction, and interference. 2) Reflection of waves follows the law that the angle of incidence equals the angle of reflection. Refraction is caused by changes in wave speed between different mediums and follows Snell's law. 3) Diffraction causes waves to spread out when encountering obstacles. More diffraction occurs with narrow slits and longer wavelengths. 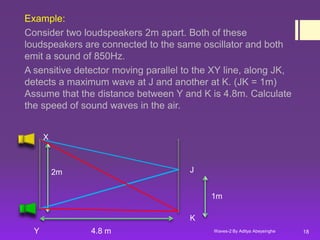4) Interference occurs when two waves overlap. Constructive interference increases amplitude while destructive interference decreases amplitude. Interference patterns can be observed with ripple tanks and sound waves.

1. Waves -2
See more at:

Facebook –
https://www.facebook.com/AdityaAbeysinghePr
esentations

Slideshare - slideshare.net/adityaabeysinghe

Wordpress adityaabeysinghepresentations.wordpress.com/
abeysinghe-foundation/
Waves-2 By Aditya Abeysinghe
1

2. Wave Properties
Waves have various properties. Properties
of waves depend on the type of wave and
the mode of energy transmission.
However, all these characteristics of different
waves can be studied under 4 main topics:
1. Reflection
2. Refraction
3. Diffraction
4. Interference
Waves-2 By Aditya Abeysinghe
2

3. Reflection
Like light waves, mechanical waves (transverse and longitudinal) and
sound can also be reflected at a surface.
As in light waves, the reflection of any other type of wave also obeys
the laws of reflection:
1. Angle of incidence is equal to the angle of reflection
E.g.:
Source
Receiver
Waves-2 By Aditya Abeysinghe
3

4. Sound waves come to a focus when they are incident on a curved
concave mirror.
Also, the sound waves are distributed over large distances when
the sound source is kept on the focus of a curved surface.
E.g.: Loudspeaker
Waves-2 By Aditya Abeysinghe
4

5. Refraction
Before understanding how waves can be refracted
let’s find out how refraction occurs.
Refraction of any source of energy is due to the
change in speed of the waves on entering a different
medium.
E.g.: Sound may propagate on air faster than water
due to various factors, but diffrence in density been
the major factor.
All energy sources that refract off a surface obey the
laws of refraction.
Waves-2 By Aditya Abeysinghe
5

6. Consider the following diagram.
Incident ray
i – incident angle
r – refraction angle
i
Normal
r
Refracted ray
Laws of refraction:
1. The incident and refracted rays, and the normal at the
point of incidence, all lie in the same plane.
2. For two given media, sin i /sinr is a constant. (i is the
angle of incidence and r is the angle of refraction.
Waves-2 By Aditya Abeysinghe
6

7. Examples:
1. The refraction of sound explains why sounds are easier to
hear at night than during day-time.
Day time:
Night time:
Upper layers of the air are colder
than the layers near the ground
level
Upper layers of the air are warmer
than the layers near the ground
level
Ground level
Ground level
Sound waves travel faster the higher the temperature. So,
during the day time the sound waves are refracted away
from the ground level. Thus, the sound intensity decreases.
But, during night, sound waves are refracted towards the
ground level and the intensity of sound increases.
Waves-2 By Aditya Abeysinghe
7

8. 2. Effect of wind on sound
Consider two occasions when,
(i) The wind is blowing in the direction of sound.
wind
Sound
Source
Observer
Here the bottom of the sound
wavefront is moving more slowly
than the upper part. So, the
wavefront turns towards the observer
(O). So, the sound is heard easily.
(ii) The wind is blowing away from the direction of the sound.
Sound
wind
Source
Observer
Here the upper part of the sound
wavefront is moving more slowly
than the bottom part. So, the
wavefront turns away from the
observer (O). So, the sound intensity
diminishes.
Waves-2 By Aditya Abeysinghe
8

9. Diffraction
Diffraction occurs when any type of wave meets an
obstacle. The behavior of waves on facing an
obstacle varies depending on the size of the
obstacle.
When the size of the aperture in the obstacle
incresase, there is less pressure on that aperture,
so the wave maintains a low diffraction pattern
beyond the obstacle and viceversa.
Diffraction can be clearly observed using a ripple
tank.
Waves-2 By Aditya Abeysinghe
9

10. Ripple tank -
Waves-2 By Aditya Abeysinghe
10

11. The diffraction bands or the patterns of the diffracted wave fronts
can be illustrated as follows:
Narrow
slit
More
diffraction
Wide
slit
Less
diffraction
Less
diffraction
Diffraction
Long waves
Short waves
Waves-2 By Aditya Abeysinghe
11

12. The reason for such a variation in the wave
patterns is due to the change in wavelength.
Generally, the smaller the width of the aperture
in relation to the wavelength, the greater is the
diffraction.
A similar effect can be observed when sound
waves are diffracted at a surface. Diffraction
increases with longer wavelength.
By the inverse relationship between the
frequency (f) and the wave length (λ), it is clear
as to why sounds with high frequency defract
less.
Waves-2 By Aditya Abeysinghe
12

13. Interference
When two or more waves of the same frequency overlap,
interference occurs.
Interference can be easily explained using the theory of
superposition.
Consider the diagram below.
If the two
A
B
Waves-2 By Aditya Abeysinghe
oscillators are in
phase, crests from
A will meet crests
from B and troughs
from B will meet
troughs from B.
Similarly when the
two oscillators are
not in phase,
troughs/crests
from A will meet
crests/troughs
from B.
13

14. waves.
Applying the Principle of superposition
Consider two occasions:
(i) When the two waves are in phase
(ii) When the two waves are not in phase
Waves-2 By Aditya Abeysinghe
14

15. When the two waves are in phase
Crests from wave A will meet
crests from Wave B and troughs
from wave A will meet troughs from
wave B.
This process increases the
amplitude of the resultant wave.
Thus, this process is called the
constructive interference
A
Trough
Trough
When the two waves are not in phase
Crest
Crest
B
Waves-2 By Aditya Abeysinghe
Trough
Crests from wave A will meet
troughs from Wave B and troughs
from wave A will meet crests from
wave B.
This process decreases the
amplitude of the resultant wave.
Thus, this process is called the
destructive interference
15

16. Now consider what happens when two oscillators are placed and
activated on a ripple tank.
A bright spot can be observed due to the increase of the amplitude
of the resultant wave. Thus, white bands are due to constructive
interference.
Similarly, dark spot can be observed due to the decrease of the
amplitude of the resultant wave. Thus, dark bands are due to the
destructive interference.
Waves-2 By Aditya Abeysinghe
16

17. Interference of sound wavesConsider the following diagram.
X
Destructive interference
Constructive interference
Destructive interference
Constructive interference
Destructive interference
As the ear or
microphone is moved
along the line XY, a
larger or a smaller
sound is heard
depending on the
type of interference
(constructive or
destructive)
Constructive interference
Destructive interference
Y
Waves-2 By Aditya Abeysinghe
17

18. Example:
Consider two loudspeakers 2m apart. Both of these
loudspeakers are connected to the same oscillator and both
emit a sound of 850Hz.
A sensitive detector moving parallel to the XY line, along JK,
detects a maximum wave at J and another at K. (JK = 1m)
Assume that the distance between Y and K is 4.8m. Calculate
the speed of sound waves in the air.
X
J
2m
1m
K
Y
4.8 m
Waves-2 By Aditya Abeysinghe
18

19. Since both at J and at K, sound can be heard, J and K can be
considered to be points of constructive interference. Furthermore,
XJ = YJ.
Since, K is the next point at which a sound was heard,
XK – YK = λ
(λ is the wavelength)
XK can be found using the Pythagoras theorem,
XK = √ XY2 + YK2 = 5.2 m
Therefore, λ = XK – YK = 5.2m – 4.8m = 0.4m
Thus, the velocity of sound on air,
V = fλ
V = 850 × 0.4 = 340 ms-1
19
Waves-2 By Aditya Abeysinghe