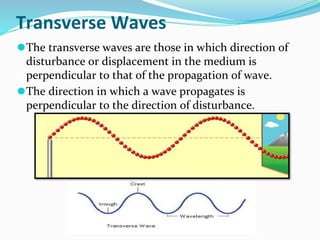
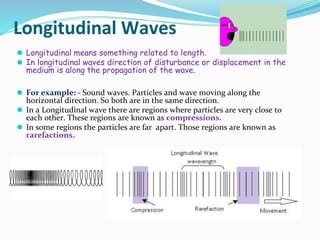
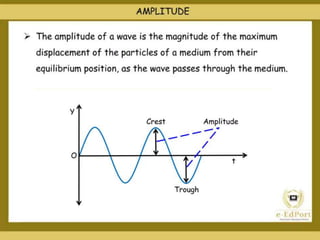
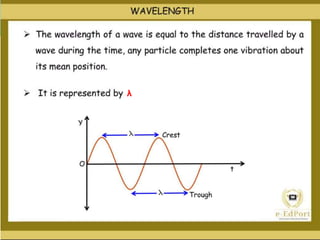
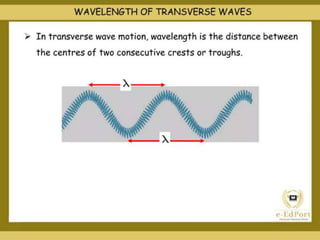
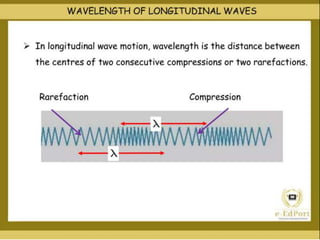
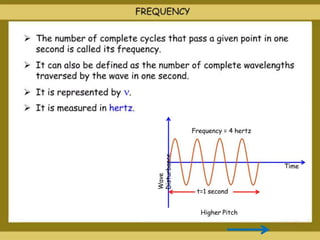
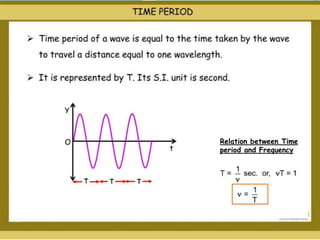
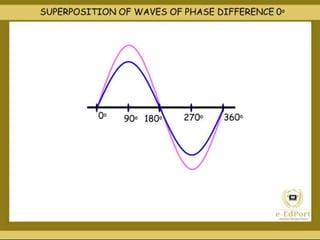
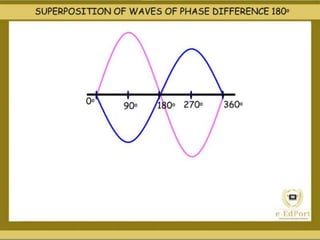
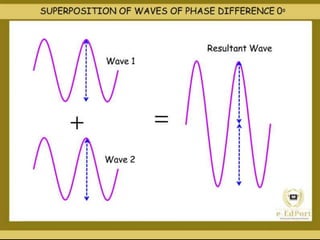
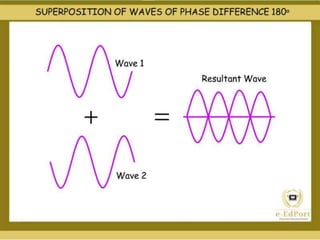
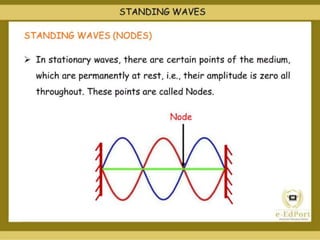
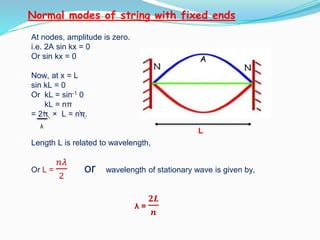
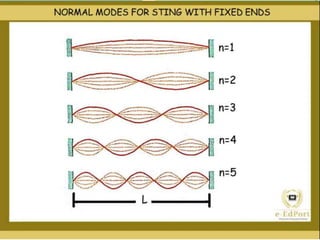
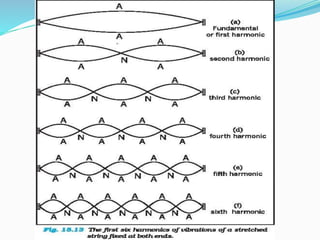
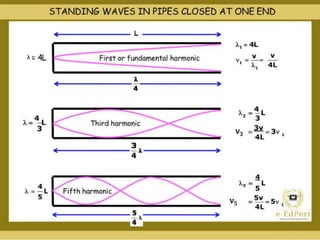
The document discusses the concept of waves, explaining their nature as disturbances that propagate energy through a medium without the net movement of particles. It outlines different types of waves including mechanical, electromagnetic, and matter waves, and details properties such as transverse and longitudinal waves, as well as standing waves. The document also covers harmonic frequencies and the equations related to wave characteristics and behaviors in mediums such as strings and organ pipes.

1. WAVES

2. What is a wave?
For example: -
⚫ Consider the sound of the horn; this sound reaches our ear
because of sound waves.
⚫ There is transfer of energy from one point to another with
the help of particles in the medium.
⚫ These particles don’t move they just move around their mean
position, but the energy is getting transferred from one
particle to another and it keeps on transferring till it
reaches the destination.
A wave is a disturbance that propagates through
space, that carries energy without the net movement
of particles.

3. Types of Waves
⚫ Mechanical waves
⚫ Electromagnetic waves
⚫ Matter waves
⚫ Mechanical waves: -
⚫ The mechanical waves are governed by all the Newton’s laws of
motion.
⚫ Medium is needed for propagation of the wave.
⚫ For Example: - Water Waves, Sound Waves

4. Transverse Waves
⚫The transverse waves are those in which direction of
disturbance or displacement in the medium is
perpendicular to that of the propagation of wave.
⚫The direction in which a wave propagates is
perpendicular to the direction of disturbance.

5. Longitudinal Waves
⚫ Longitudinal means something related to length.
⚫ In longitudinal waves direction of disturbance or displacement in the
medium is along the propagation of the wave.
⚫ For example: - Sound waves. Particles and wave moving along the
horizontal direction. So both are in the same direction.
⚫ In a Longitudinal wave there are regions where particles are very close to
each other. These regions are known as compressions.
⚫ In some regions the particles are far apart. Those regions are known as
rarefactions.

8. λ

11. It represents the phase change per unit path.
WAVE NUMBER
It is the number of waves present in unit distance of a medium.

14. Relation between Time
period and Frequency

15. Displacement relation for a plane progressive wave

16. y(x, t) = a sin (kx + ωt + φ )
(Positive x-axis)
(Negative x-axis)

28. Relation between wave velocity, frequency
and wavelength of a wave

32. Equation for a standing wave
 Here, amplitude of the wave is 2A sin kx

33. The position of antinodes will be at points where,
sin kx = ± 1
i.e. kx = sin-1 (1)
i.e. kx = ( n +
1
2
) π , where n = 0,1,2,3……
(Since, ( n +
1
2
) π multiples of π will give maximum values of sin function.
i.e. 1)
2π
λ
x = ( n +
1
2
) π Now, bringing
2π
λ
to the RHS and taking ½ outside
the bracket, we get:
x = ( n +
1
2
) π .
λ
2π
Or x = ( 2n + 1)
λ
4
Or x =
λ
4
,
3λ
4
,
5λ
4
,………
These positions of maximum amplitudes are called antinodes. Clearly, the
separation between two consecutive nodes is
λ
2
.

34. The position of nodes will be at points where,
sin kx = 0 or kx = nπ, where n = 0,1,2…..
On solving we get x = n
𝝀
𝟐
or x = 0,
λ
2
,λ,
3λ
2
, ……….
These positions of zero amplitudes are called nodes.

35. Standing waves in a String
Consider a string clamped to rigid supports at its ends. If the wire be plucked in the
middle, transverse waves will travel along it and gets reflected from the ends. These
identical waves travelling in opposite directions give rise to stationary waves.
The string vibrates in segments or loops with certain natural frequencies. These
special patterns are called normal modes.
Equation of a standing wave,
y = 2A sin kx cos ωt, where 2A sin kx is the amplitude of the wave.

36. At nodes, amplitude is zero.
i.e. 2A sin kx = 0
Or sin kx = 0
Now, at x = L
sin kL = 0
Or kL = sin-1 0
kL = nπ
= 2π × L = nπ.
Length L is related to wavelength,
Or L =
𝑛𝜆
2
or wavelength of stationary wave is given by,
λ =
𝟐𝑳
𝒏
λ
L
Normal modes of string with fixed ends

37. • For n = 3  L =
3𝜆
2
and ν3 =3 ×
𝐯
𝟐𝑳
== ν=3 ν1
This frequency is called third Harmonic or second overtone and so
on.
The corresponding frequency is given by, ν =
𝐯
λ
ν =
𝐯
λ
=
𝒏𝐯
𝟐𝑳
• For n = 1, ν1 =
𝐯
𝟐𝑳
also L =
𝝀
𝟐
The lowest possible natural frequency of a system is called its fundamental
mode(note) or the first harmonic. For the stretched string fixed at either
end it is given by , ν1 =
𝒗
𝟐𝑳
corresponding to n = 1
• For n = 2  L = λ and ν2 =2 ×
𝐯
𝟐𝑳
== ν=2 ν1
This frequency is called second harmonic or first overtone.

42. Equation of a standing wave,
y = 2A sin kx cos ωt, where
2A sin kx is the amplitude of the
wave.

43. The position of nodes will be at points where,
sin kx = 0 or kx = nπ, where n = 0,1,2…..
On solving we get x = n
𝝀
𝟐
or x = 0,
λ
2
,λ,
3λ
2
, ……….
These positions of zero amplitudes are called nodes.
The positions of nodes in a closed organ pipe

44. The position of antinodes will be at points where,
sin kx = ± 1
i.e. kx = sin-1 (1)
i.e. kx = ( n +
1
2
) π , where n = 0,1,2,3……
2π
λ
x = ( n +
1
2
) π Now, bringing
2π
λ
to the RHS, we get:
x = ( n +
1
2
) π .
λ
2π
Now, x = L = ( n +
𝟏
𝟐
)
𝝀
𝟐
,where n = 0, 1,2,3….
Or x =
λ
4
,
3λ
4
,
5λ
4
,………
These positions of maximum amplitudes are called antinodes.
The corresponding frequency is given by, ν =
𝐯
λ

45. So, ν3 = 3 ν1
ν3
ν1
Or third harmonic, for n = 1
Fundamental frequency
L = ( n +
𝟏
𝟐
)
𝝀
𝟐
𝑺𝒐, At n=0

46. In an organ pipe closed at one end, it is found that the
higher frequencies are odd harmonics.
ν5
So, ν5 = 5 ν1
Similarly for n = 2, the corresponding frequency is fifth
harmonic or second overtone and so on.

47. λ
ν3
ν5

48. Normal Modes of vibration of an open organ pipe
(i) First mode of vibration:
L = λ/2 or λ = 2L
Frequency of vibration,
ν1 = v /2L ---- Fundamental note or first harmonic
(ii) Second mode of vibration:
L = λ
Frequency,
ν2 = v / L = 2 ν1 -----First overtone or second harmonic
Similarly,
ν3 = 3 ν1 ---2nd overtone / 3rd harmonic
ν4 = 4 ν1
ν5 = 5 ν1
---3nd overtone / 4th harmonic
---4nd overtone / 5th harmonic