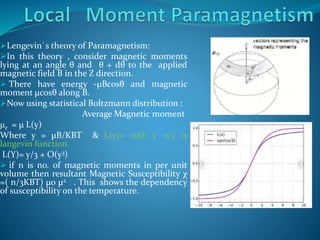
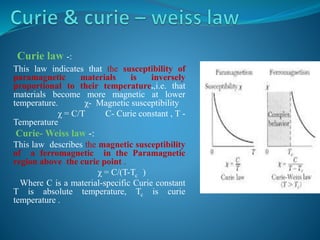
This document discusses different types of paramagnetism. It defines paramagnetism as having a positive magnetic susceptibility and being able to align with an applied magnetic field. Paramagnetism can originate from unpaired electrons or conduction electrons in metals. The document then covers Lengevin's classical theory of paramagnetism, Curie and Curie-Weiss laws, Pauli paramagnetism from conduction electrons, and the crossover between localized moment behavior and Pauli paramagnetism.

1. Instructor :- Dr. Soumik mukhoupadhyay
Name:-Vishnu Kumar Tiwari
Roll. No.:- 181171
Email- tvishnu@iitk.ac.in

2. 1.Definition of Paramagnetism
2. Different Origion of Paramagnetism
3.Local Moment Paramagnetism
4. Effective Magnetic moment
5.Van Velck Paramagnetism
6.Curie & Curie-Weiss law
7. Pauli Paramagnetism
8.Crossover between local moment
Paramagnetism and Pauli Paramagetism

3. Definition of Paramagnetism
 Positive Susceptibility( χ >0)
 An applied magnetic field Induces a magnetization which
aligns parallel with the applied magnetic field which caused
it.
 Non zero Magnetic moment(M) because of unpaired
electrons lined up in direction of magnetic field.
 Without magnetic field(B= 0): M=0 because of random
orientation of unpaired electrons.
 An increase of magnetic field will tend
to line up spins, an increase of temperature
will randomize them. So magnetization is
depend on ratio (BT).
(B=0)
(B>0)

4. The peramagnet magnetic moment results from the
following cotributions:
The spin and intrinsic moments of the electrons.
 The Orbital motion of electron .
The spin magnetic moment of nucleolus.
Paramagnetism observed in metals because of odd no. of
electrons.
Paramagnetism can be explained by classical theory which
is known is Lengevin`s theory of Paramagnetism.

5. Lengevin`s theory of Paramagnetism:
In this theory , consider magnetic moments
lying at an angle θ and θ + dθ to the applied
magnetic field B in the Z direction.
 There have energy -μBcosθ and magnetic
moment μcosθ along B.
Now using statistical Boltzmann distribution :
Average Magnetic moment
μz = μ L(y)
Where y = μB/KBT & L(y)= coth y -1/y is
langevin function.
L(Y)= y/3 + O(y3)
 if n is no. of magnetic moments in per unit
volume then resultant Magnetic Susceptibility χ
=( n/3KBT) μ0 μ2 . This shows the dependency
of susceptibility on the temperature.

6. In general, magnetization M =Ms Bj(y)
Where saturation magnetization Ms = ngj μBJ
Where Bj(y) = Brillouin function
By solving this ,susceptibility χ=(n/3kB T)μ◦ μeff
2
 μeff is effective magnetic moment = gj μB
[J(J+1)]1/2
 where Lande gj value = (3/2) + S(S+1) –L(L+1)
2J(J+1)
 Using hund`s rules application, For 4f
elements, effective magnetic moment value closed
to experimental value .
 3d elements experimental effective magnetic
moment are not agree with this theoretical value
because of Orbital quenching it means orbital
angular momentum is quenched (L=0).

7. If j=0 in the ground state, there is ground state energy
shifts
This term is
positive because of
En >E0 . And is
called Van Vleck
paramagnetism
This terms is
negative ,is the
diamagnetism
susceptibility Both are small and
temperature independt

8. Curie law -:
This law indicates that the susceptibility of
paramagnetic materials is inversely
proportional to their temperature.,i.e. that
materials become more magnetic at lower
temperature. χ- Magnetic susceptibility
χ = C/T C- Curie constant , T -
Temperature
Curie- Weiss law -:
This law describes the magnetic susceptibility
of a ferromagnetic in the Paramagnetic
region above the curie point .
χ = C/(T-Tc )
Where C is a material-specific Curie constant
T is absolute temperature, Tc is curie
temperature .

9. In metal each spin either up or
down. When magnetic field is
applied then energy of electron
is raised and lowered depending
on its spin .
State of electron with parellel
(antiparellel) to B have higher
(lower) energy with respect to
the state with zero magetic field.
 Energy parabola splits in to
two which are separated by 2
μBB shown in figure .

10. Magnetization M= μB(n+ - n-)
n+ or n- no. of electron per unit volume with spin parallel(+)
or antiparellel(-) with respect to the external magnetic field B.
n+ =1/2g(EF)μBB
n- = -1/2g(EF)μBB
M = g(EF)μB
2B
Pauli susceptibility χp = μ◦g(EF)μB
2
g(EF )= 3/2(n/EF )
This expression is temperature independent and very small .
 This paramagnetism shows by metal due to conduction
electrons.

11.  The effect of the Fermi Dirac statistics and the croos over Pauli
paramagnetism between localized moment behavior can be illustrated by
rederiving .
n+ =1/2ʃg(E+μBB)f(E)dE
 n- = 1/2ʃg(E-μBB)f(E)dE
Now Magnetization M = μB (n+ - n- )
Now solving this using Taylor expansion,
 M= μB
2 Bʃ(-df/dE)g(E)dE
In the degenerate limit at T=0, M = μB
2 Bg(EF ) & χp = μ◦g(EF)μB
2
In the nondegenrate limit f(E) =exp[-(E- μ)/k B T] so by solving this :
 M = n μB
2 B/K B T & χp = nμ◦μB
2 /K B T
 This susceptibility equalnt to n localized moments (of magnitude μB )
per unit volume .

12.  Thank you