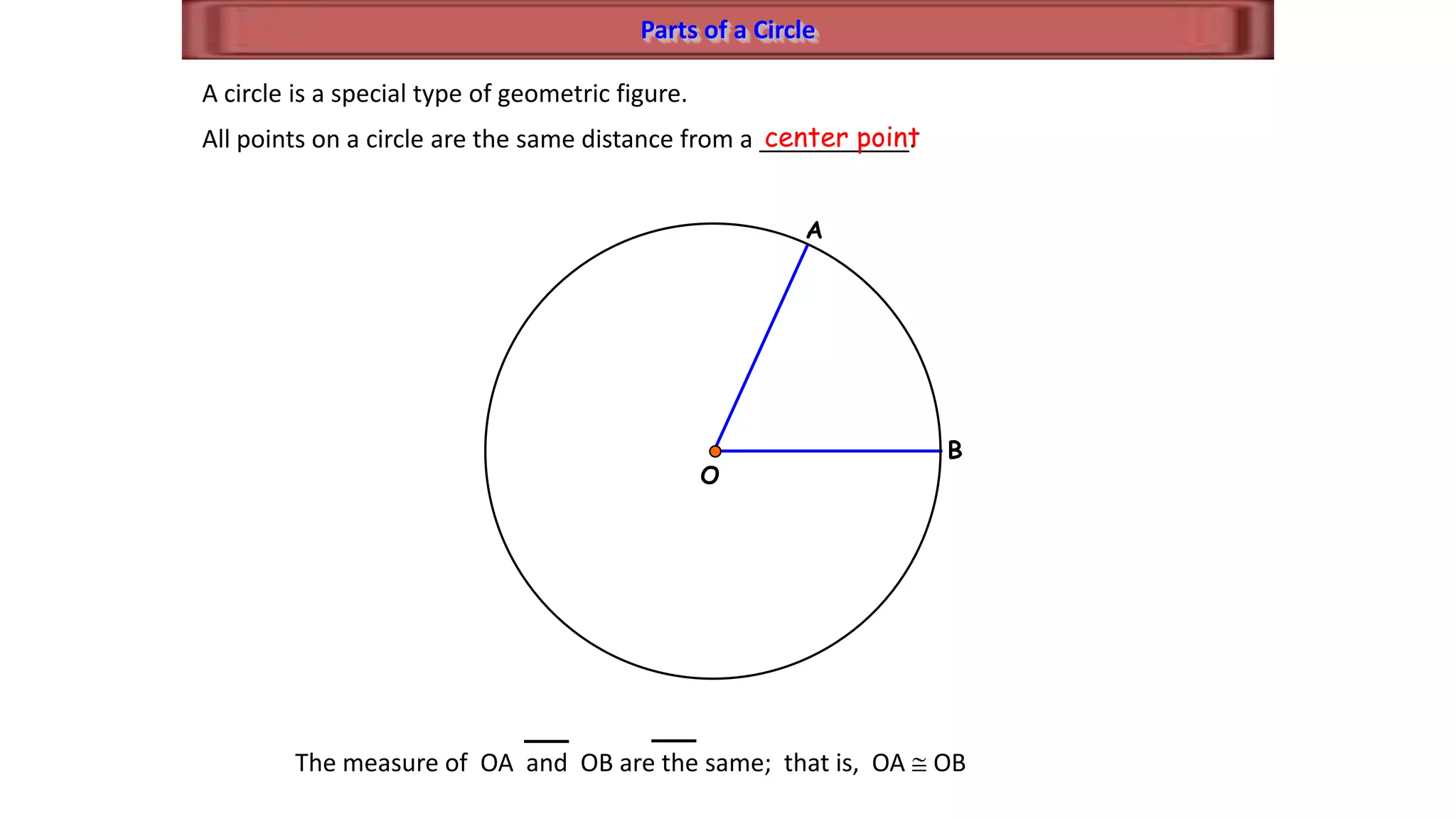
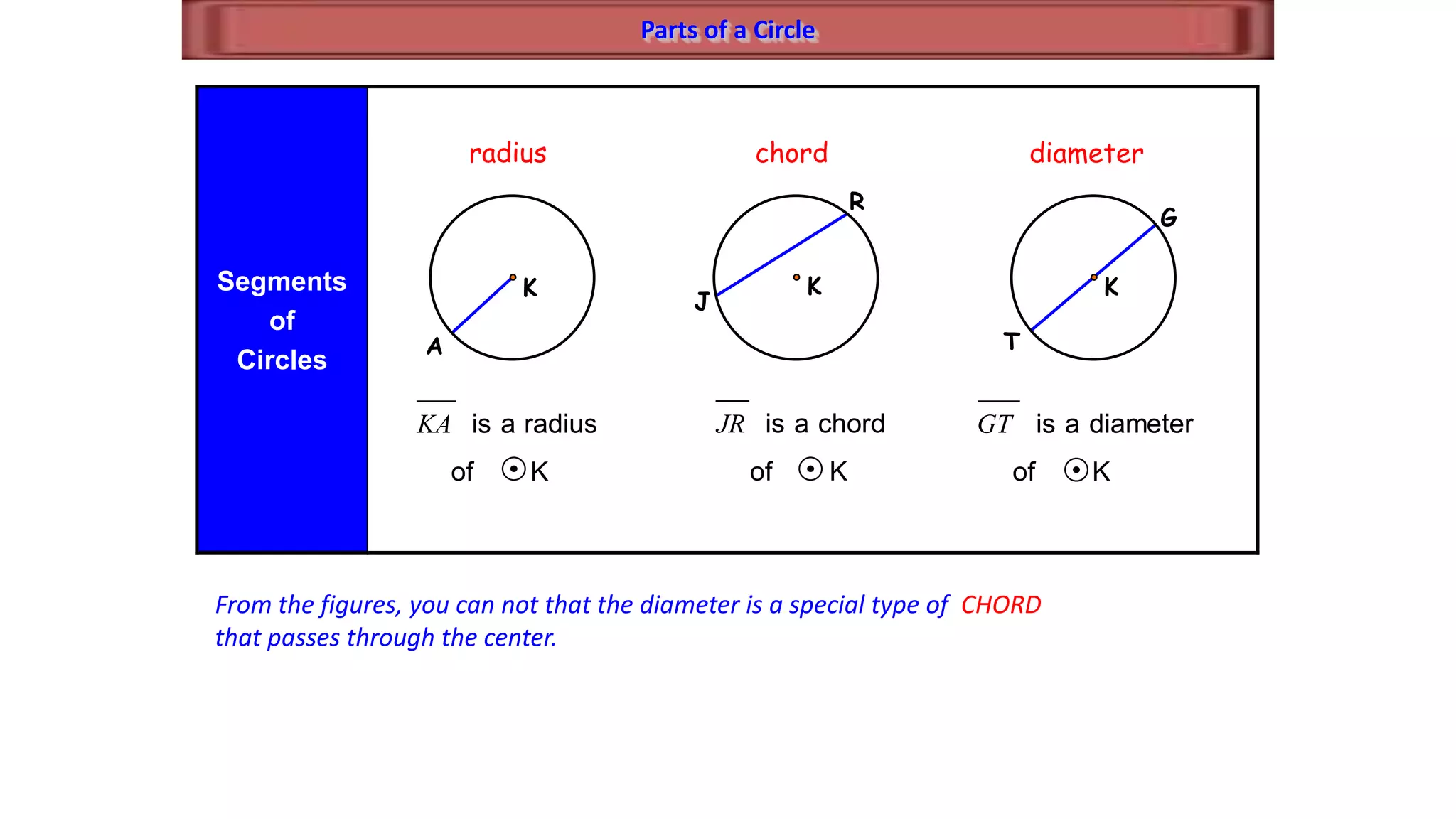
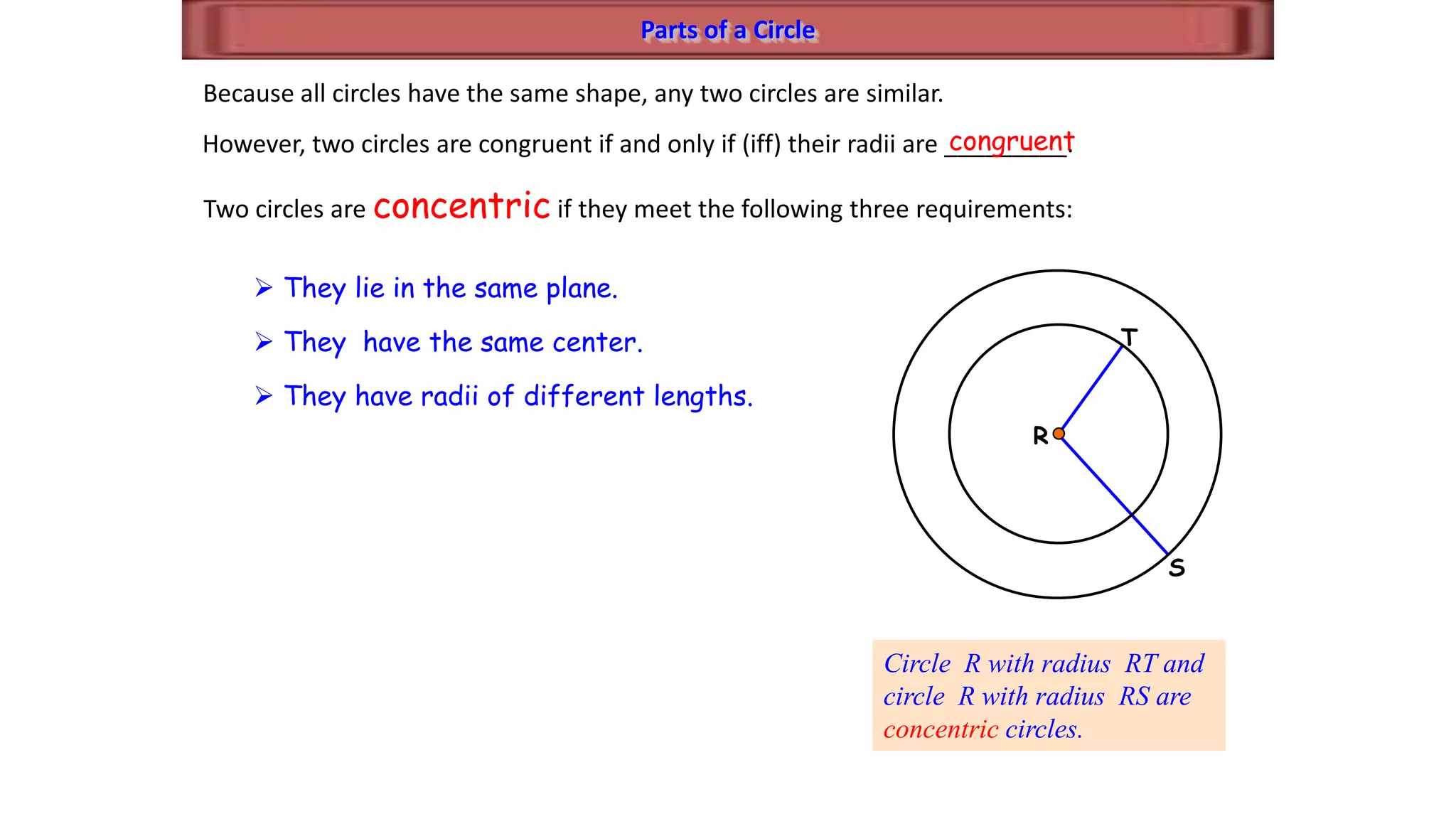
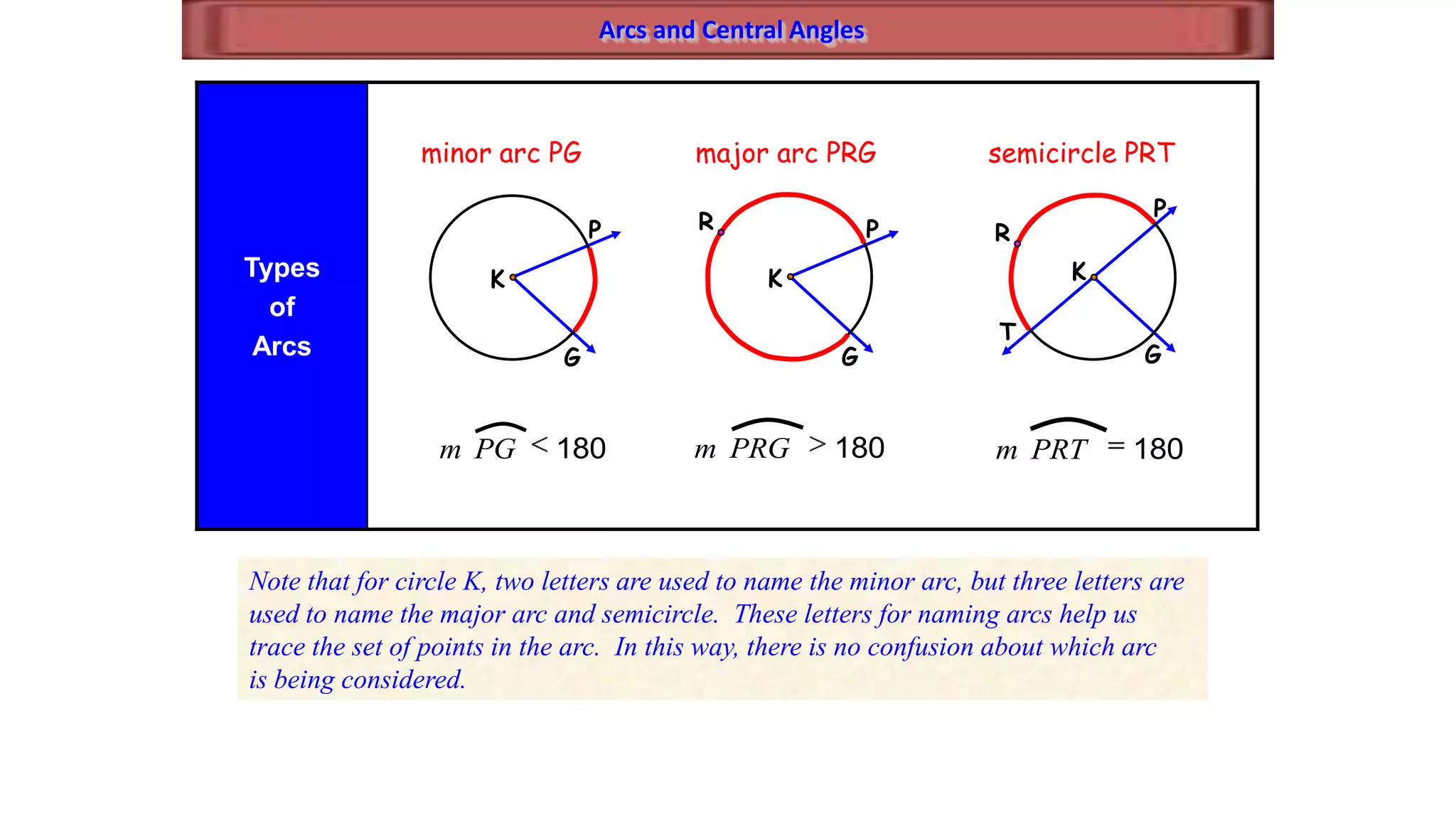
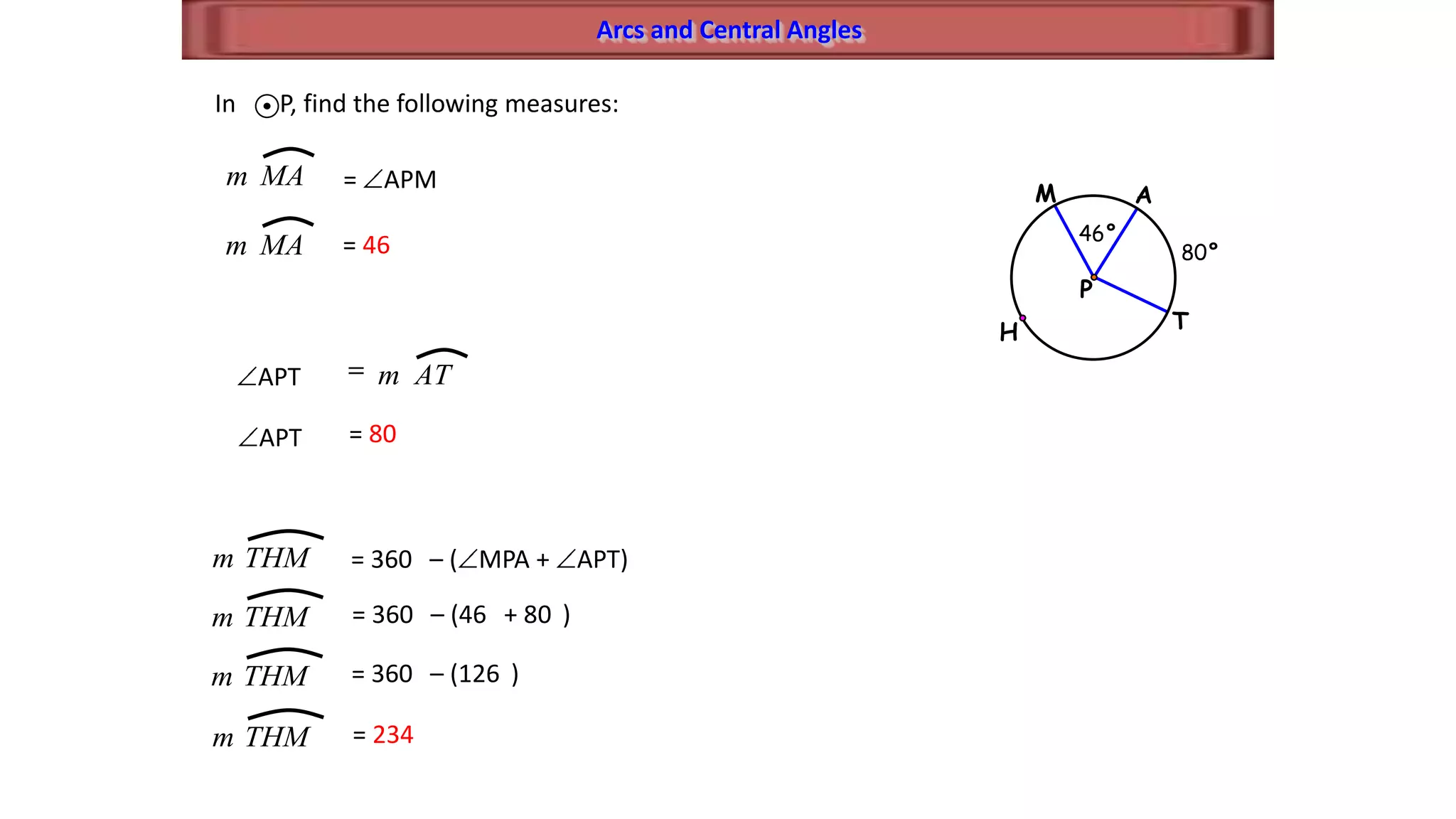
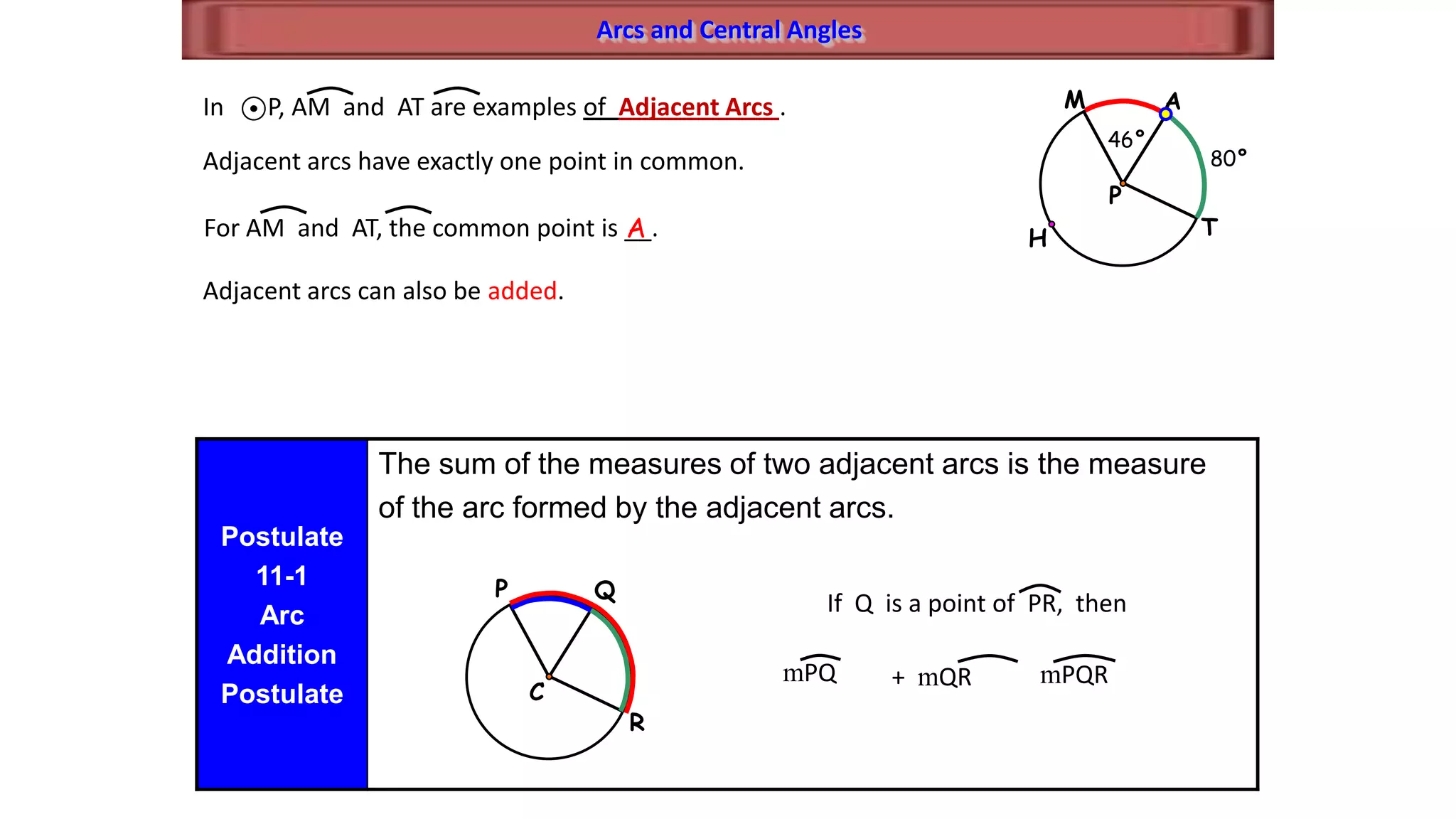
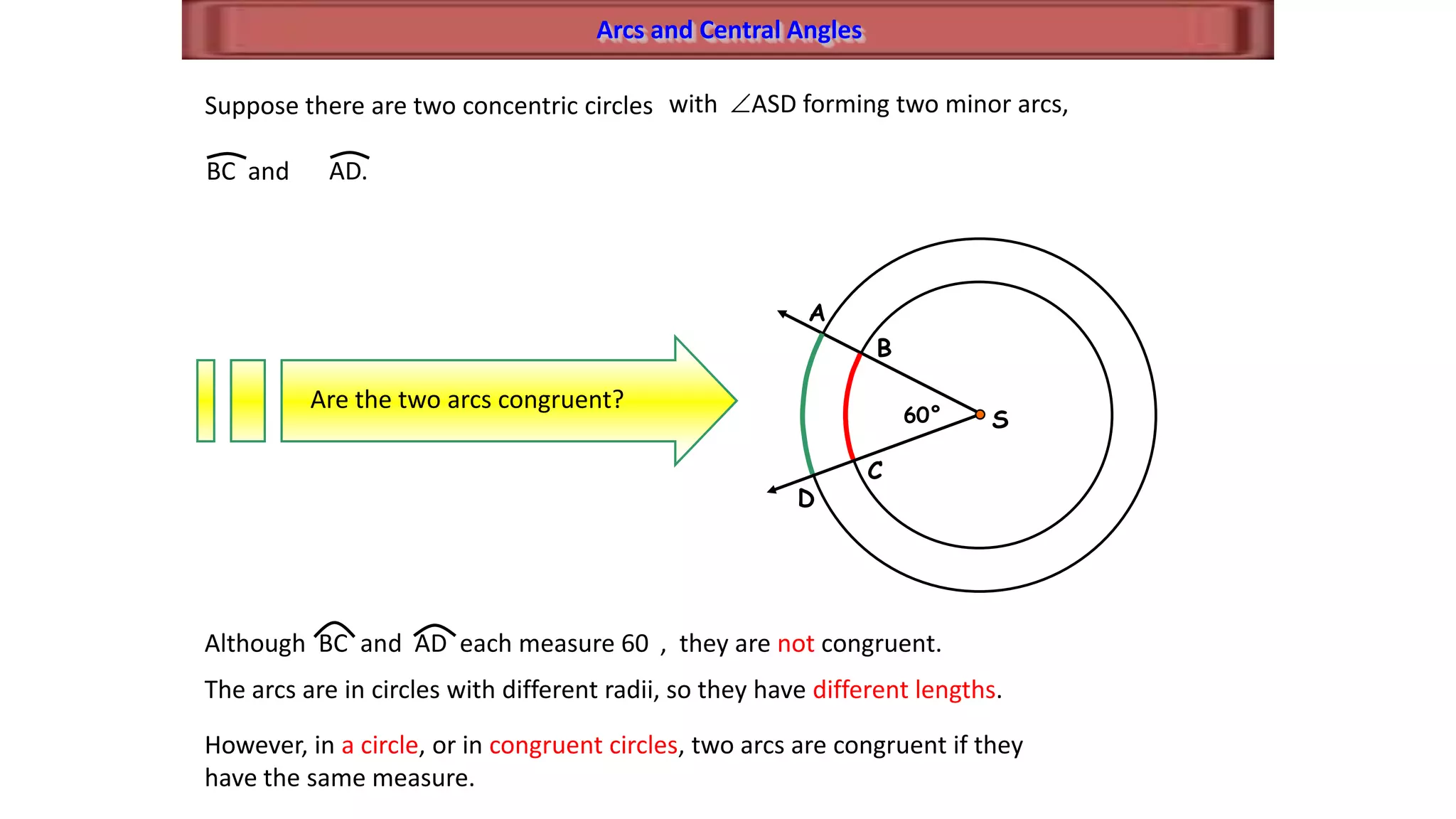
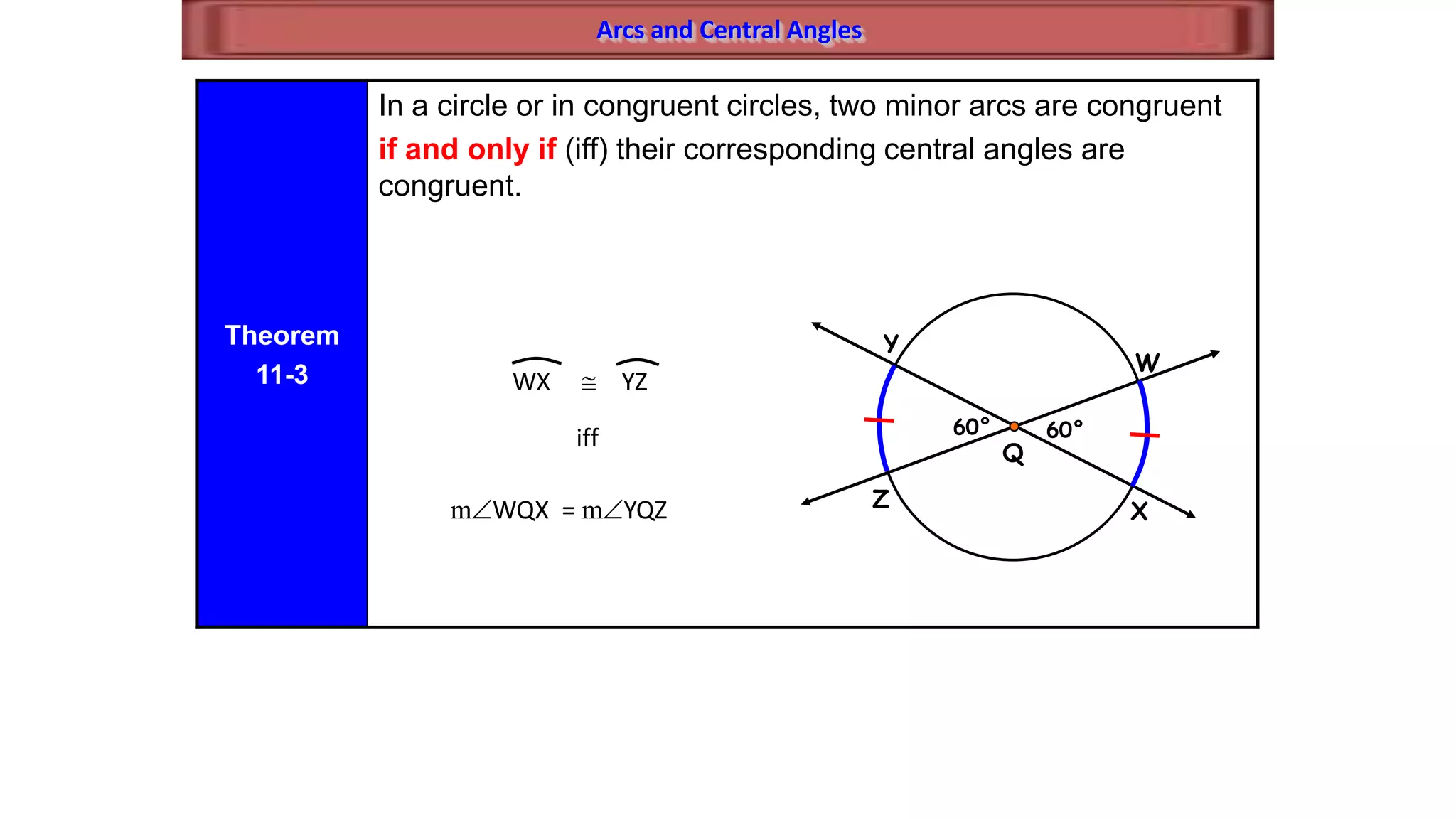
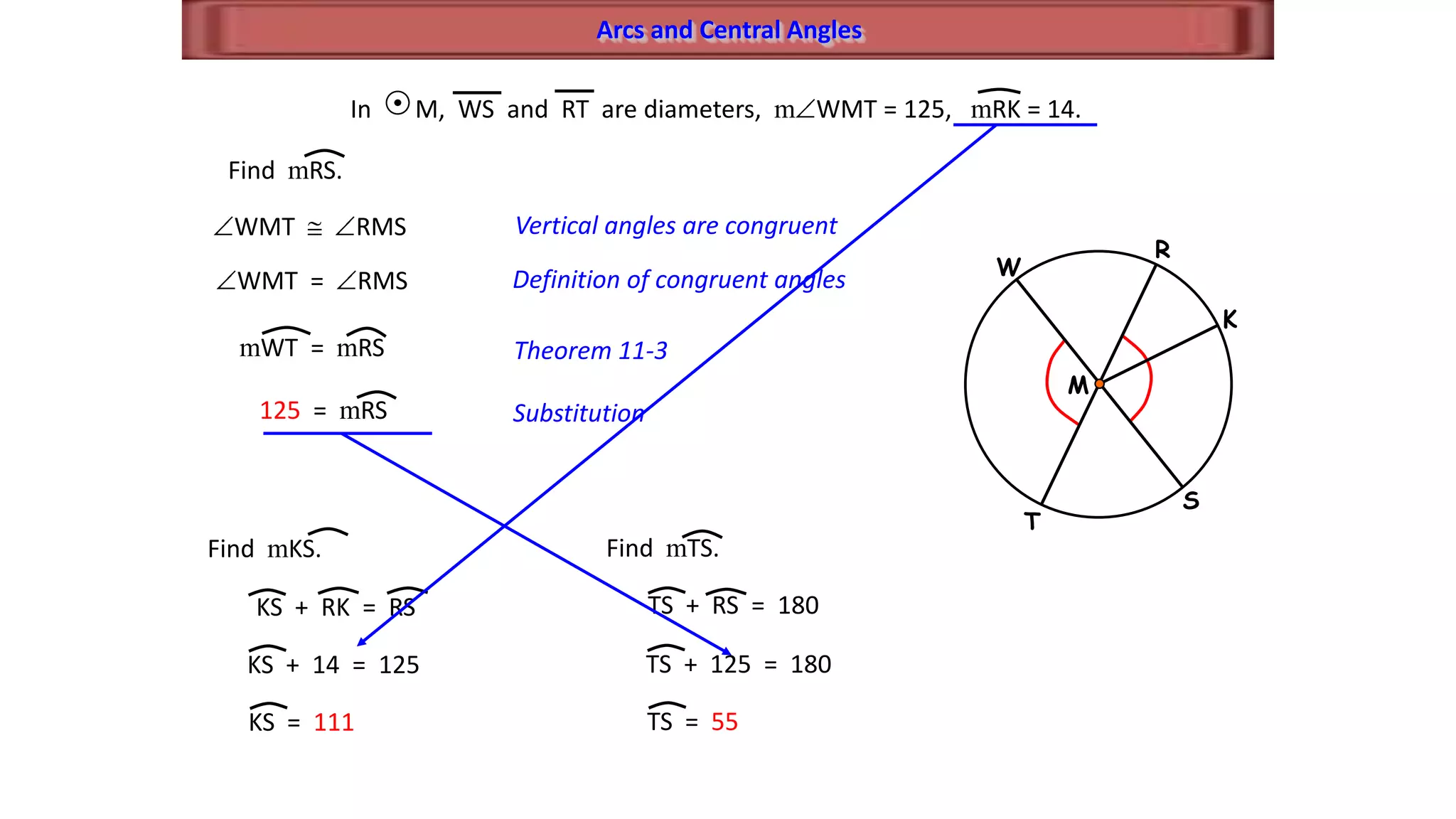
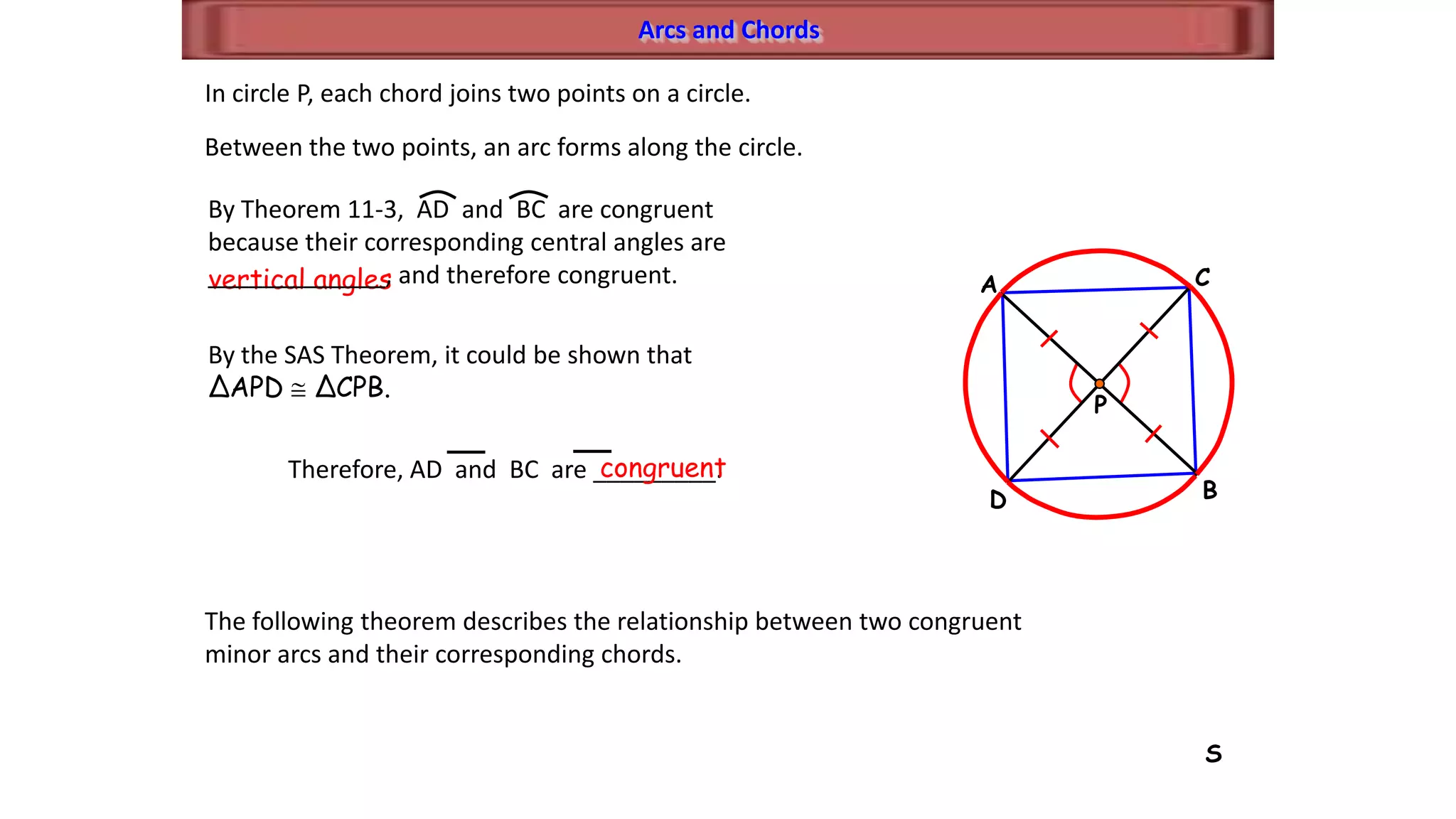
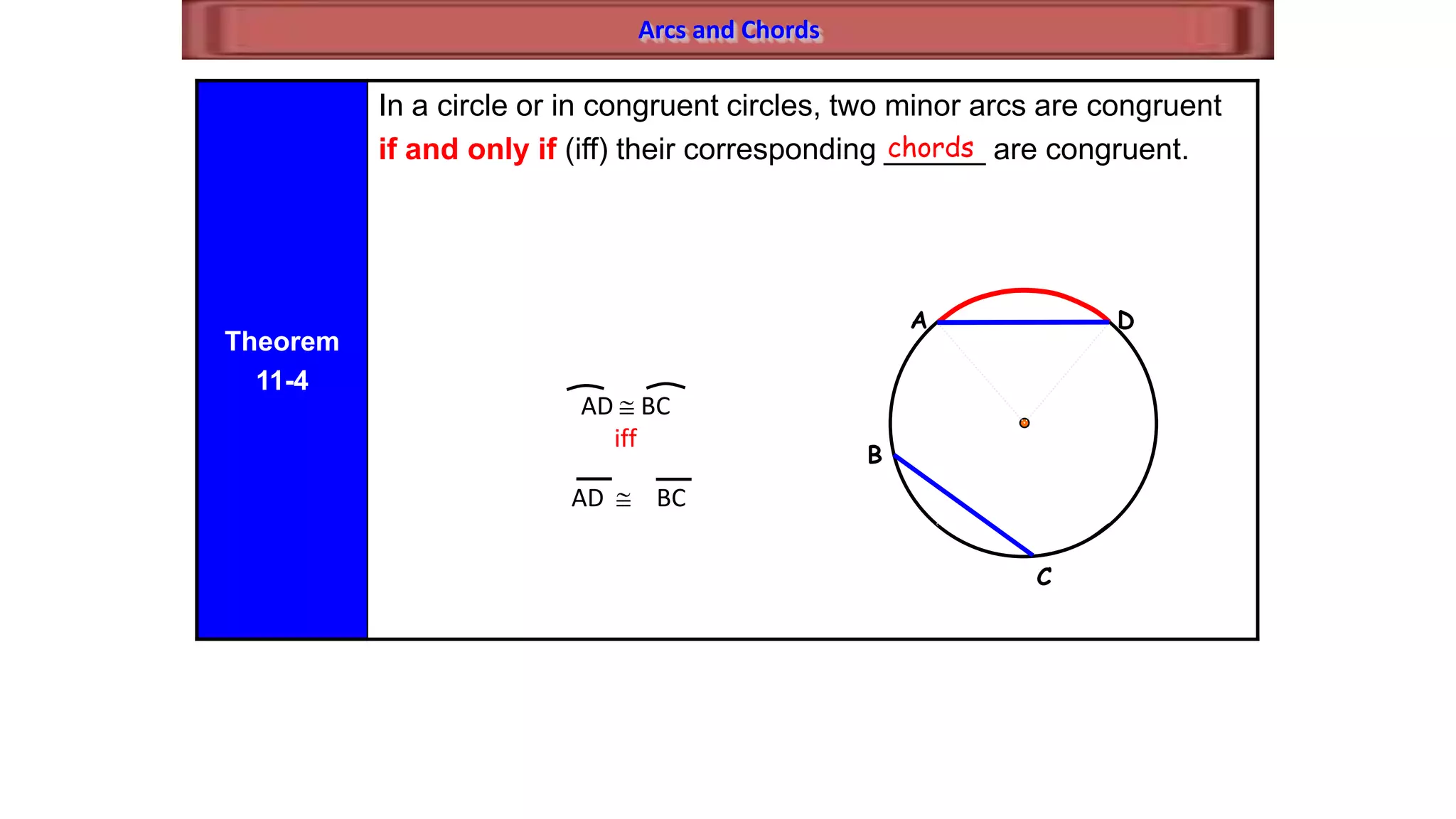
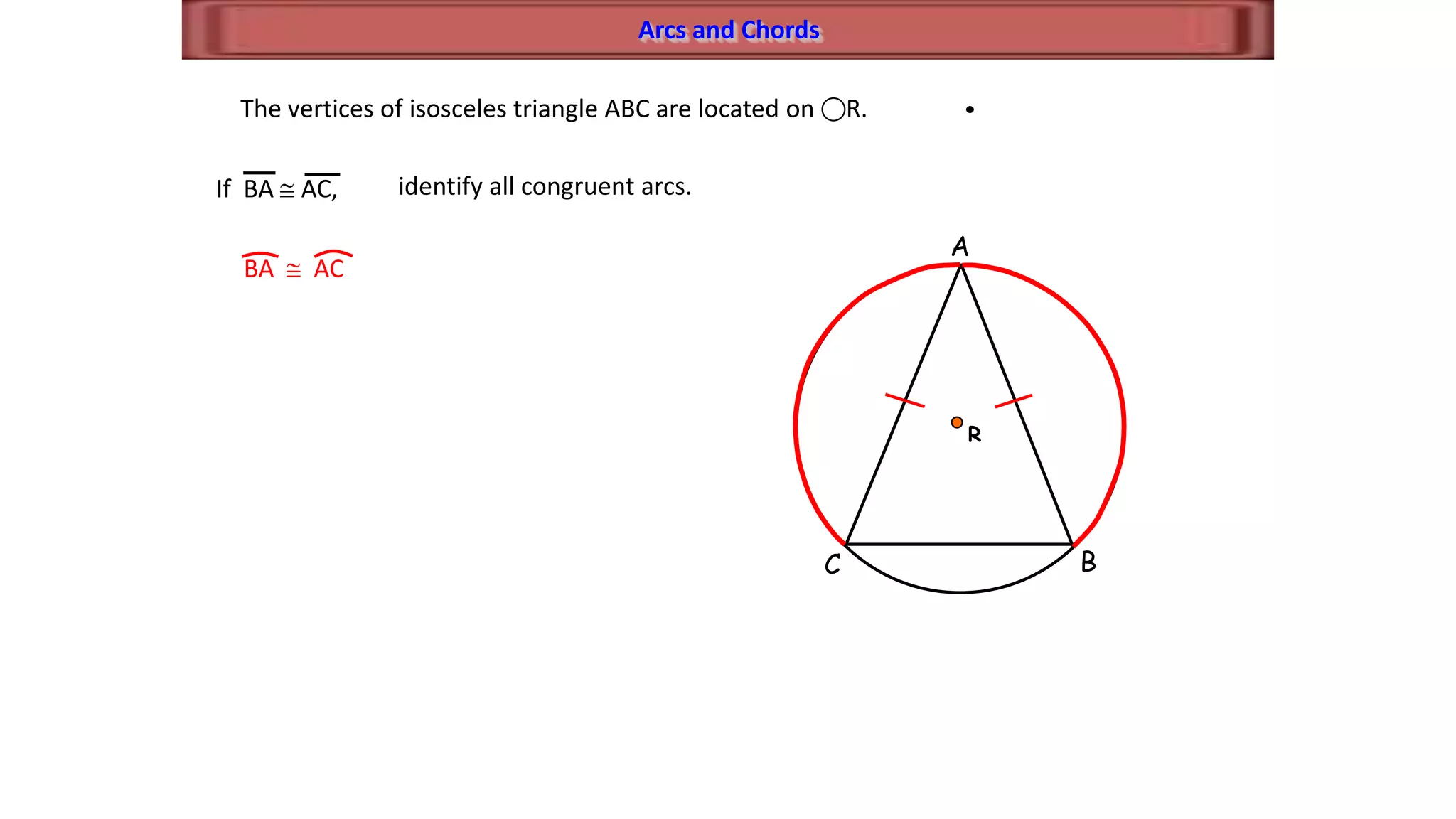
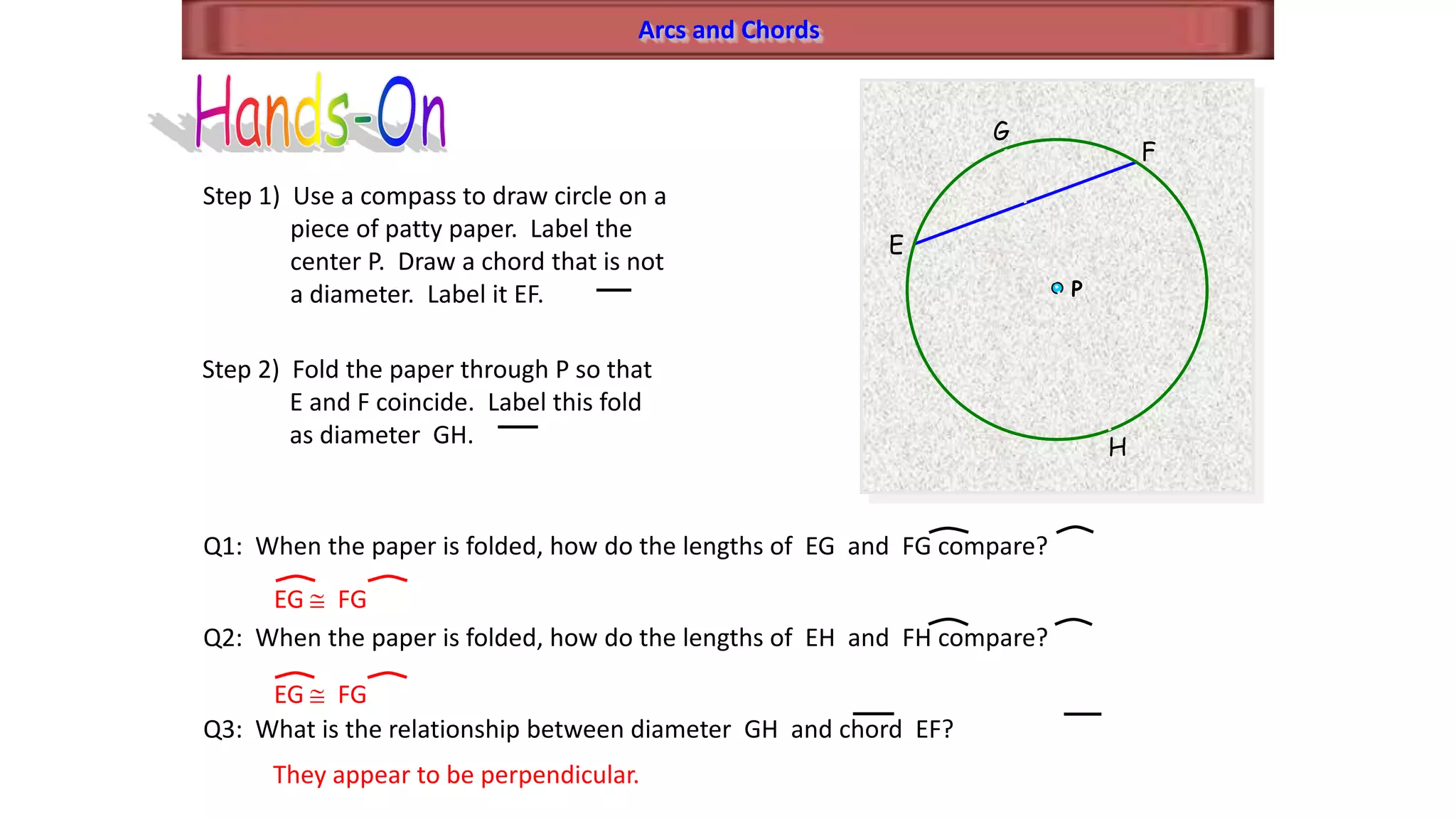
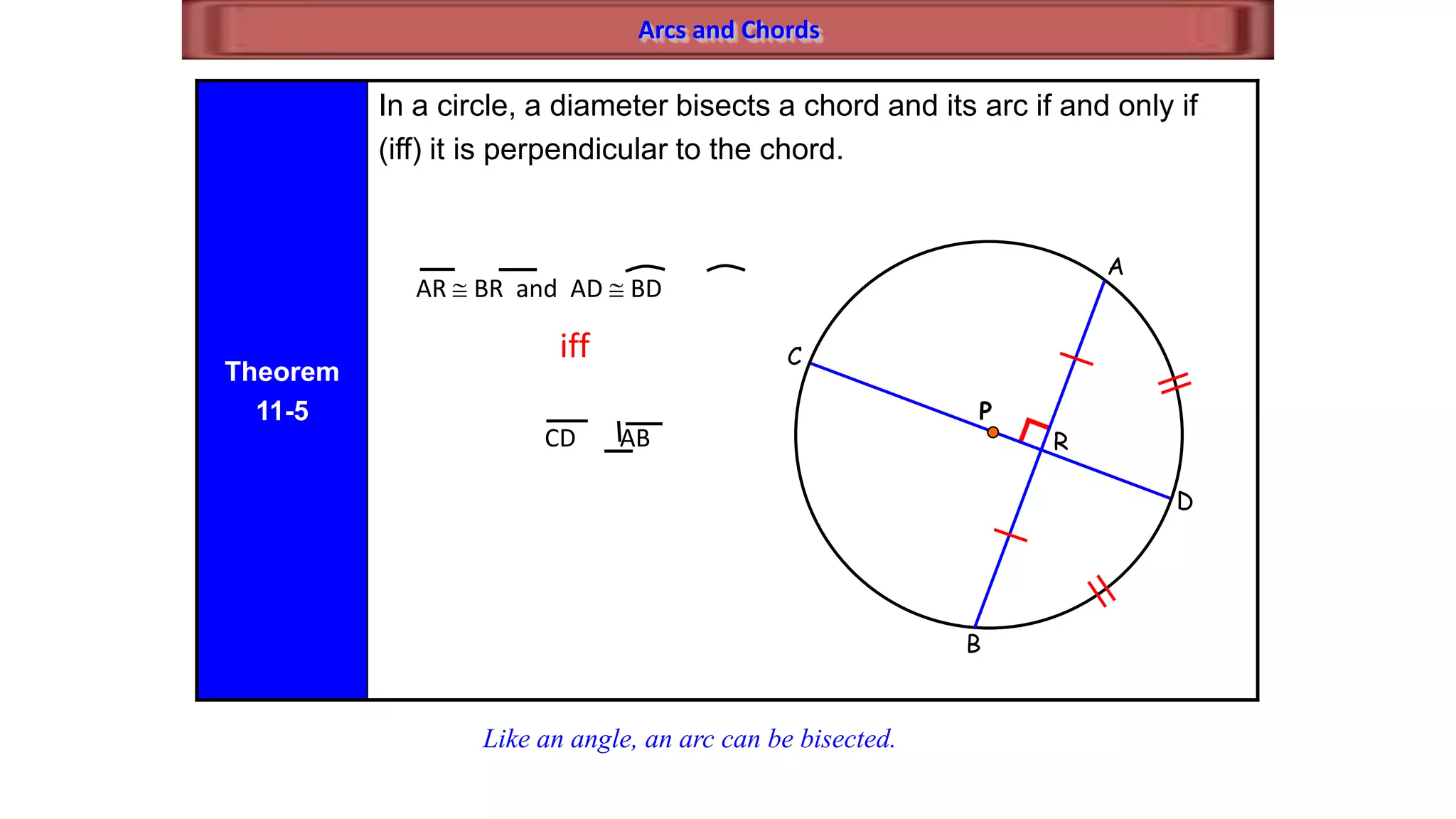
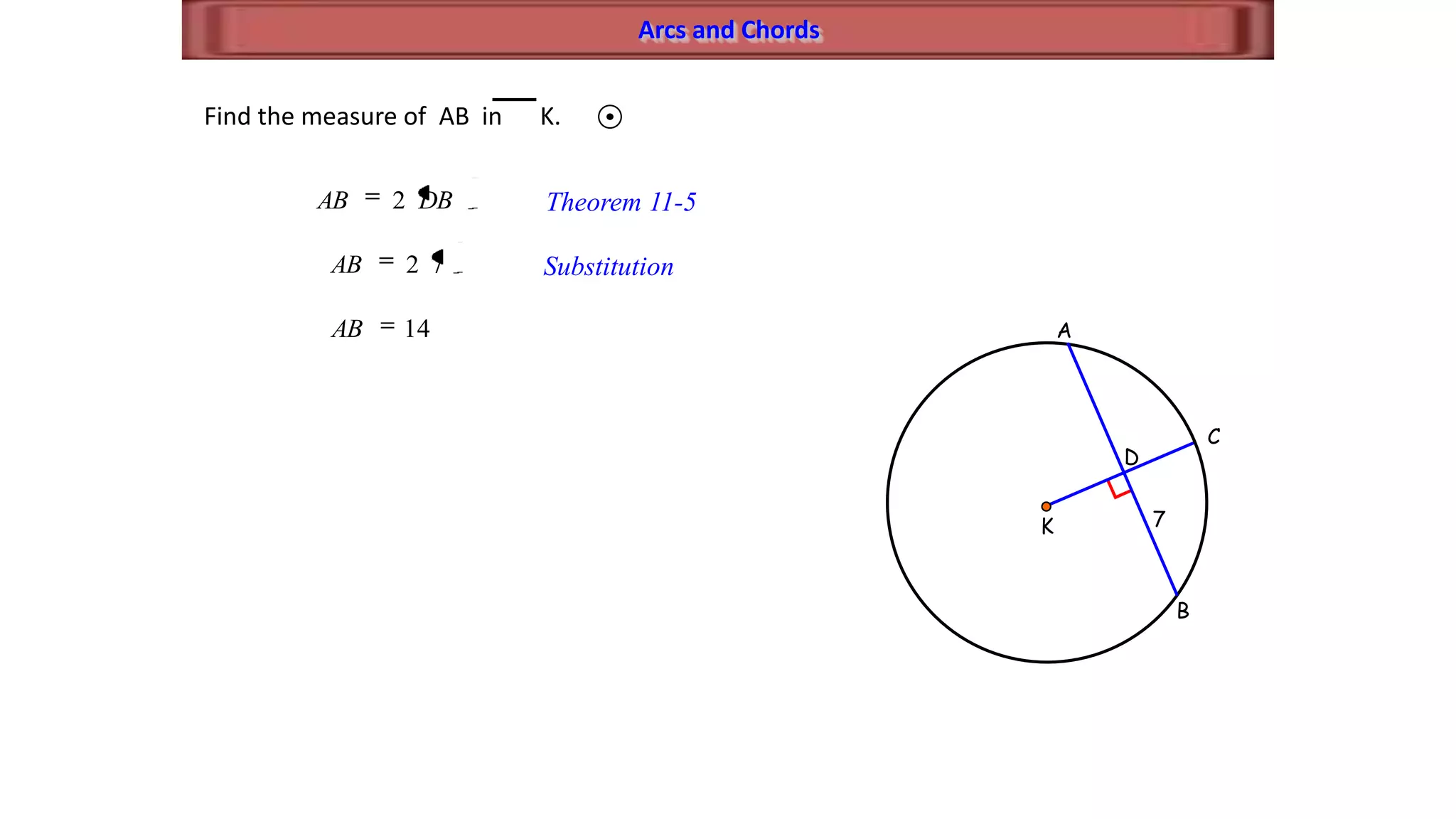
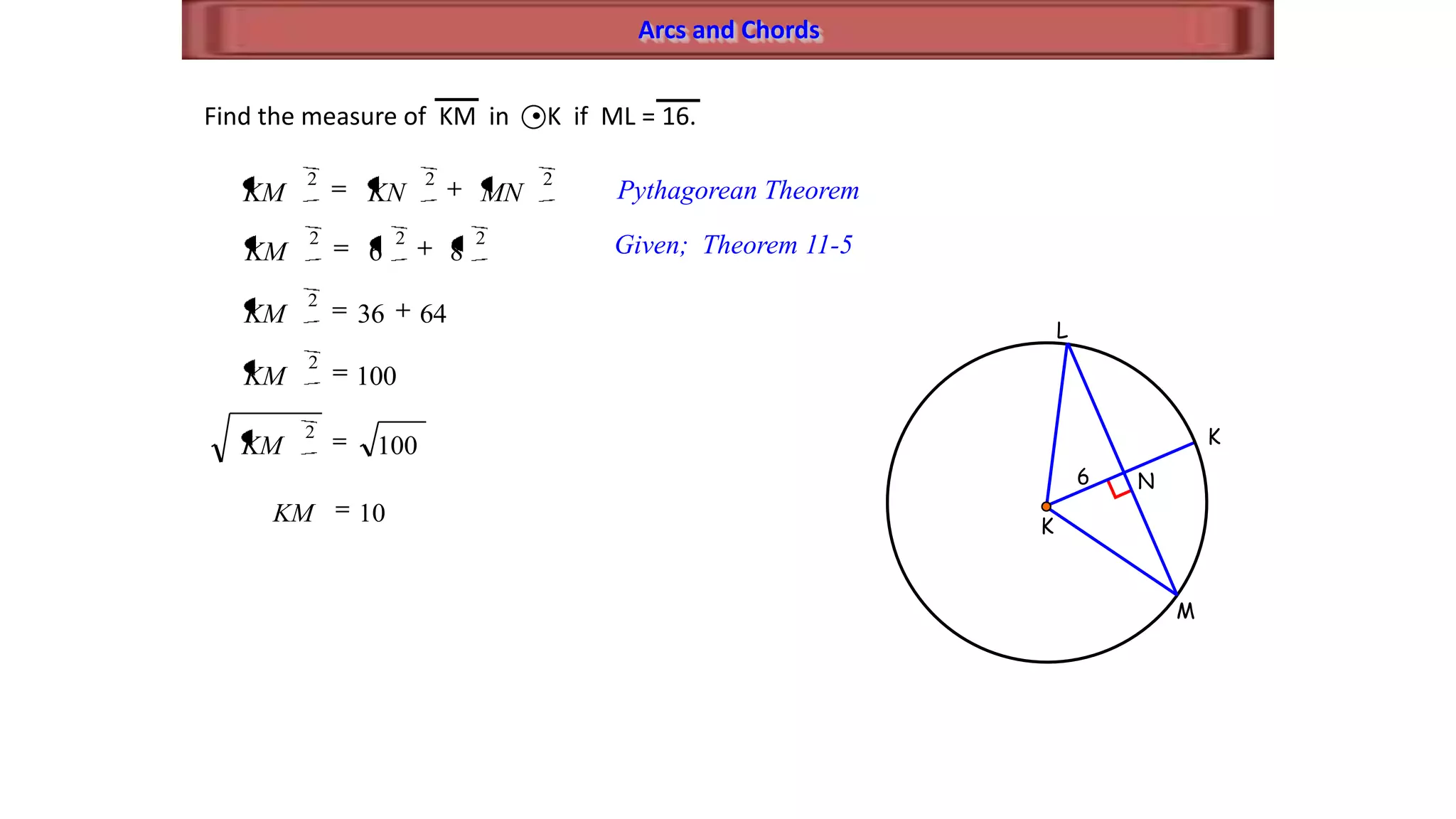
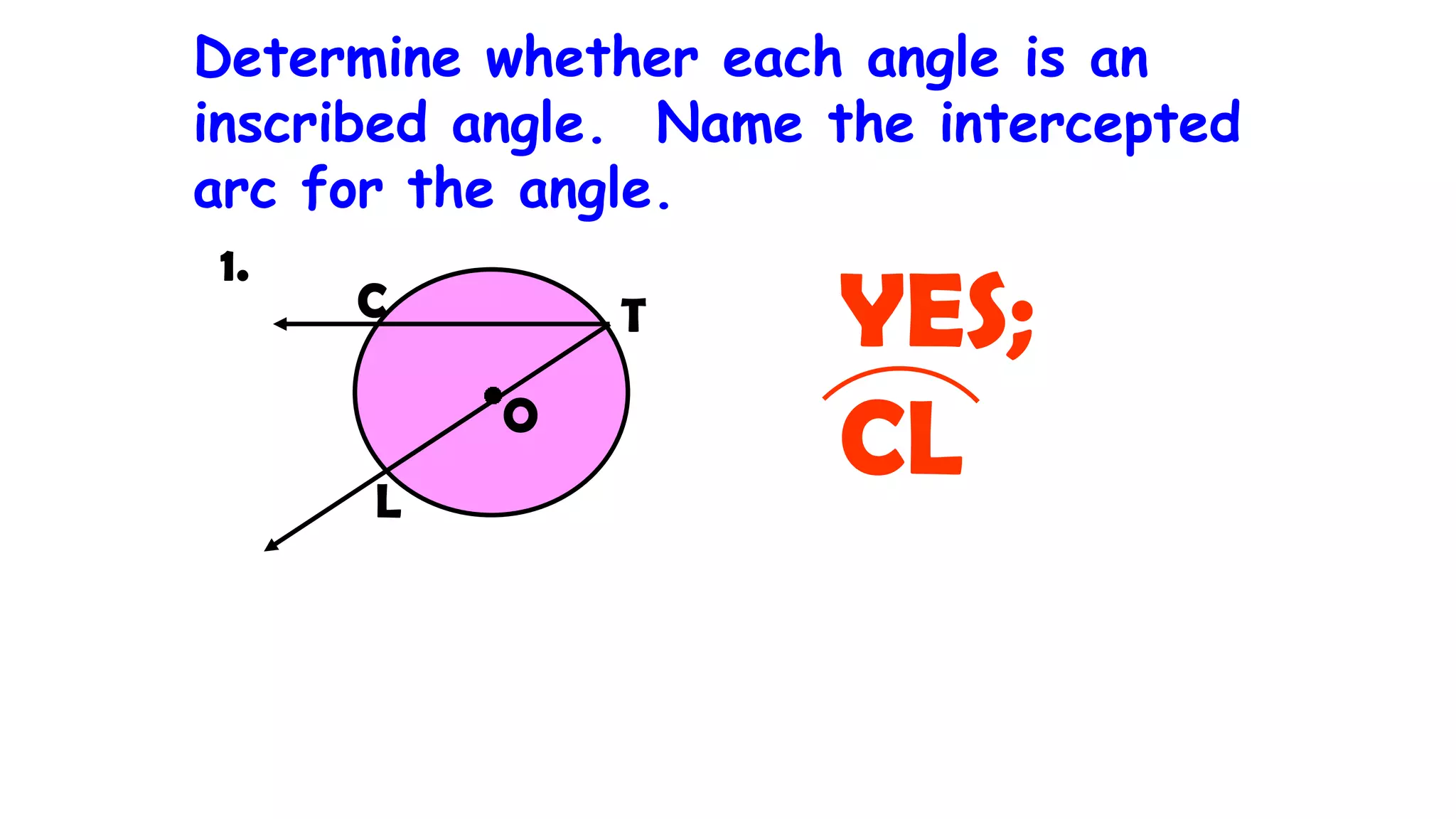
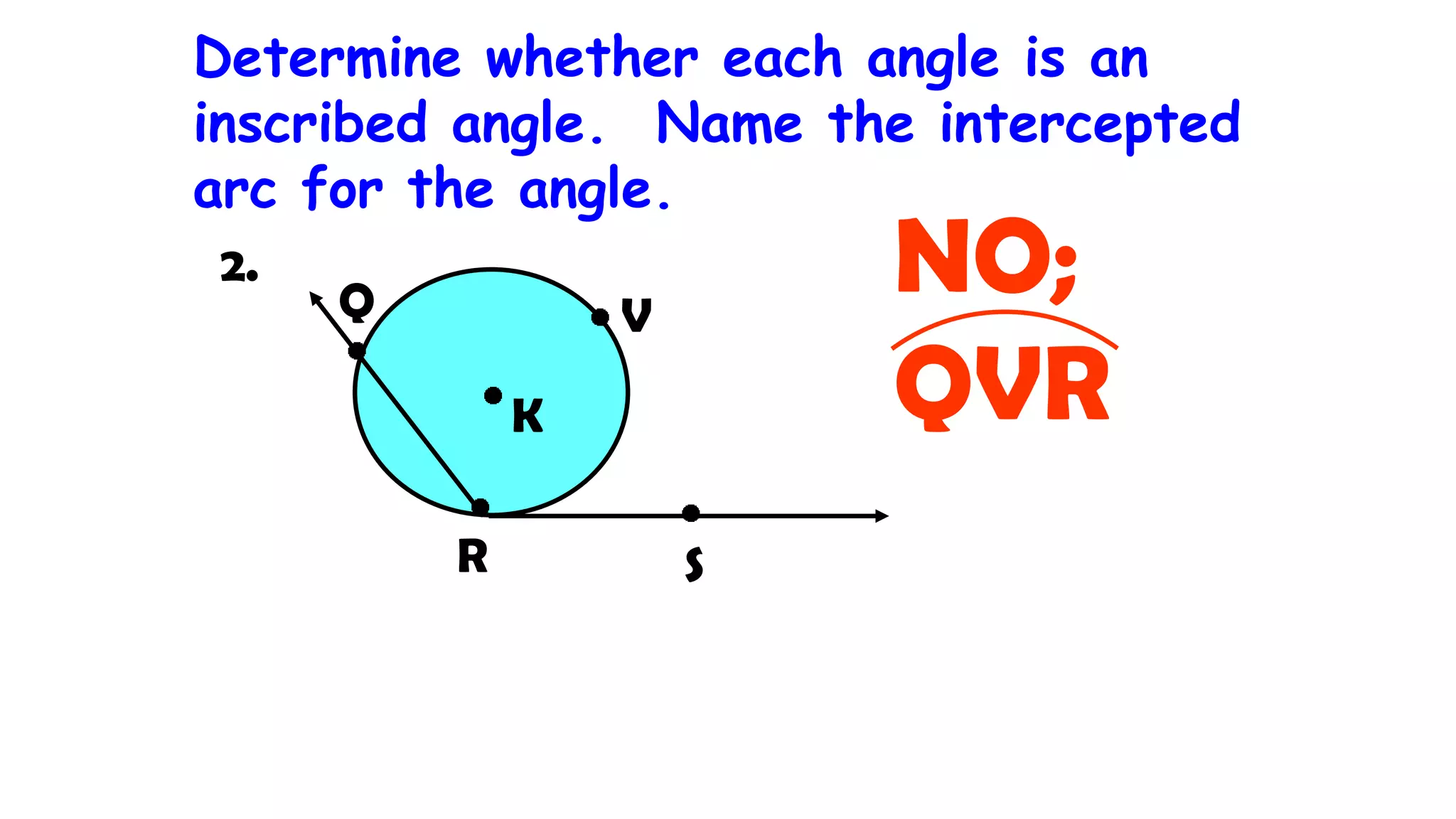
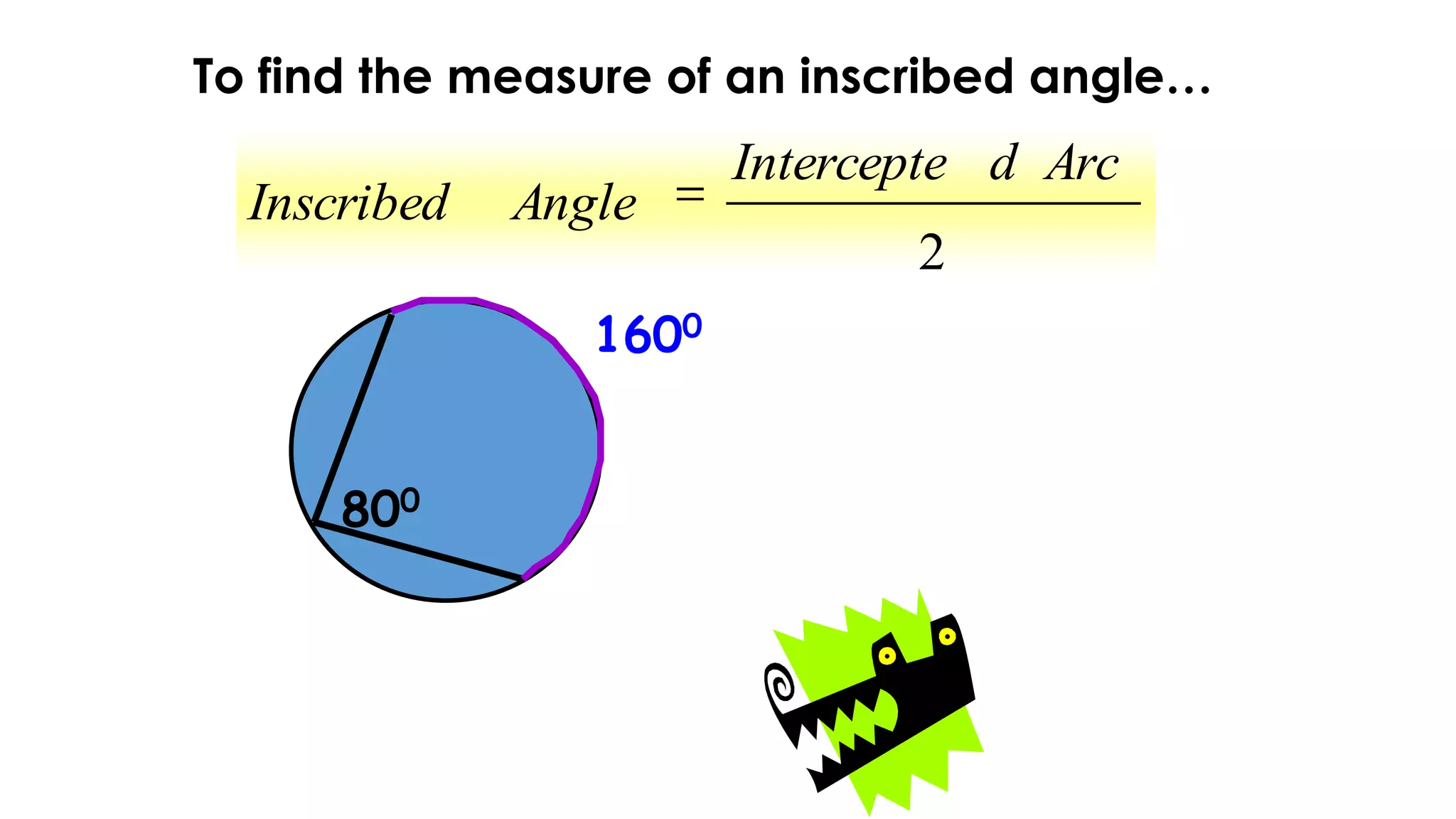
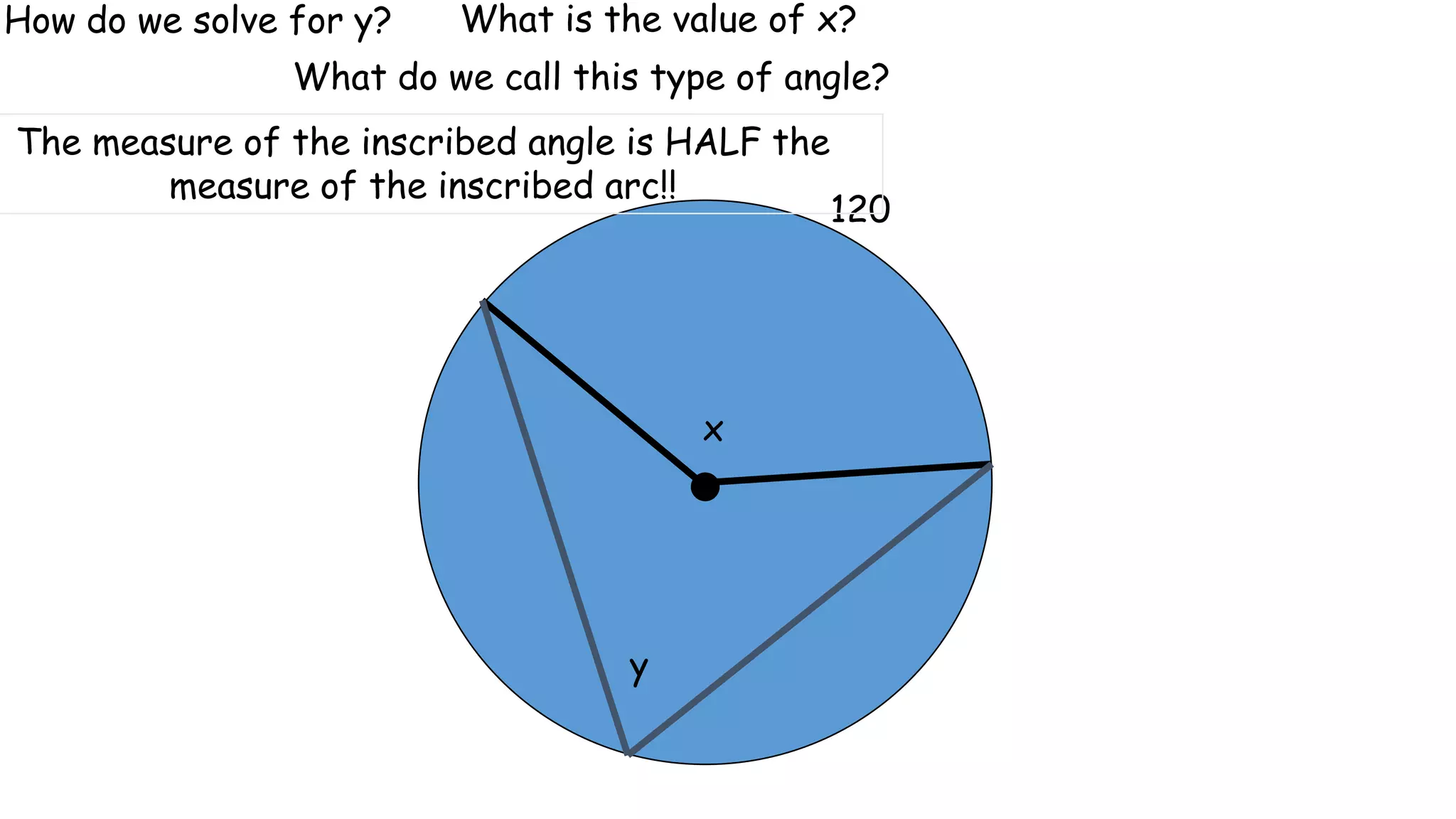
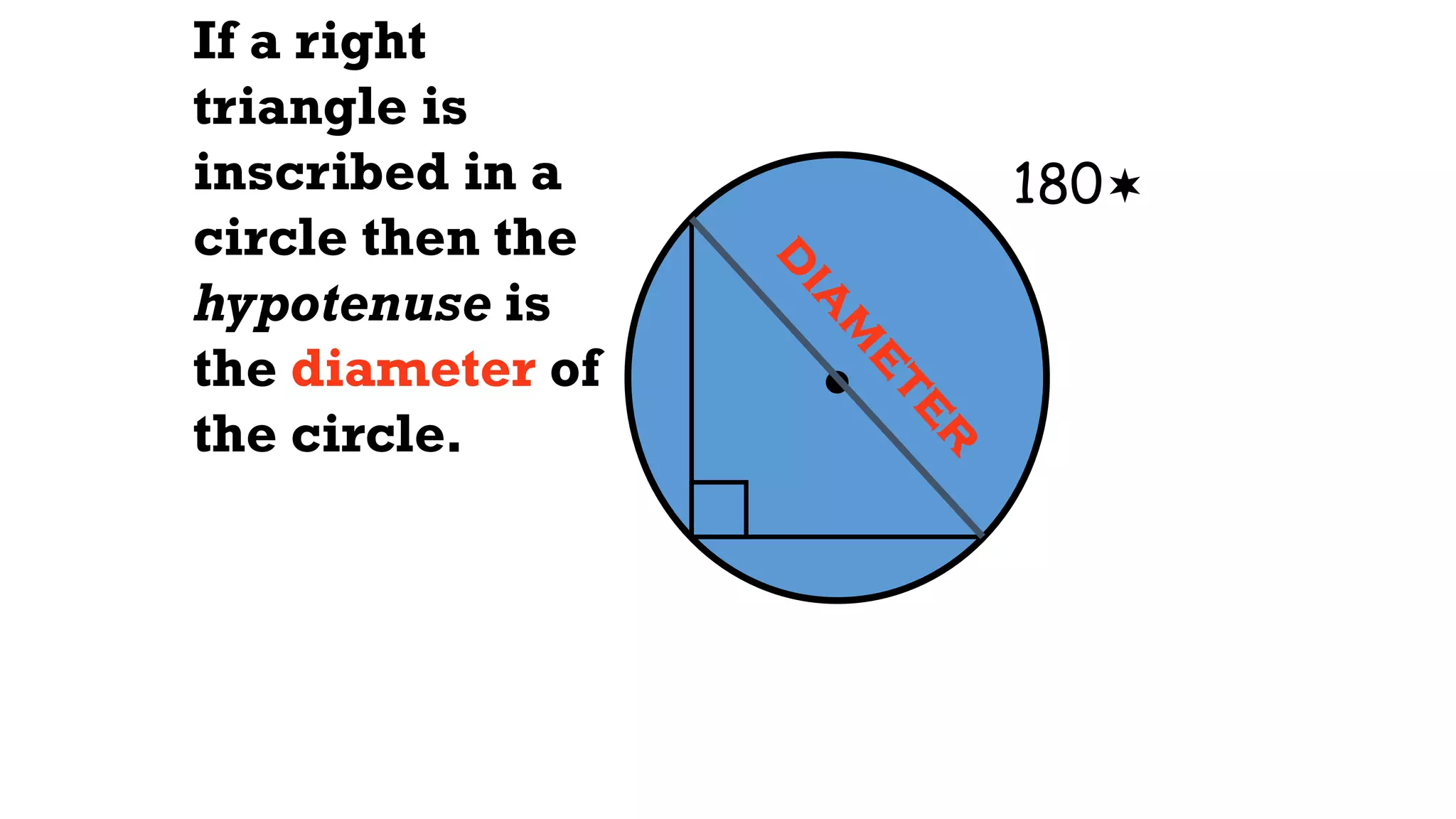
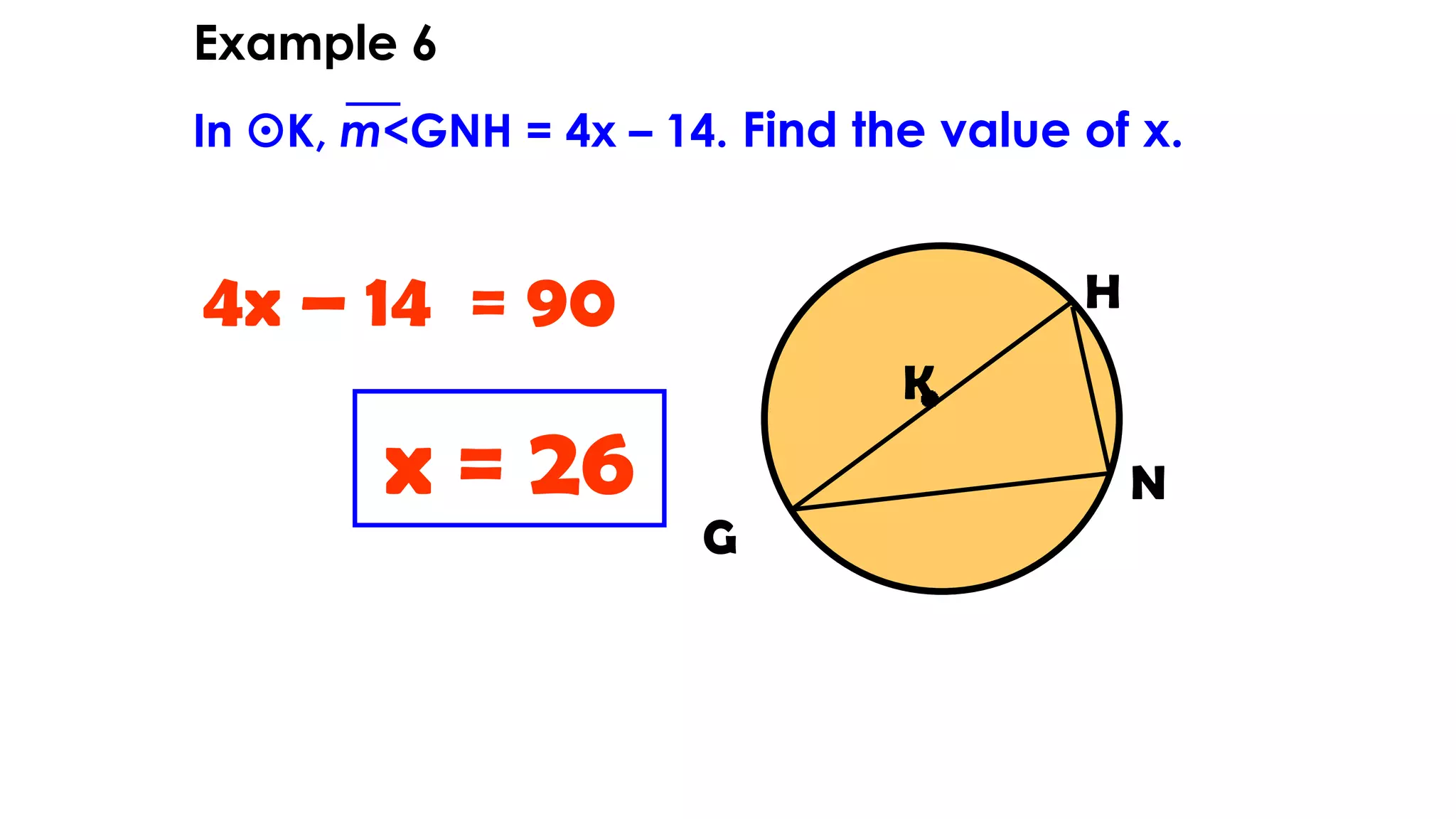
This document discusses circle geometry and contains the following key points:
- It defines important parts of a circle like radii, chords, diameters, and arcs.
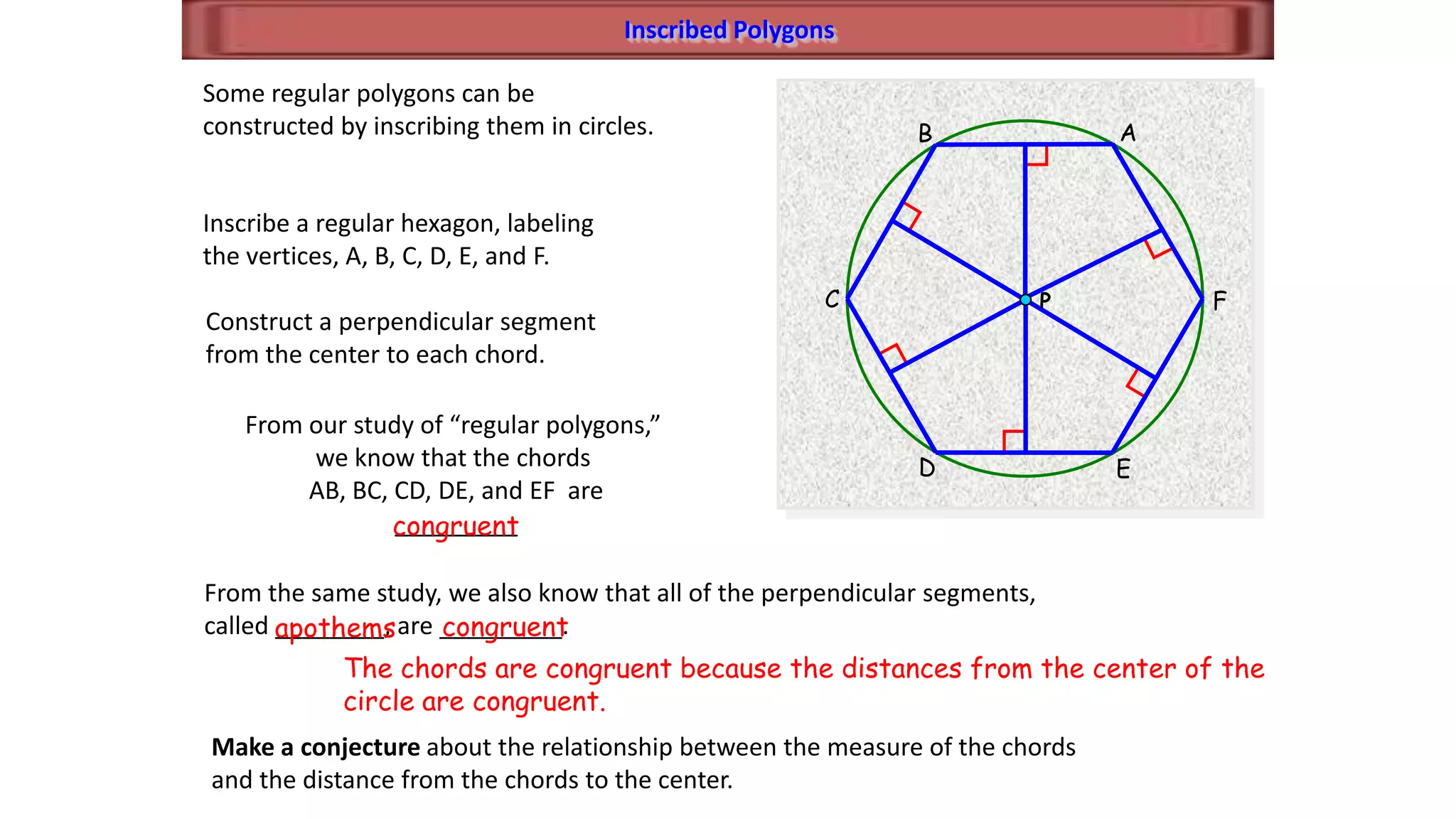
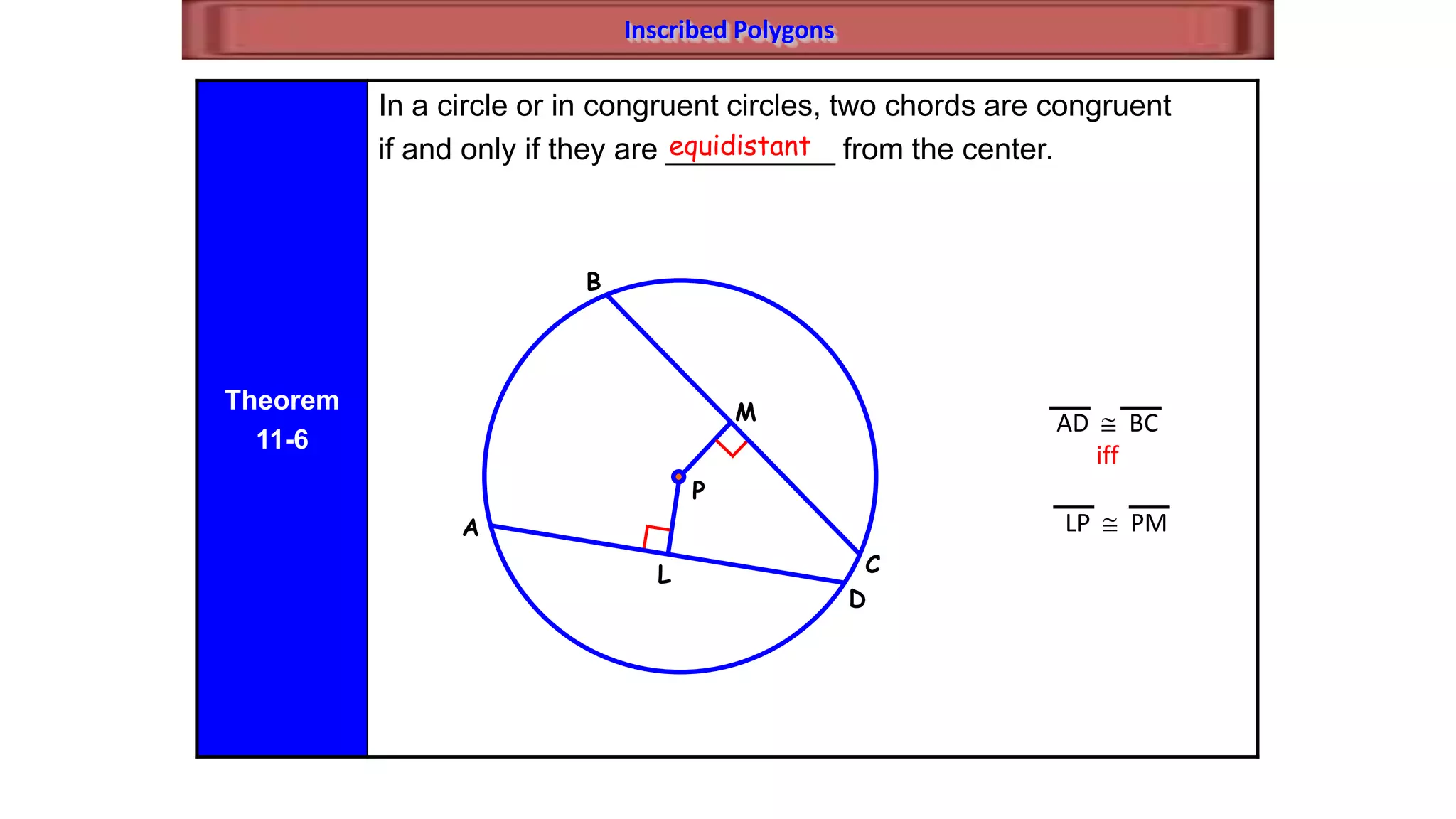
- It establishes theorems relating radii and diameters, congruent arcs and angles, congruent chords and arcs, and the relationships between chords, arcs, and diameters.
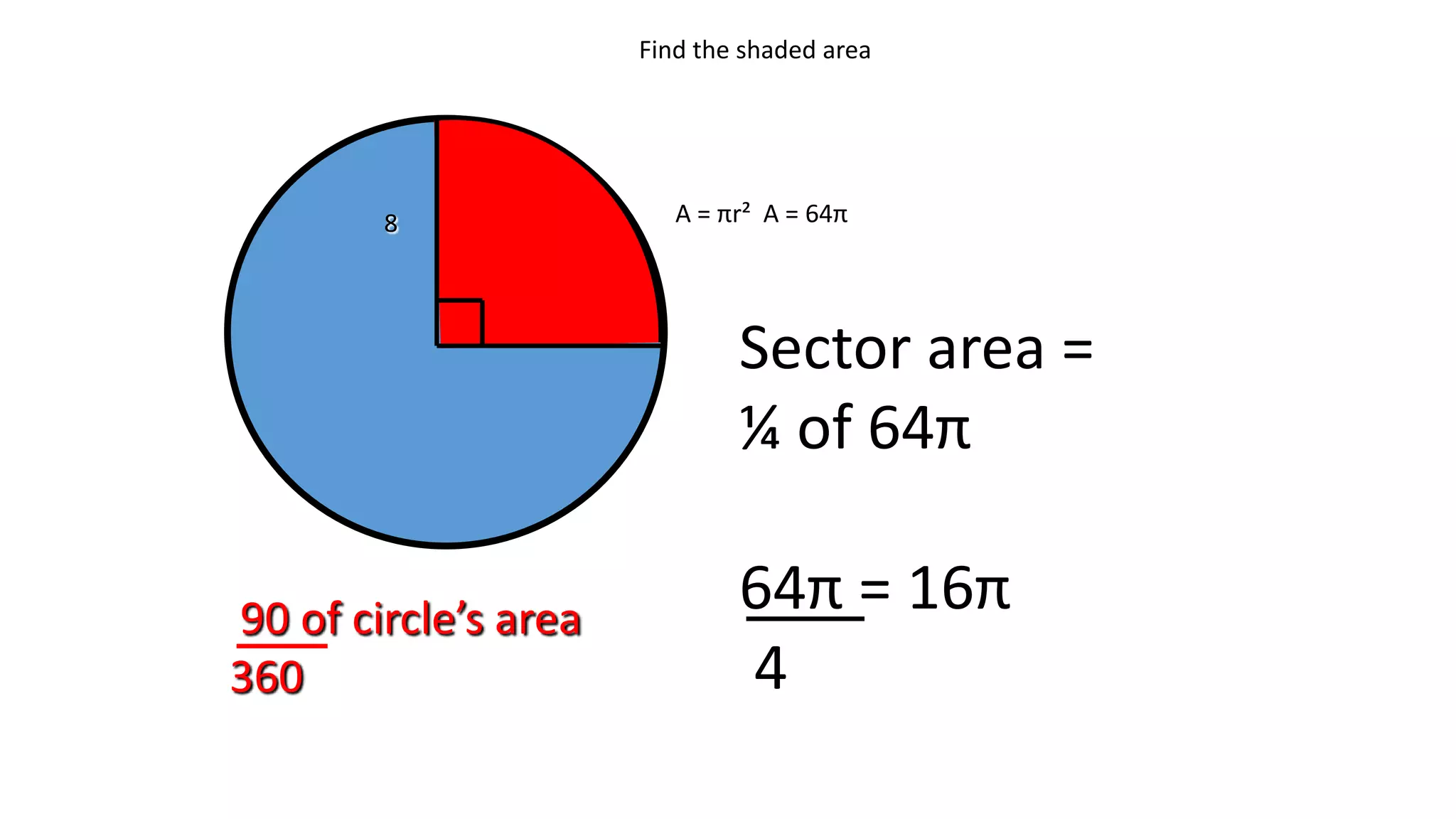
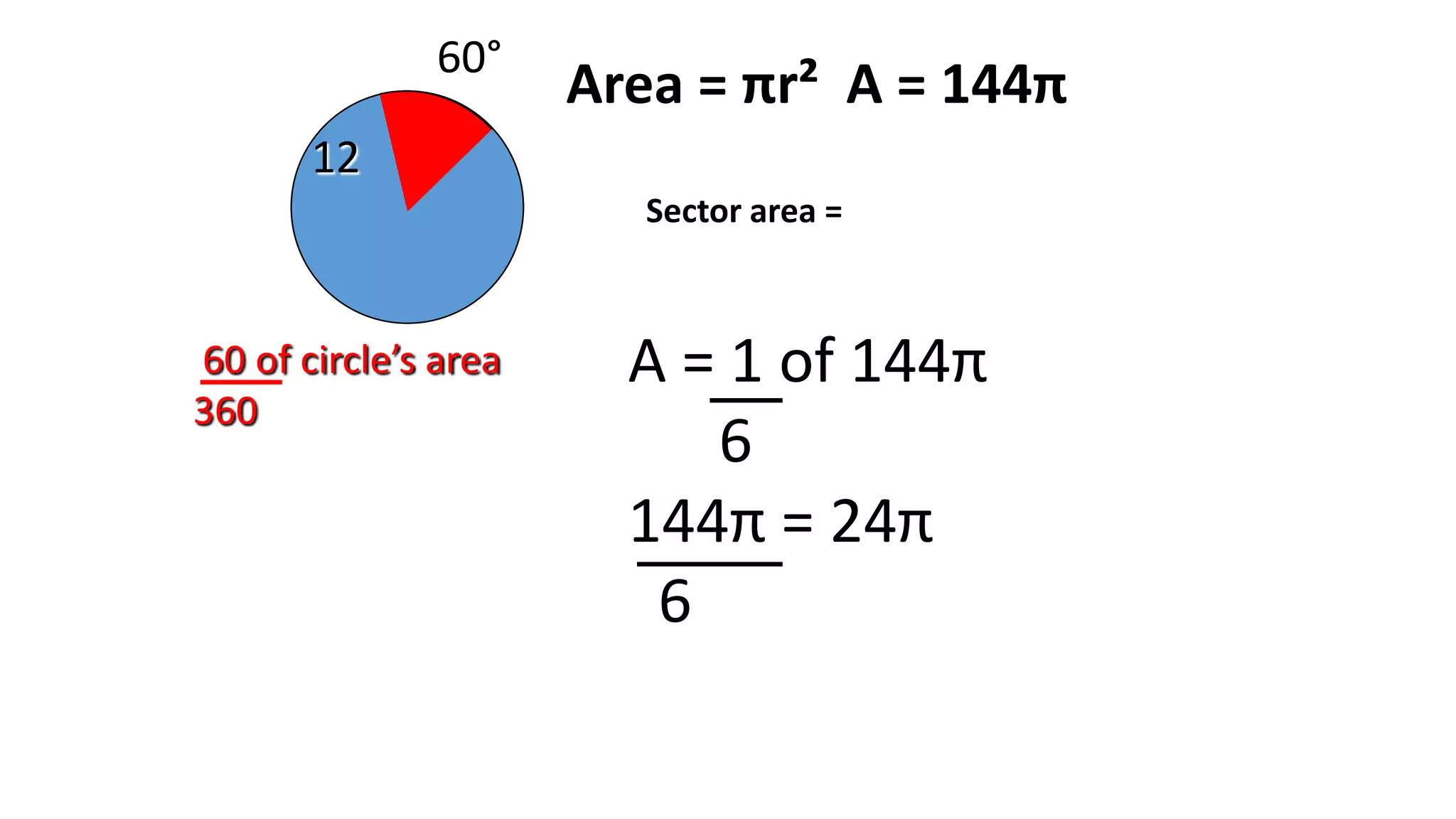
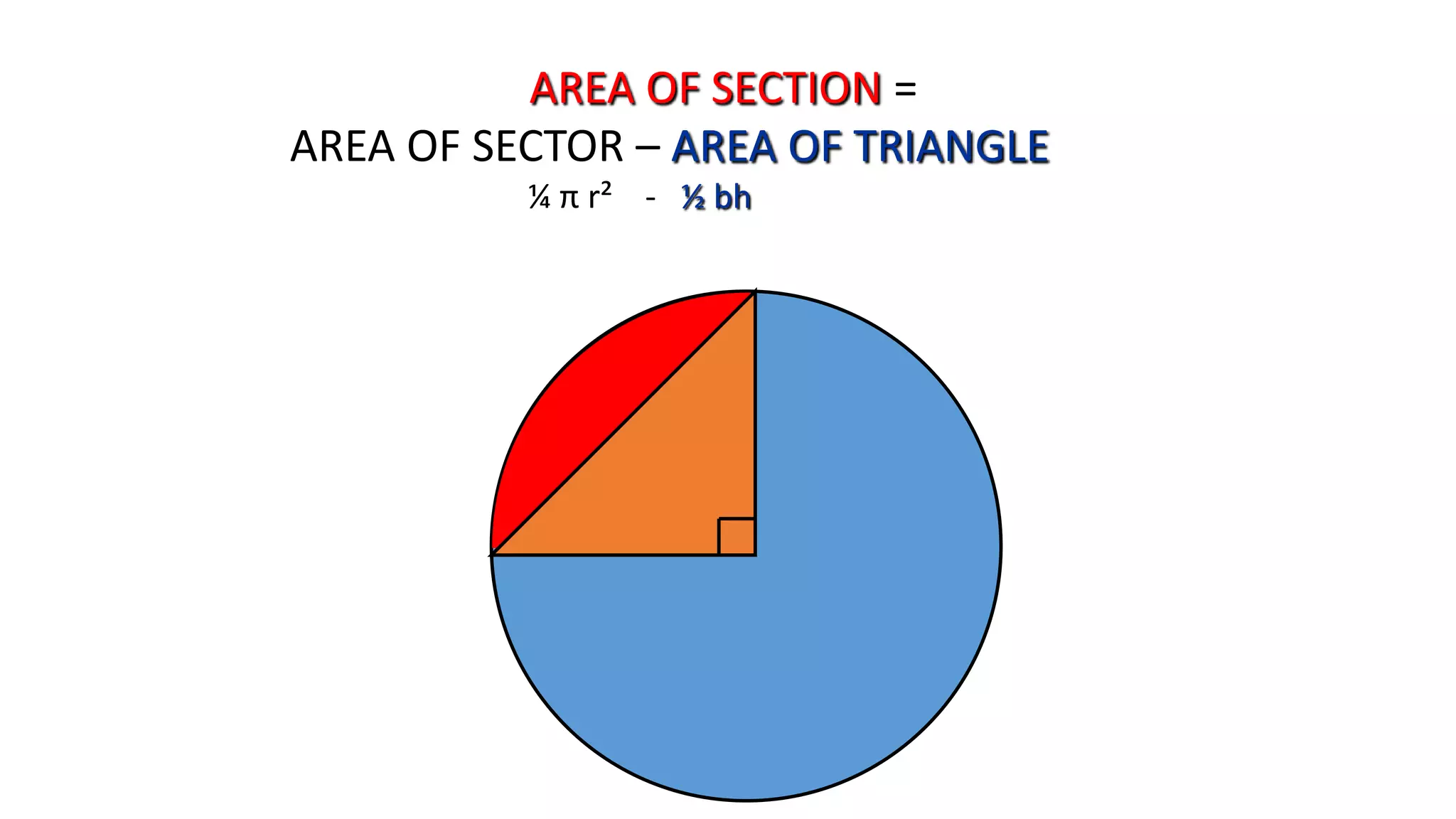
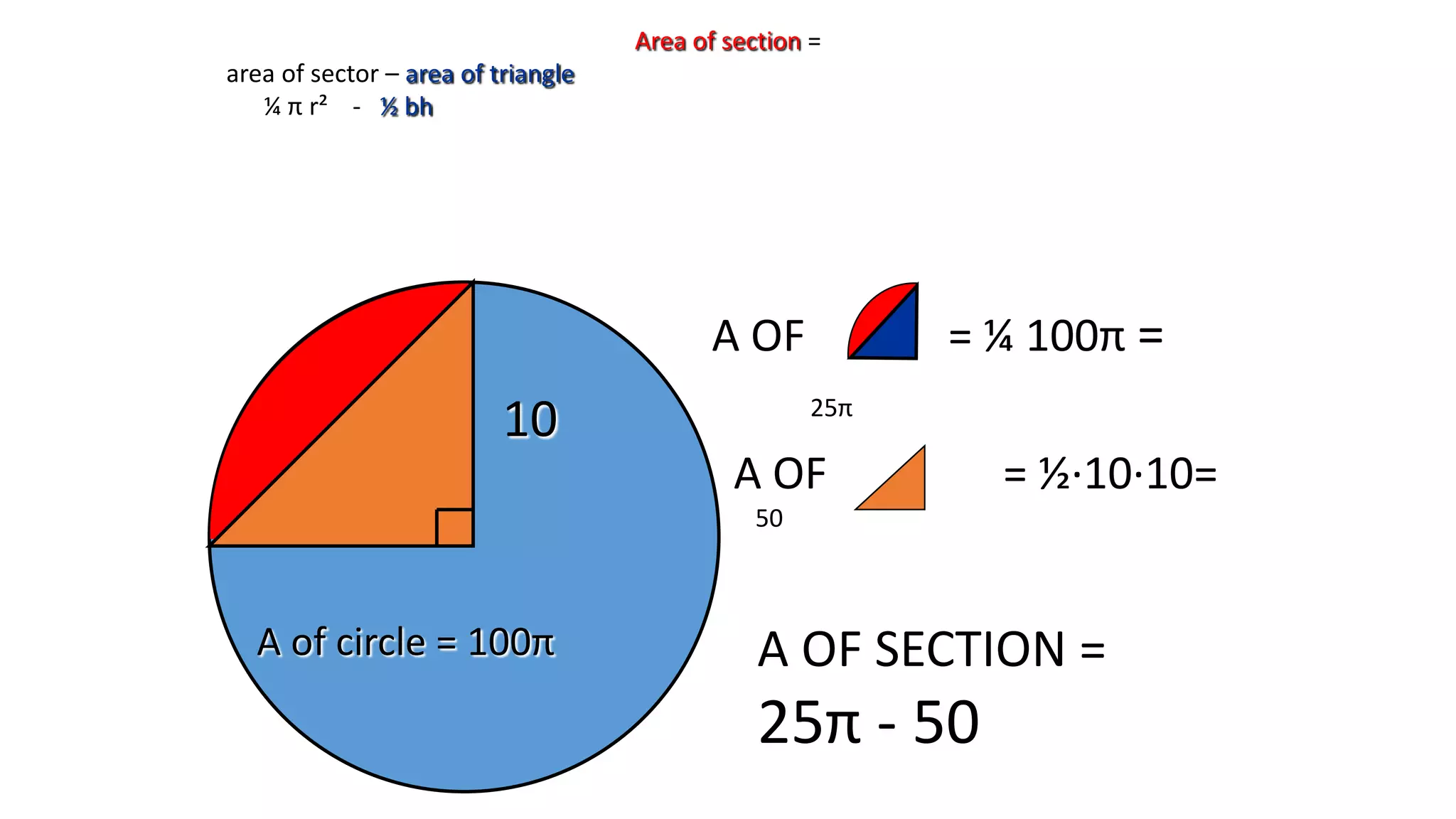
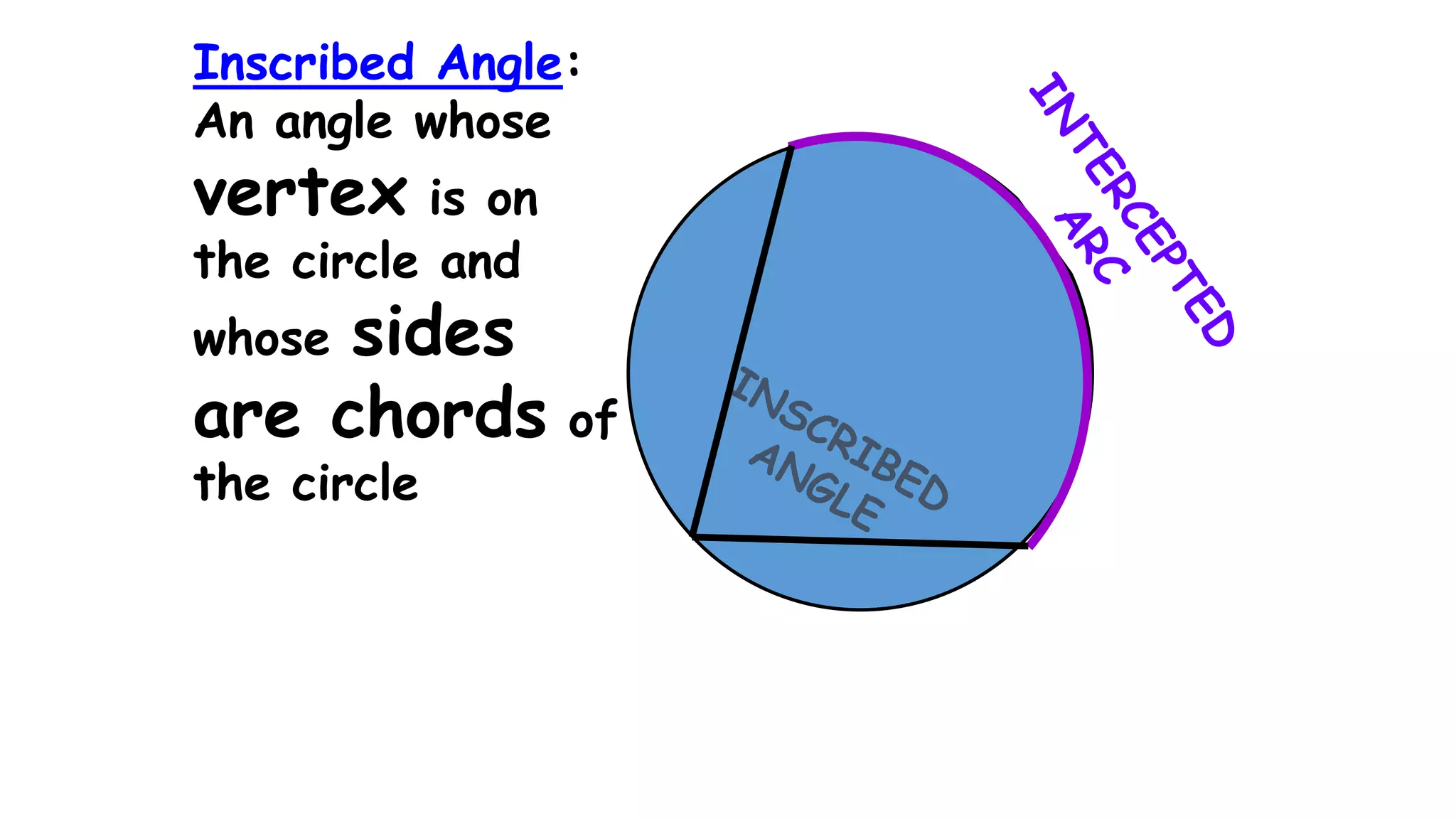
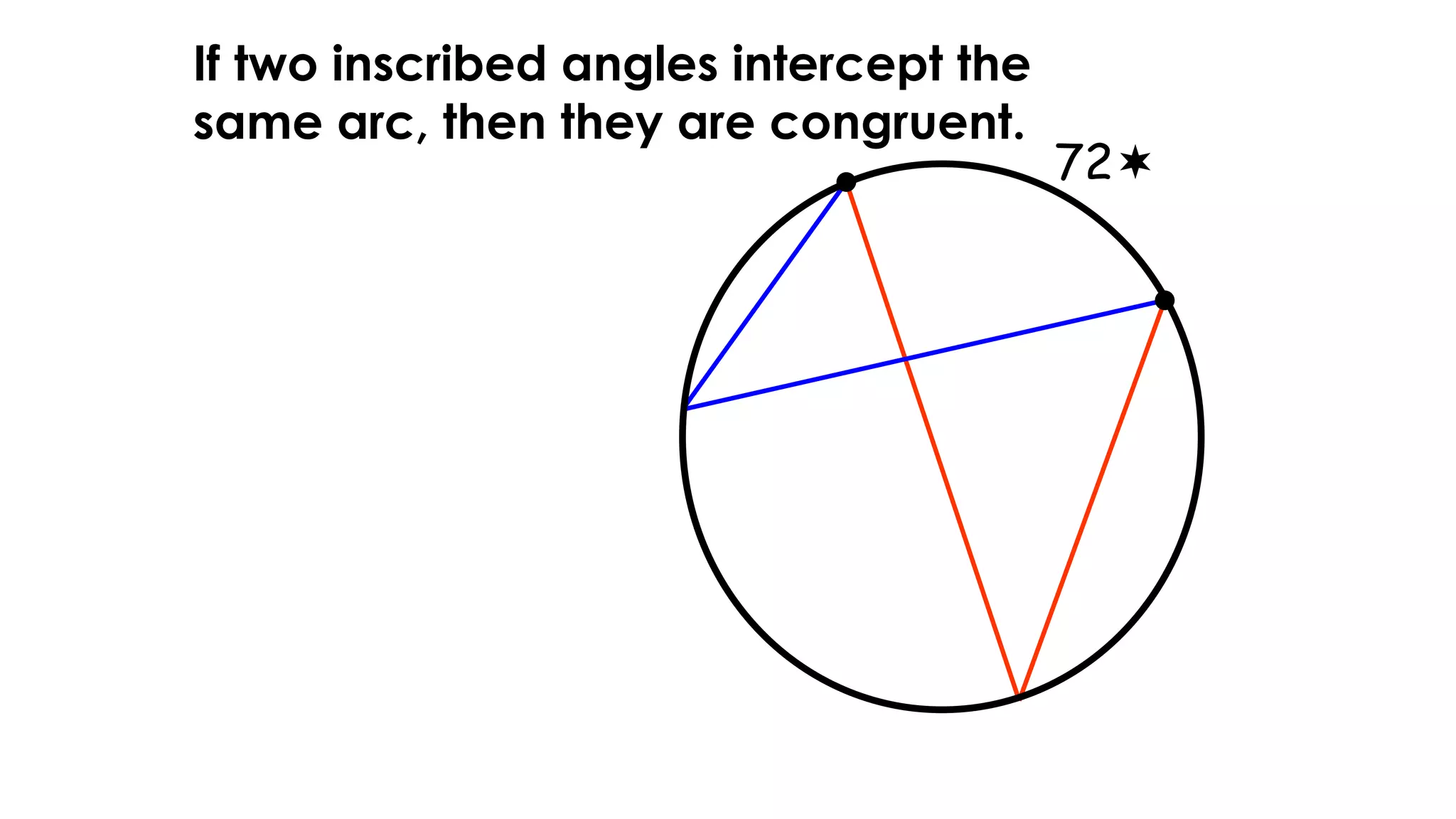
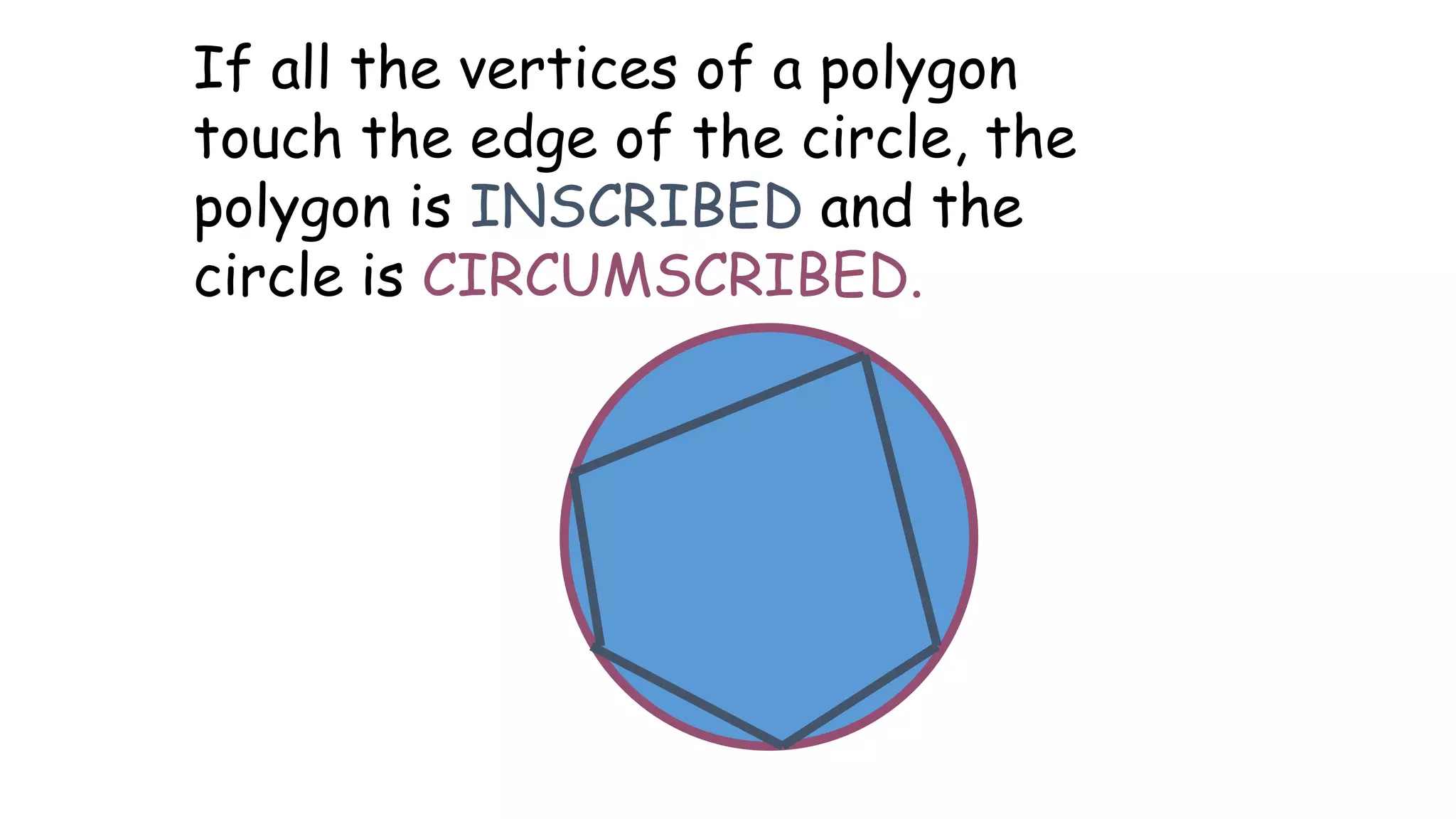
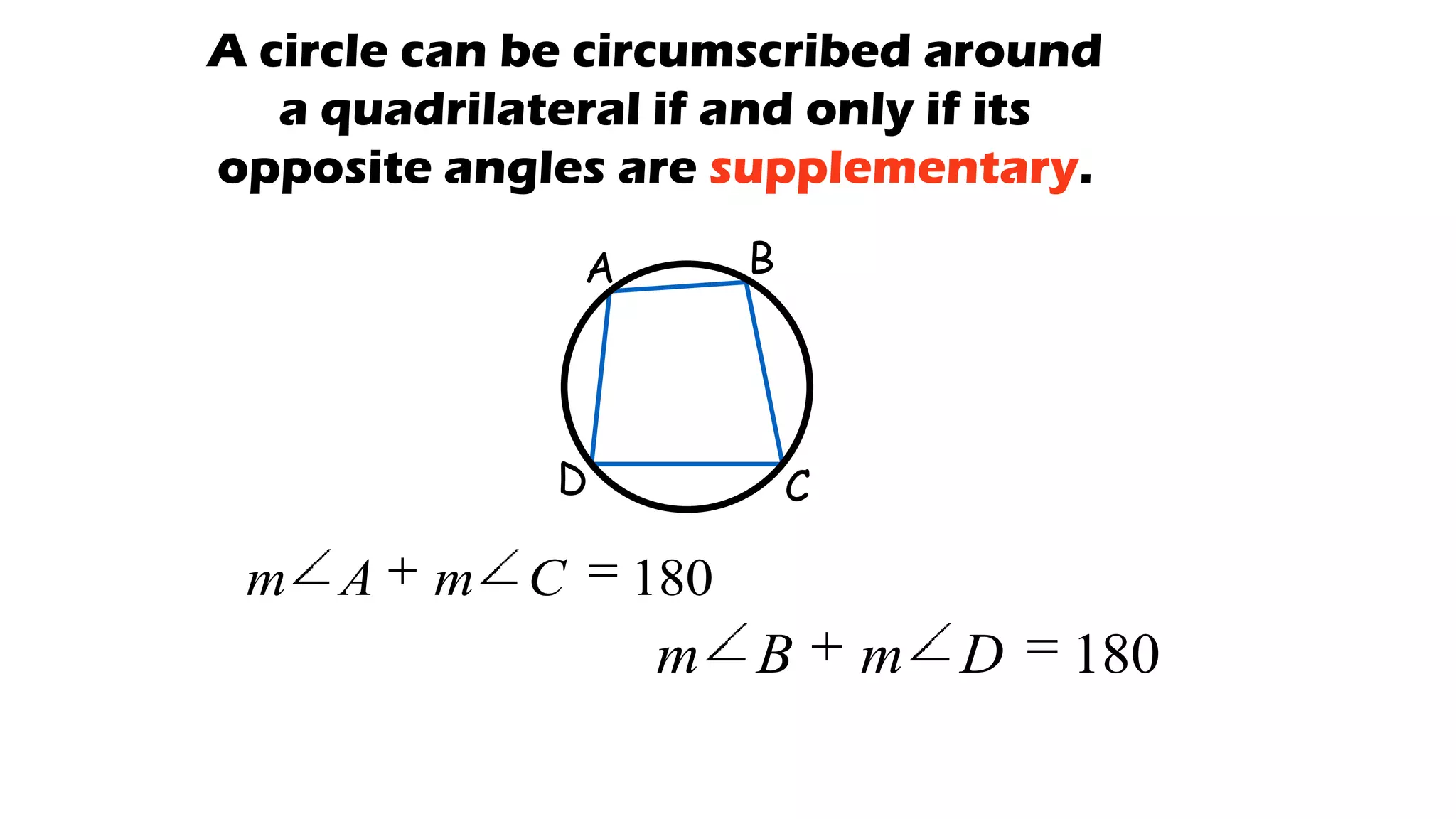
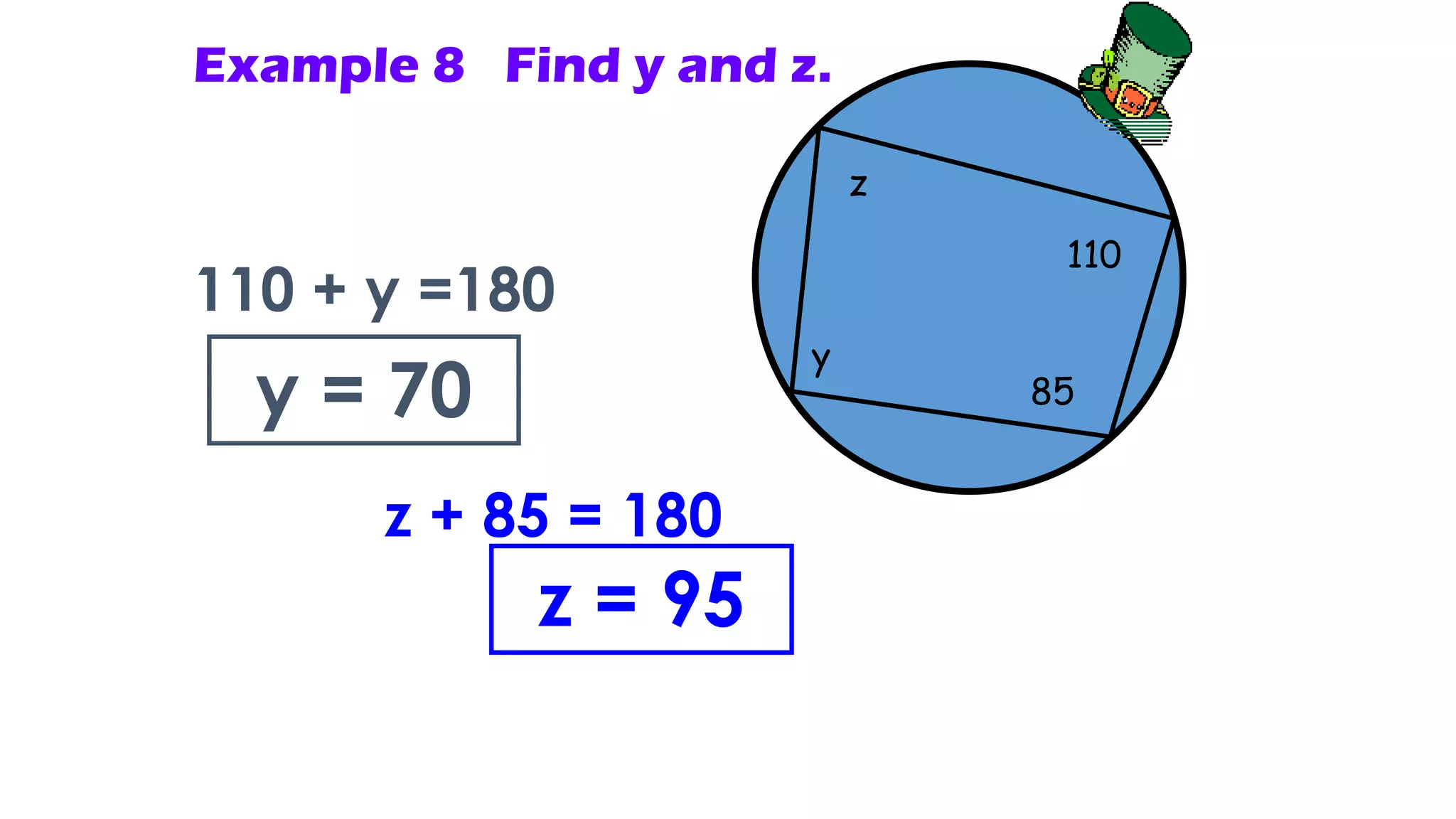
- It describes how to calculate arc measures, circumference, area of circles and sectors, and properties of inscribed angles and polygons.