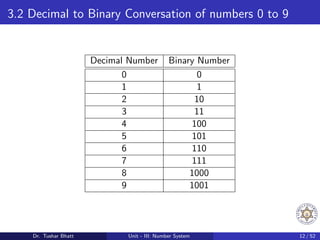
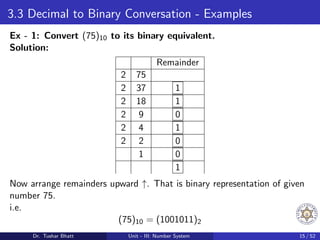
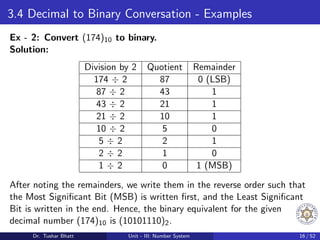
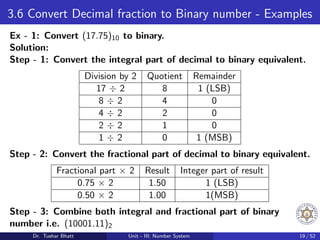
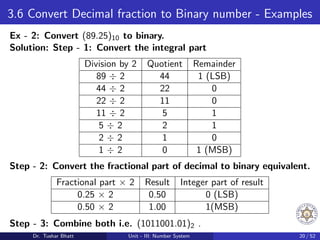
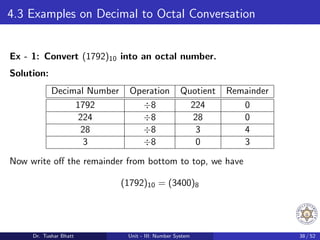
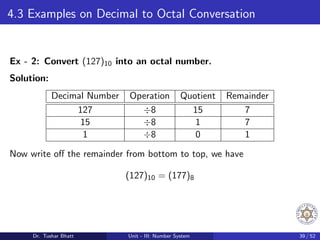
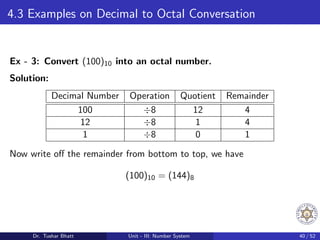
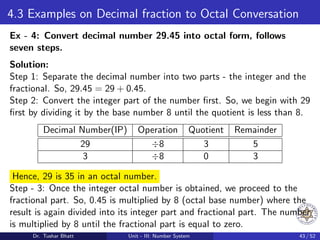
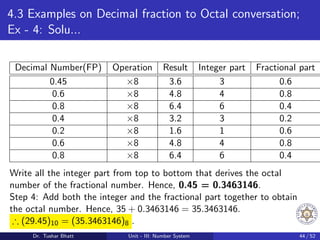
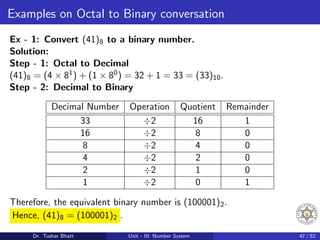
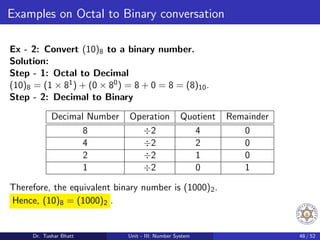
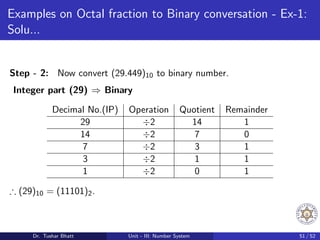
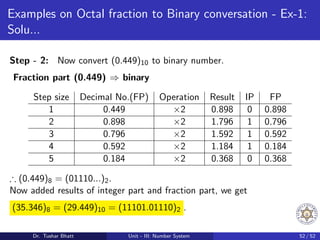
This document discusses number systems, including the decimal, binary, and octal systems. It begins by introducing positional and non-positional number systems. The decimal system uses base 10 with digits 0-9, where the place value of each digit depends on its position. The binary system uses base 2 with digits 0-1. Conversions between decimal, binary, and octal systems are demonstrated through examples such as decimal to binary conversion by repeated division. Fractions are also converted between number systems. Finally, the octal system is introduced, which uses base 8 with digits 0-7.

1. Unit - III: Number System
Dr. Tushar Bhatt
Assistant Professor in Mathematics
Department of Science and Technology
Faculty of Engineering and Technology
Atmiya University
Rajkot - 360005
Dr. Tushar Bhatt Unit - III: Number System 1 / 52

2. Table of Content
1 Introduction
2 Decimal Number System (Base 10)
3 Binary Number System (Base 2)
4 Conversation - I: Decimal to Binary
5 Conversation - II: Decimal fraction to Binary
6 Conversation - III: Binary to Decimal
7 Conversation - IV: Binary fraction to Decimal
8 Octal Number System (Base 8)
9 Conversation - V: Octal to Decimal
10 Conversation - VI: Octal fraction to Decimal
11 Conversation - VII: Decimal to Octal
12 Conversation - VIII: Decimal fraction to Octal
13 Conversation - IX: Octal to Binary
14 Conversation - X: Octal fraction to Binary
Dr. Tushar Bhatt Unit - III: Number System 2 / 52

3. 1. Introduction
A digital computer manipulates discrete elements of data and that these
elements are represented in the binary forms. Operands used for calculations
can be expressed in the binary number system.
Other discrete elements including the decimal digits, are represented in bi-
nary codes. Data processing is carried out by means of binary logic elements
using binary signals. Quantities are stored in binary storage elements.
The purpose of this unit is to introduce the various binary concepts as a
frame of reference for further study in the succeeding units.
Mainly there are two types of number systems as given below:
1 Non-positional Number system.
2 Positional number system.
Dr. Tushar Bhatt Unit - III: Number System 3 / 52

4. 1.1 Non-positional Number system
In this number system
Use symbols such as I for 1, II for 2, III for 3, IIII for 4, IIIII for 5, etc...
Each symbol represents the same value regardless of its position in
the number.
The symbols are simply added to find out the value of a particular
number.
It is difficult to perform arithmetic with such a number system.
Dr. Tushar Bhatt Unit - III: Number System 4 / 52

5. 1.2 Positional number system
In this number system
Use only a few symbols called digits.
These symbols represent different values depending on the position
they occupy in the number.
The value of each digit is determined by:
1 The digit itself.
2 The position of the digit in the number.
3 The base of the number system.
Radix or base = total number of digits in the number system.
The maximum value of a single digit is always equal to one less than
the value of the base.
Dr. Tushar Bhatt Unit - III: Number System 5 / 52

6. 1.3 Categories of positional number systems
There are four categories of positional number system defined as follows:
1 Decimal Number System.
2 Binary Number System.
3 Octal Number System.
4 Hexadecimal Binary Number System.
Dr. Tushar Bhatt Unit - III: Number System 6 / 52

7. 2. Decimal Number System (Base 10)
Decimal number system have ten digits represented by
0,1,2,3,4,5,6,7,8 and 9. So, the base or radix of such system is 10.
In this system the successive position to the left of the decimal point
represent units, tens, hundreds, thousands etc.
For example, if we consider a decimal number 257, then the digit
representations are,
Position Position Position
Hundred Tens Ones
2 5 7
The weight of each digit of a number depends on its relative position within
the number.
Dr. Tushar Bhatt Unit - III: Number System 7 / 52

8. 2.1 Decimal Number System (Base 10) - Example
Ex - 1 : The weight of each digit of the decimal number 6472
6472 = 6000 + 400 + 70 + 2
= (6 × 103
) + (4 × 102
) + (7 × 101
) + (2 × 100
)
∴ The weight of digits from right hand side are
Weight of 1st digit = 2 × 100.
Weight of 2nd digit = 7 × 101.
Weight of 3rd digit = 4 × 102.
Weight of 4th digit = 6 × 103.
The above expressions can be written in general forms as the weight of nth
digit of the number from the right hand side
= nth
digit × 10n−1
Dr. Tushar Bhatt Unit - III: Number System 8 / 52

9. 3. Binary Number System (Base 2)
Only two digits 0 and 1 are used to represent a binary number system. So
the base or radix of binary system is two (2). The digits 0 and 1 are called
bits (Binary Digits). In this number system the value of the digit will be
two times greater than its predecessor. Thus the value of the places are
< ... < −32 < −16 < −8 < −4 < −2 < −1 < ...
The weight of each binary bit depends on its relative position within the
number. It is explained by the following example:
The weight of bits of the binary number 10110 is:
10110 = (1 × 24
) + (0 × 23
) + (1 × 22
) + (1 × 21
) + (0 × 20
)
= 16 + 0 + 4 + 2 + 0
= 22(decimal number)
Dr. Tushar Bhatt Unit - III: Number System 9 / 52

10. 3. Binary Number System (Base 2)
The weight of each bit of a binary no. depends on its relative pointer
within the number and explained from right hand side
∴ The weight of digits from right hand side are
Weight of 1st bit = 0 × 20.
Weight of 2nd bit = 1 × 21.
Weight of 3rd bit = 1 × 22.
Weight of 4th bit = 0 × 23.
Weight of 5th bit = 1 × 24.
The above expressions can be written in general forms as the weight of nth
digit of the number from the right hand side
= nth
bit × 2n−1
Dr. Tushar Bhatt Unit - III: Number System 10 / 52

11. 3.1 How to convert Decimal number to Binary number?
Divide the given decimal number by 2 and note down the remainder.
Now, divide the obtained quotient by 2, and note the remainder again.
Repeat the above steps until you get 0 as the quotient.
Now, write the remainders in such a way that the last remainder is
written first, followed by the rest in the reverse order.
This can also be understood in another way which states that the
Least Significant Bit (LSB) of the binary number is at the top and
the Most Significant Bit (MSB) is at the bottom. This number is the
binary value of the given decimal number.
Dr. Tushar Bhatt Unit - III: Number System 11 / 52

12. 3.2 Decimal to Binary Conversation of numbers 0 to 9
Decimal Number Binary Number
0 0
1 1
2 10
3 11
4 100
5 101
6 110
7 111
8 1000
9 1001
Dr. Tushar Bhatt Unit - III: Number System 12 / 52

13. 3.3 Decimal to Binary Conversation - Example
Dr. Tushar Bhatt Unit - III: Number System 13 / 52

14. Conversation - I
Decimal ⇒ Binary
Dr. Tushar Bhatt Unit - III: Number System 14 / 52

15. 3.3 Decimal to Binary Conversation - Examples
Ex - 1: Convert (75)10 to its binary equivalent.
Solution:
Remainder
2 75
2 37 1
2 18 1
2 9 0
2 4 1
2 2 0
1 0
1
Now arrange remainders upward ↑. That is binary representation of given
number 75.
i.e.
(75)10 = (1001011)2
Dr. Tushar Bhatt Unit - III: Number System 15 / 52

16. 3.4 Decimal to Binary Conversation - Examples
Ex - 2: Convert (174)10 to binary.
Solution:
Division by 2 Quotient Remainder
174 ÷ 2 87 0 (LSB)
87 ÷ 2 43 1
43 ÷ 2 21 1
21 ÷ 2 10 1
10 ÷ 2 5 0
5 ÷ 2 2 1
2 ÷ 2 1 0
1 ÷ 2 0 1 (MSB)
After noting the remainders, we write them in the reverse order such that
the Most Significant Bit (MSB) is written first, and the Least Significant
Bit is written in the end. Hence, the binary equivalent for the given
decimal number (174)10 is (10101110)2.
Dr. Tushar Bhatt Unit - III: Number System 16 / 52

17. Conversation - II
Decimal fraction ⇒ Binary
Dr. Tushar Bhatt Unit - III: Number System 17 / 52

18. 3.5 Convert Decimal fraction to Binary number - Steps
For this conversations, we will consider following three steps:
1 Convert the integral part of decimal to binary equivalent.
Divide the decimal number by 2 and store remainders in array.
Divide the quotient by 2.
Repeat step 2 until we get the quotient equal to zero.
Equivalent binary number would be reverse of all remainders of step 1.
2 Convert the fractional part of decimal to binary equivalent
Multiply the fractional decimal number by 2
Integral part of resultant decimal number will be first digit of fraction
binary number.
Repeat step 1 using only fractional part of decimal number and then
step 2.
If any fraction will have more and more fractions after multiply by 2
then fix the step size according to given instruction.
In the fraction part must arrange the integer part in the downward
direction ↓.
3 Combine both integral and fractional part of binary number.
Dr. Tushar Bhatt Unit - III: Number System 18 / 52

19. 3.6 Convert Decimal fraction to Binary number - Examples
Ex - 1: Convert (17.75)10 to binary.
Solution:
Step - 1: Convert the integral part of decimal to binary equivalent.
Division by 2 Quotient Remainder
17 ÷ 2 8 1 (LSB)
8 ÷ 2 4 0
4 ÷ 2 2 0
2 ÷ 2 1 0
1 ÷ 2 0 1 (MSB)
Step - 2: Convert the fractional part of decimal to binary equivalent.
Fractional part × 2 Result Integer part of result
0.75 × 2 1.50 1 (LSB)
0.50 × 2 1.00 1(MSB)
Step - 3: Combine both integral and fractional part of binary
number i.e. (10001.11)2
Dr. Tushar Bhatt Unit - III: Number System 19 / 52

20. 3.6 Convert Decimal fraction to Binary number - Examples
Ex - 2: Convert (89.25)10 to binary.
Solution: Step - 1: Convert the integral part
Division by 2 Quotient Remainder
89 ÷ 2 44 1 (LSB)
44 ÷ 2 22 0
22 ÷ 2 11 0
11 ÷ 2 5 1
5 ÷ 2 2 1
2 ÷ 2 1 0
1 ÷ 2 0 1 (MSB)
Step - 2: Convert the fractional part of decimal to binary equivalent.
Fractional part × 2 Result Integer part of result
0.25 × 2 0.50 0 (LSB)
0.50 × 2 1.00 1(MSB)
Step - 3: Combine both i.e. (1011001.01)2 .
Dr. Tushar Bhatt Unit - III: Number System 20 / 52

21. Conversation - III
Binary ⇒ Decimal
Dr. Tushar Bhatt Unit - III: Number System 21 / 52

22. 3.7 How to convert Binary number to Decimal number?
We know that the binary to decimal number system conversion is the
process of changing from a binary (base 2) to a decimal number
system (base 10 number system).
To convert a binary number system to a decimal number system,
follow the procedures below.
Step - 1: Multiply each digit of the specified binary number by the
exponents of the base starting with the right most digit (i.e.,
20, 21, 22, and so on).
Step - 2: As we move right to left, the exponents should increase by
one, such that the exponents begin with 0.
Step - 3: Simplify and find the sum of each of the product values
obtained in the previous steps.
Dr. Tushar Bhatt Unit - III: Number System 22 / 52

23. 3.8 Binary to Decimal conversation examples
Ex - 1: Convert (11110)2 into a decimal number system.
Solution:
11110 = (1 × 24
) + (1 × 23
) + (1 × 22
) + (1 × 21
) + (0 × 20
)
= (16) + (8) + (4) + (2) + (1)
= 30
∴ (11110)2 = (30)10.
Dr. Tushar Bhatt Unit - III: Number System 23 / 52

24. 3.8 Binary to Decimal conversation examples
Ex - 2: Convert (0110)2 into a decimal number system.
Solution:
0110 = (0 × 23
) + (1 × 22
) + (1 × 21
) + (0 × 20
)
= (0) + (4) + (2) + (0)
= 6
∴ (0110)2 = (6)10.
Dr. Tushar Bhatt Unit - III: Number System 24 / 52

25. 3.8 Binary to Decimal conversation examples
Ex - 3: Convert (1110110)2 into a decimal number system.
Solution:
1110110 = (1 × 26
) + (1 × 25
) + (1 × 24
) + (0 × 23
)
+ (1 × 22
) + (1 × 21
) + (0 × 20
)
= (64) + (32) + (16) + (0) + (4) + (2) + (0)
= 118
∴ (1110110)2 = (118)10.
Dr. Tushar Bhatt Unit - III: Number System 25 / 52

26. 3.8 Binary to Decimal conversation examples
Ex - 4: The binary number (1111)2 is equal to (x)10.Then find the
value of x.
Solution:
1111 = (1 × 23
) + (1 × 22
) + (1 × 21
) + (1 × 20
)
= (8) + (4) + (2) + (1)
= 15
∴ (1111)2 = (15)10.
∴ x = 15.
Dr. Tushar Bhatt Unit - III: Number System 26 / 52

27. Conversation - IV
Binary fraction ⇒ Decimal
Dr. Tushar Bhatt Unit - III: Number System 27 / 52

28. 3.9 Fraction Binary number to Decimal number
conversation
Ex - 5: Convert (1110.1010)2 into a decimal number system.
Solution:
Here first we have to separate the integral and fraction part
Integral Part: 1110
1110 = (1 × 23) + (1 × 22) + (1 × 21) + (0 × 20) = 14
Fractional Part: .1010
.1010 = (1 × 2−1) + (0 × 2−2) + (1 × 2−3) + (0 × 2−4) = 1
2 + 0 + 1
8 + 0 =
0.5 + 0.125 = 0.625
Now
(1110.1010)2 = Integral part + Fractional part = 14 + 0.625 = 14.625
.
∴
(1110.1010)2 = (14.625)10
Dr. Tushar Bhatt Unit - III: Number System 28 / 52

29. 4. Octal Number System (Base 8)
A commonly used positional number system is the Octal Number
System. This system has eight (8) digit representations as
0,1,2,3,4,5,6 and 7. The base or radix of this system is 8.
The maximum value of a single digit is 7 (one less than the value of
the base.
Each position of a digit represents a specific power of the base (8).
Since there are only 8 digits, 3 bits (23 = 8) are sufficient to represent
any octal number in binary.
Dr. Tushar Bhatt Unit - III: Number System 29 / 52

30. Conversation - V
Octal ⇒ Decimal
Dr. Tushar Bhatt Unit - III: Number System 30 / 52

31. 4.1 Steps to Convert Octal to Decimal
Step - 1: Since an octal number only uses digits from 0 to 7, we first
arrange the octal number with the power of 8.
Step - 2: We evaluate all the power of 8 values such as 80 is 1, 81 is
8, etc., and write down the value of each octal number.
Step - 3: Once the value is obtained, we multiply each number.
Step - 4: Final step is to add the product of all the numbers to obtain
the decimal number.
Dr. Tushar Bhatt Unit - III: Number System 31 / 52

32. 4.2 Examples on Octal to Decimal Conversation
Ex - 1: Convert (140)8 to decimal number.
Solution:
Dr. Tushar Bhatt Unit - III: Number System 32 / 52

33. 4.2 Examples on Octal to Decimal Conversation
Ex - 2: Convert (2057)8 to decimal number.
Solution:
(2057)8 = (2 × 83
) + (0 × 82
) + (5 × 81
) + (7 × 80
)
= 1024 + 0 + 40 + 7
= 1071
∴ (2057)8 = (1071)10
Dr. Tushar Bhatt Unit - III: Number System 33 / 52

34. Conversation - VI
Octal fraction ⇒ Decimal
Dr. Tushar Bhatt Unit - III: Number System 34 / 52

35. 4.2 Examples on Octal to Decimal Conversation
Ex - 3: Convert (246.28)8 to decimal number.
Solution:
Dr. Tushar Bhatt Unit - III: Number System 35 / 52

36. Conversation - VII
Decimal ⇒ Octal
Dr. Tushar Bhatt Unit - III: Number System 36 / 52

37. 4.3 Decimal to Octal conversation
Dr. Tushar Bhatt Unit - III: Number System 37 / 52

38. 4.3 Examples on Decimal to Octal Conversation
Ex - 1: Convert (1792)10 into an octal number.
Solution:
Decimal Number Operation Quotient Remainder
1792 ÷8 224 0
224 ÷8 28 0
28 ÷8 3 4
3 ÷8 0 3
Now write off the remainder from bottom to top, we have
(1792)10 = (3400)8
Dr. Tushar Bhatt Unit - III: Number System 38 / 52

39. 4.3 Examples on Decimal to Octal Conversation
Ex - 2: Convert (127)10 into an octal number.
Solution:
Decimal Number Operation Quotient Remainder
127 ÷8 15 7
15 ÷8 1 7
1 ÷8 0 1
Now write off the remainder from bottom to top, we have
(127)10 = (177)8
Dr. Tushar Bhatt Unit - III: Number System 39 / 52

40. 4.3 Examples on Decimal to Octal Conversation
Ex - 3: Convert (100)10 into an octal number.
Solution:
Decimal Number Operation Quotient Remainder
100 ÷8 12 4
12 ÷8 1 4
1 ÷8 0 1
Now write off the remainder from bottom to top, we have
(100)10 = (144)8
Dr. Tushar Bhatt Unit - III: Number System 40 / 52

41. Conversation - VIII
Decimal fraction ⇒ Octal
Dr. Tushar Bhatt Unit - III: Number System 41 / 52

42. Steps to Convert Decimal fraction to Octal
1 First, we calculate the integer part of the decimal point by dividing
the octal base number i.e. 8 until the quotient is less than 8.
2 The second part is calculated on the fraction part of the decimal
number where the number is multiplied with the base number 8 until
the fractional part is equal to zero.
3 Here, once multiplied we keep the integer part separate and the
fractional part separate.
4 The final octal number is calculated by adding both the integer and
the fractional number.
Dr. Tushar Bhatt Unit - III: Number System 42 / 52

43. 4.3 Examples on Decimal fraction to Octal Conversation
Ex - 4: Convert decimal number 29.45 into octal form, follows
seven steps.
Solution:
Step 1: Separate the decimal number into two parts - the integer and the
fractional. So, 29.45 = 29 + 0.45.
Step 2: Convert the integer part of the number first. So, we begin with 29
first by dividing it by the base number 8 until the quotient is less than 8.
Decimal Number(IP) Operation Quotient Remainder
29 ÷8 3 5
3 ÷8 0 3
Hence, 29 is 35 in an octal number.
Step - 3: Once the integer octal number is obtained, we proceed to the
fractional part. So, 0.45 is multiplied by 8 (octal base number) where the
result is again divided into its integer part and fractional part. The number
is multiplied by 8 until the fractional part is equal to zero.
Dr. Tushar Bhatt Unit - III: Number System 43 / 52

44. 4.3 Examples on Decimal fraction to Octal conversation;
Ex - 4: Solu...
Decimal Number(FP) Operation Result Integer part Fractional part
0.45 ×8 3.6 3 0.6
0.6 ×8 4.8 4 0.8
0.8 ×8 6.4 6 0.4
0.4 ×8 3.2 3 0.2
0.2 ×8 1.6 1 0.6
0.6 ×8 4.8 4 0.8
0.8 ×8 6.4 6 0.4
Write all the integer part from top to bottom that derives the octal
number of the fractional number. Hence, 0.45 = 0.3463146.
Step 4: Add both the integer and the fractional part together to obtain
the octal number. Hence, 35 + 0.3463146 = 35.3463146.
∴ (29.45)10 = (35.3463146)8 .
Dr. Tushar Bhatt Unit - III: Number System 44 / 52

45. Conversation - IX
Octal ⇒ Binary
Dr. Tushar Bhatt Unit - III: Number System 45 / 52

46. Steps for Convert Octal to Binary
Octal ⇒ Decimal ⇒ Binary
Dr. Tushar Bhatt Unit - III: Number System 46 / 52

47. Examples on Octal to Binary conversation
Ex - 1: Convert (41)8 to a binary number.
Solution:
Step - 1: Octal to Decimal
(41)8 = (4 × 81) + (1 × 80) = 32 + 1 = 33 = (33)10.
Step - 2: Decimal to Binary
Decimal Number Operation Quotient Remainder
33 ÷2 16 1
16 ÷2 8 0
8 ÷2 4 0
4 ÷2 2 0
2 ÷2 1 0
1 ÷2 0 1
Therefore, the equivalent binary number is (100001)2.
Hence, (41)8 = (100001)2 .
Dr. Tushar Bhatt Unit - III: Number System 47 / 52

48. Examples on Octal to Binary conversation
Ex - 2: Convert (10)8 to a binary number.
Solution:
Step - 1: Octal to Decimal
(10)8 = (1 × 81) + (0 × 80) = 8 + 0 = 8 = (8)10.
Step - 2: Decimal to Binary
Decimal Number Operation Quotient Remainder
8 ÷2 4 0
4 ÷2 2 0
2 ÷2 1 0
1 ÷2 0 1
Therefore, the equivalent binary number is (1000)2.
Hence, (10)8 = (1000)2 .
Dr. Tushar Bhatt Unit - III: Number System 48 / 52

49. Conversation - IX
Octal fraction ⇒ Binary
Dr. Tushar Bhatt Unit - III: Number System 49 / 52

50. Examples on Octal fraction to Binary conversation
Ex - 1: Convert (35.346)8 into binary number, follows five steps
Solution:
Step - 1: Here first we convert (35.346)8in decimal numbers.
(36.346)8 = (3 × 81
) + (5 × 80
) + (3 × 8−1
) + (4 × 8−2
) + (6 × 8−3
)
= 24 + 5 + 0.375 + 0.062 + 0.012
= 29.449
= (29.449)10
Dr. Tushar Bhatt Unit - III: Number System 50 / 52

51. Examples on Octal fraction to Binary conversation - Ex-1:
Solu...
Step - 2: Now convert (29.449)10 to binary number.
Integer part (29) ⇒ Binary
Decimal No.(IP) Operation Quotient Remainder
29 ÷2 14 1
14 ÷2 7 0
7 ÷2 3 1
3 ÷2 1 1
1 ÷2 0 1
∴ (29)10 = (11101)2.
Dr. Tushar Bhatt Unit - III: Number System 51 / 52

52. Examples on Octal fraction to Binary conversation - Ex-1:
Solu...
Step - 2: Now convert (0.449)10 to binary number.
Fraction part (0.449) ⇒ binary
Step size Decimal No.(FP) Operation Result IP FP
1 0.449 ×2 0.898 0 0.898
2 0.898 ×2 1.796 1 0.796
3 0.796 ×2 1.592 1 0.592
4 0.592 ×2 1.184 1 0.184
5 0.184 ×2 0.368 0 0.368
∴ (0.449)8 = (01110...)2.
Now added results of integer part and fraction part, we get
(35.346)8 = (29.449)10 = (11101.01110)2 .
Dr. Tushar Bhatt Unit - III: Number System 52 / 52