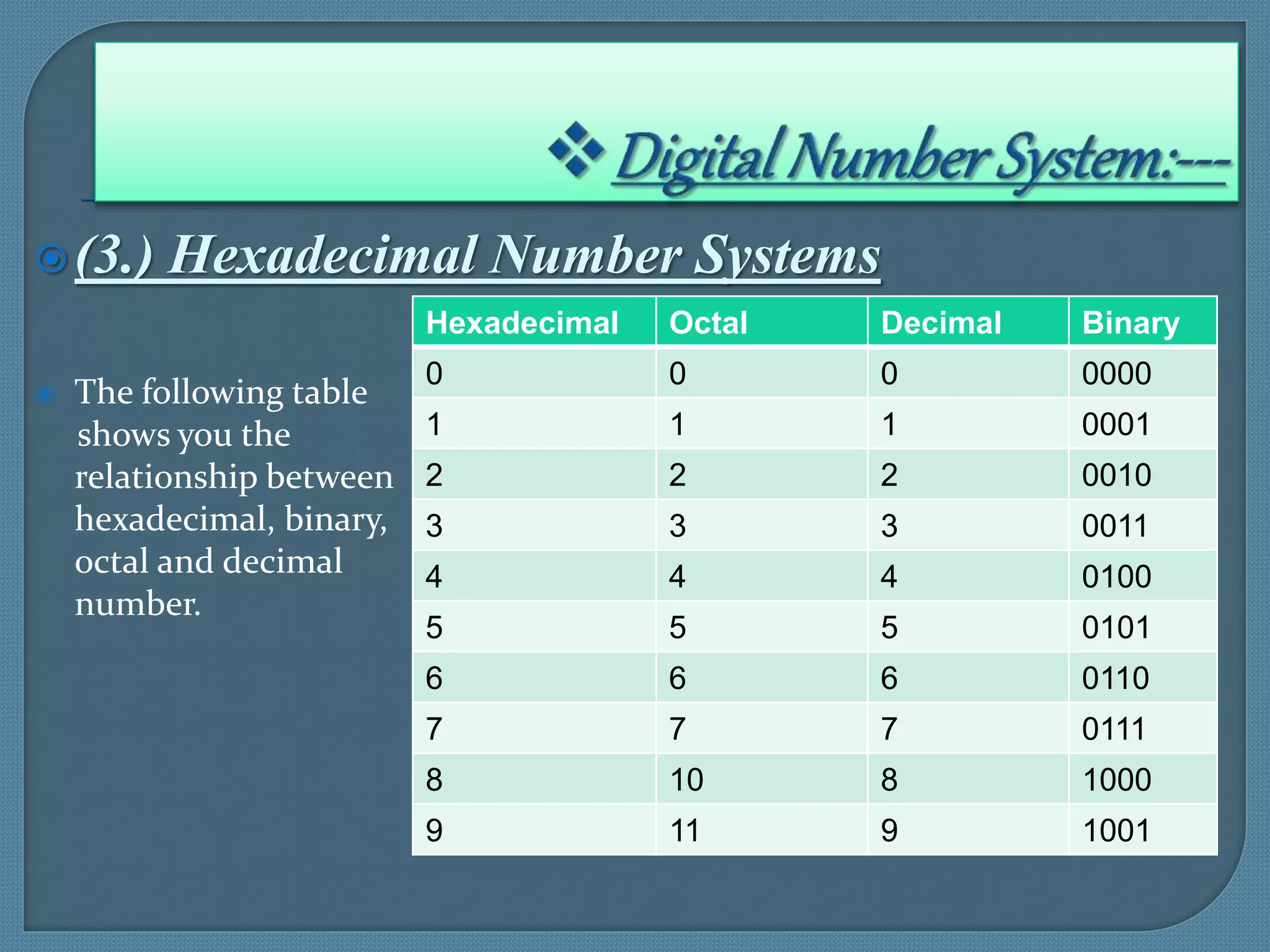
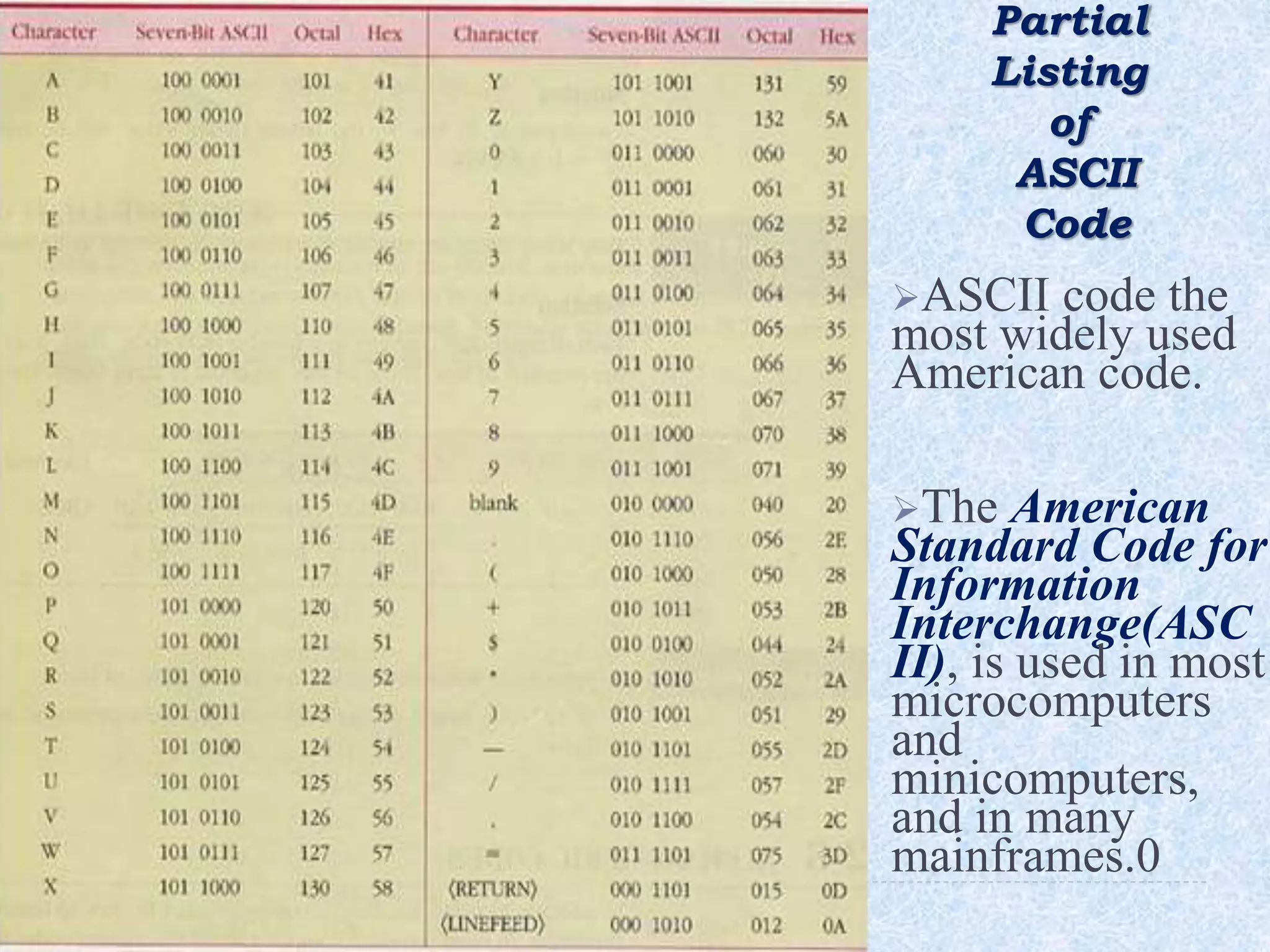
This document discusses different number systems used in digital computers and their conversions. It begins with an introduction to digital number systems and then describes the decimal, binary, octal and hexadecimal number systems. It explains how to represent integers and real numbers in binary. The document also covers number conversions between these systems using different methods like repeated division. Finally, it discusses various ways of representing integers in binary like sign-magnitude, one's complement and two's complement representations.