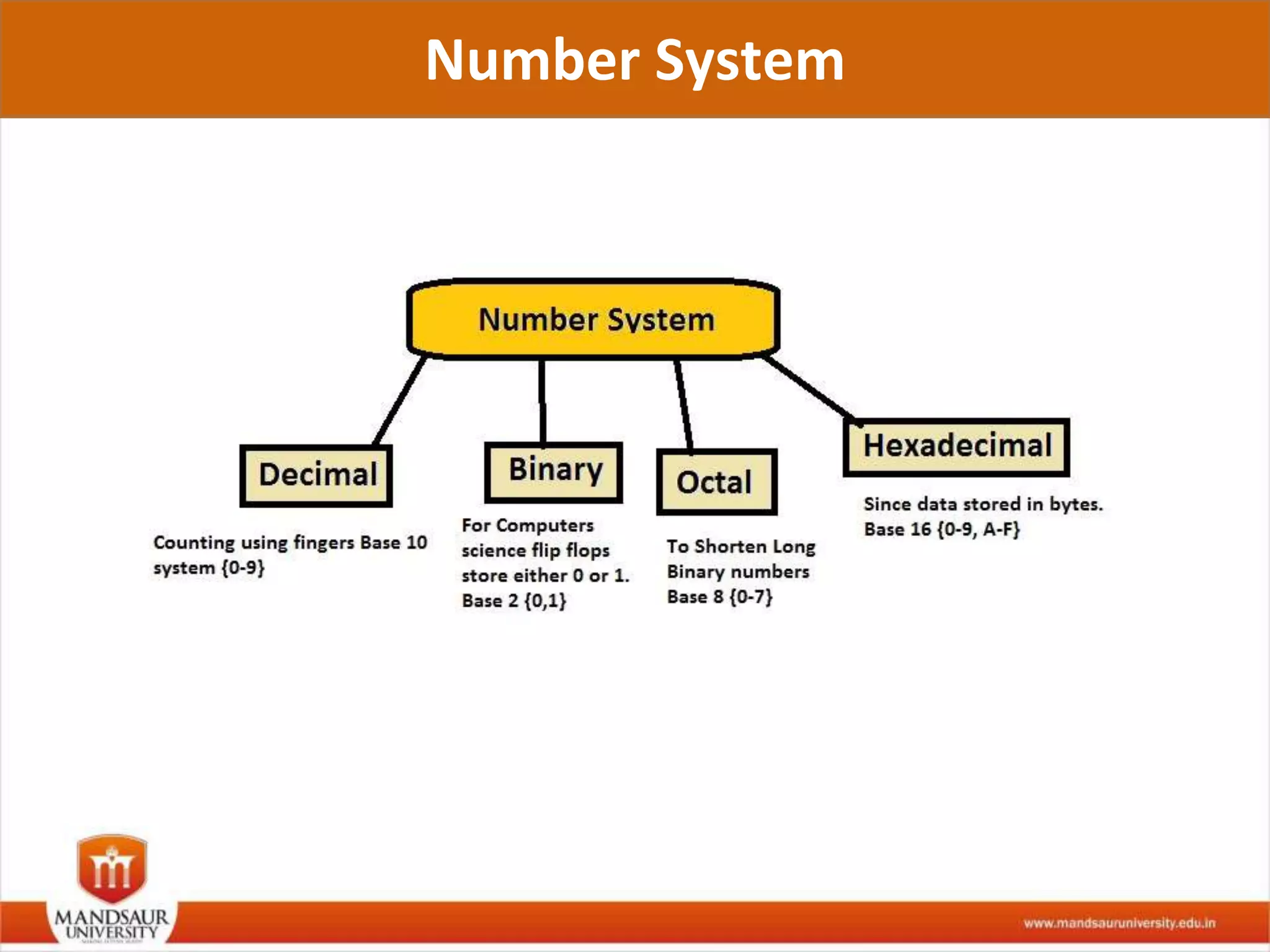
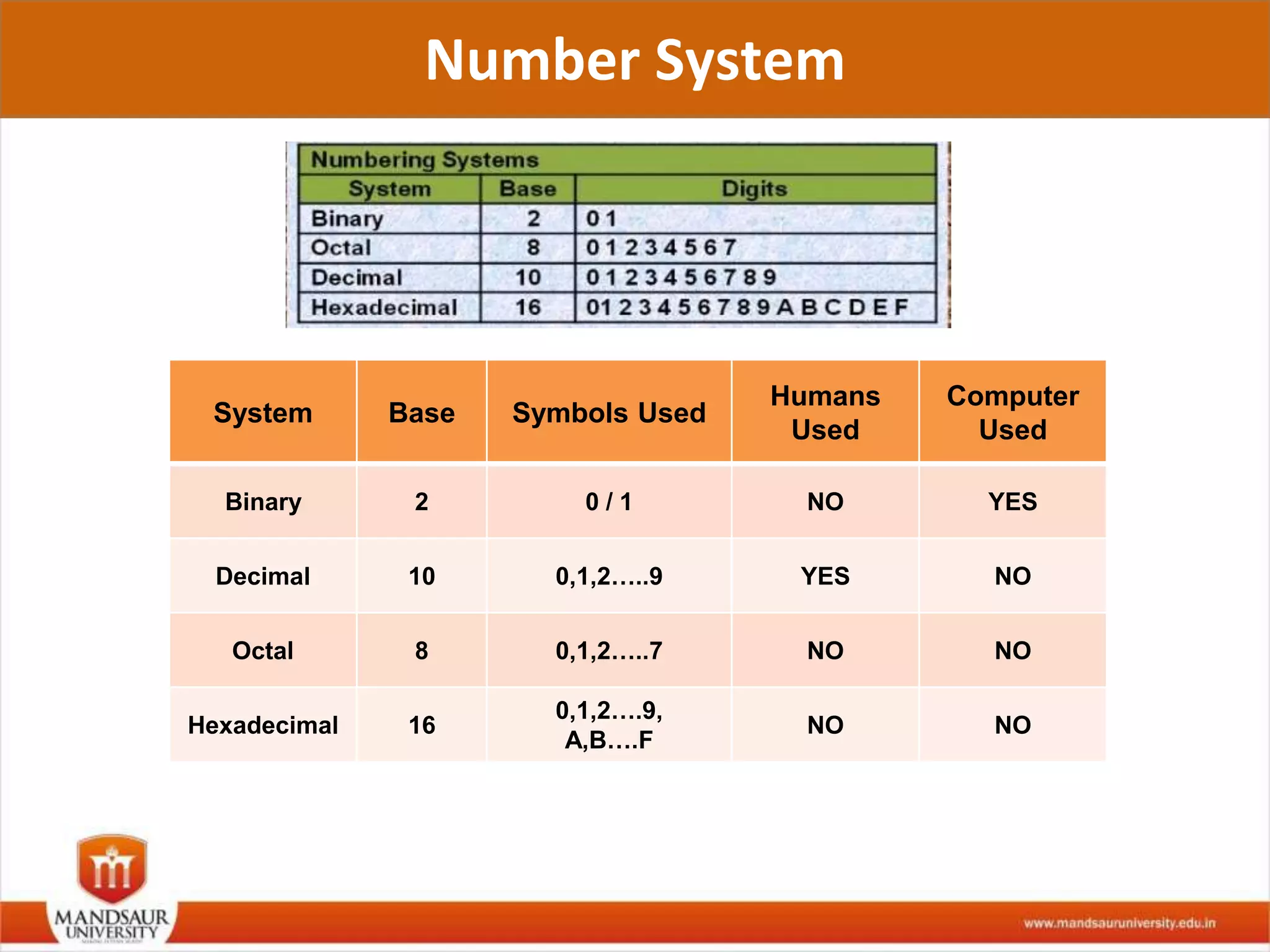
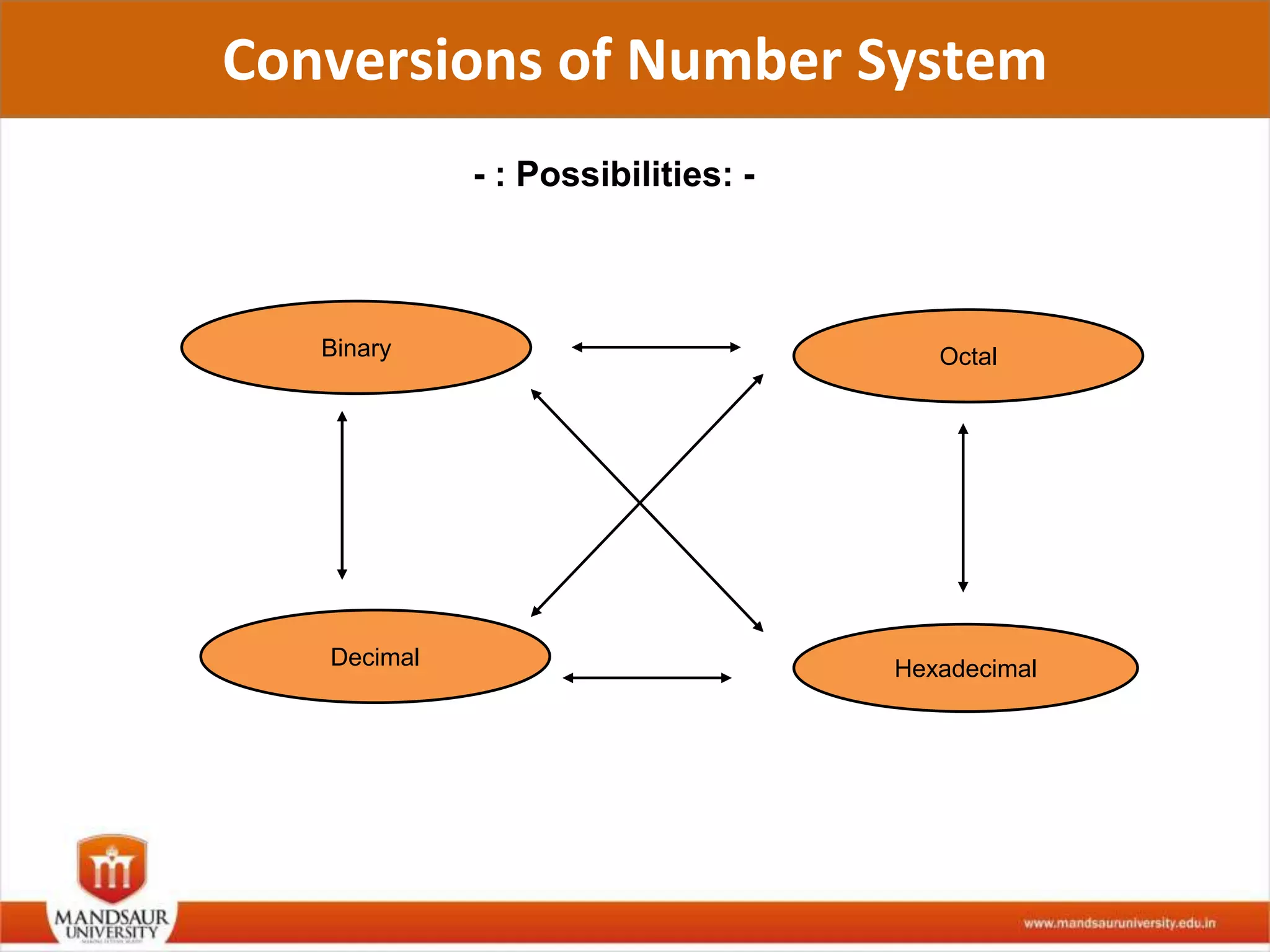
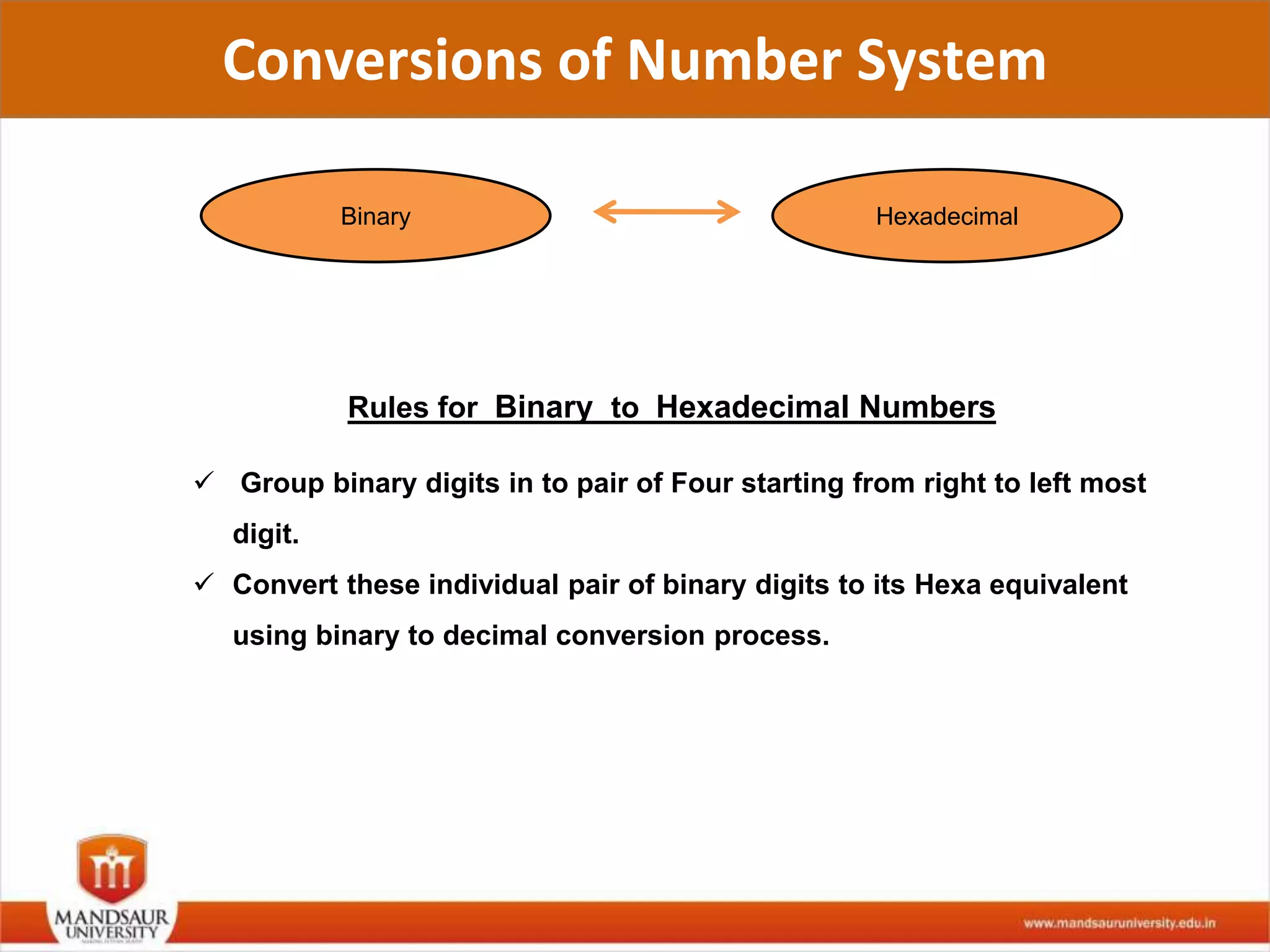
The document discusses different number systems used in computers such as binary, decimal, octal and hexadecimal. It provides examples and techniques for converting between these number systems. The key number systems covered are binary, which uses two digits (0 and 1), and is used in computers, decimal which uses 10 digits and is used in everyday life, octal which uses 8 digits, and hexadecimal which uses 16 digits and letters A-F. The document also discusses techniques for converting fractions between decimal and binary.

1. DEPARTMENT OF COMPUTER
SCIENCE & APPLICATIONS
BCA070 – DIGITAL ELECTRONICS
By: Prof. Ram Pratap Singh

2. Number System
• Role of Numbers in Computer
• Types of Number System
 Binary Number system
Decimal Number system
Octal Number system
Hexadecimal Number system

3. Binary Number System:
• A positional number system
• Has only 2 symbols or digits (0 and 1). Hence its base = 2
• The maximum value of a single digit is 1 (one less than the value of the base)
• Each position of a digit represents a specific power of the base (2)
• This number system is used in computers
Example
101012 (101100)2 111112
Bit
• Bit stands for binary digit
• A bit in computer terminology means either a 0 or a 1
• A binary number consisting of n bits is called an n-bit number
Number System

4. Number System
Decimal Number System
• A positional number system
• Has 10 symbols or digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Hence, its base = 10
• The maximum value of a single digit is 9 (one less than the value of the base).
• Each position of a digit represents a specific power of the base (10)
• We use this number system in our day-to-day life
Example- 258610 (2586)10
258610 = (2 x 103) + (5 x 102) + (8 x 101) + (6 x 100)
= 2000 + 500 + 80 + 6

5. Number System
Octal Number System
• A positional number system
• Has total 8 symbols or digits (0, 1, 2, 3, 4, 5, 6, 7) Hence, its base = 8
• The maximum value of a single digit is 7 (one less than the value of the base
• Each position of a digit represents a specific power of the base (8)
Example- 15068 (2016)8

6. Number System
Hexadecimal Number System
• A positional number system
• Has total 16 symbols or digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Hence its base = 16
• The symbols A, B, C, D, E and F represent the decimal values 10, 11, 12, 13,
14 and 15 respectively
• The maximum than the value of a single of the base)
Example- 15A616 (FACE)16

7. Number System

8. Number System
System Base Symbols Used
Humans
Used
Computer
Used
Binary 2 0 / 1 NO YES
Decimal 10 0,1,2…..9 YES NO
Octal 8 0,1,2…..7 NO NO
Hexadecimal 16
0,1,2….9,
A,B….F
NO NO

9. Conversions of Number System
- : Possibilities: -
Decimal
OctalBinary
Hexadecimal

10. Conversions of Number System
12510 =>
Weight
Base
Binary to Decimal
Rules
 Multiply the each bit start from right to left most digit by its base value with the
power of n, where n is the weight of the bit.
 weight is just a position of a particular bit. Which counts from 0 to places at
the end of right side.
 And lastly we add the results.
5 x 100 = 5
2 x 101 = 20
1 x 102 = 100
125

11. Conversions of Number System
Example
1010112 => 1 x 20 = 1
1 x 21 = 2
0 x 22 = 0
1 x 23 = 8
0 x 24 = 0
1 x 25 = 32
4310
(101011)2 = (43)10

12. Conversions of Number System
Decimal to Binary
 Divide the decimal number to be converted by 2.
 Record the remainder.
 the rightmost the new base digit (least significant digit) of number.
 Divide the quotient of the previous divide by same base i.e. 2.
 Record the remainder from above Step.
 Recording remainders from right to left, until the quotient becomes zero.
 Note that the last remainder thus new obtained will be the most significant
digit (MSD) of the base number.

13. Conversions of Number System
Decimal to Binary
Example:
12510 = ?2
2 125
62 1
2
15 1
2
31 0
2
7 12
3 12
1 12
0 1
LSB
MSB
12510 = 11111012
Remainder

14. Conversions of Number System
Octal
Binary
Decimal
Rules for Binary to Octal Numbers
 First Divide all given binary digits in to pair of three starting from
right to left most digit.
 if there is any bit short then use zero’s to complete the pair of three
as per above step.
 Convert these individual pair of binary digits to its octal equivalent
using binary to decimal process.

15. Conversions of Number System
Example: 11010102 = ?8
 Divide the binary digits into groups of three from right.
1101010
001 101 010
 Convert each group into one octal digit.
0012 1012 0102
= 0 x 22 + 0 x 21 + 1 x 20 1 x 22 + 0 x 21 + 1 x 20 0 x 22 + 1 x 21 + 0 x 20
= 0 + 0 + 1 4 + 0 + 1 0 + 2 + 0
= 1 5 2
(1101010)2 = (152)8

16. Conversions of Number System
10110101112 = ?8
1 011 010 111
1 3 2 7
10110101112 = 13278
Cont.....

17. Conversions of Number System
HexadecimalBinary
Rules for Binary to Hexadecimal Numbers
 Group binary digits in to pair of Four starting from right to left most
digit.
 Convert these individual pair of binary digits to its Hexa equivalent
using binary to decimal conversion process.

18. Conversions of Number System
Example: 11010102 = ?16
 Divide the binary digits into groups of four from right.
01101010
0110 1010
 Convert each group into one Hexa digit.
01102 10102
= 0 x 23 + 1 x 22 + 1 x 21 + 0 x 20 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20
= 0 + 4 + 2 + 0 8 + 0 + 2 + 0
= 6 10
(1101010)2 = (6A)16

19. Conversions of Number System
10101110112 = ?16
10 1011 1011
10101110112 = 2BB16
Cont.....
2 B B

20. Conversions of Number System
Converting a Decimal Number to a Number of Another Base
Division-Remainder Method
Step 1: Divide the decimal number to be converted by the value of the new base.
Step 2: Record the remainder from Step 1 as the rightmost the new base digit (least
significant digit) of number.
Step 3: Divide the quotient of the previous divide by the new base .
Step 4: Record the remainder from Step 3 as the next digit (to the left) of the new base
number.
 Repeat Steps 3 and 4, recording remainders from right to left, until the quotient
becomes zero in Step 3
 Note that the last remainder thus new obtained will be the most significant digit
(MSD) of the base number

21. Decimal to Octal
Example
95210 = ?8
Solution:
8 952 Remainders
8 119 0
8 14 7
1 6
Hence, 95210 = 16708

22. Decimal to Octal
Example
123410 = ?8
Solution:
8 1234 Remainders
8 154 2
8 19 2
02 3
Hence, 123410 = 23228

23. Octal to Decimal
Converting a Number of Another Base to a
Decimal Number
Rules:
Step 1: Determine the column (positional) value of each digit.
Step 2: Multiply the obtained column values by the digits in the
corresponding columns.
Step 3: Calculate the sum of these products.
Example:
47068 = ?10
47068 = 4 x 83 + 7 x 82 + 0 x 81 + 6 x 80
= 4 x 512 + 7 x 64 + 0 + 6 x 1
= 2048 + 448 + 0 + 6
= 250210

24. Hexadecimal to Decimal
Example:
47B16 = ?10
47B16 = 4 x 162 + 7 x 161 + 11 x 160
= 4 x 256 + 7 x 16 + 11 x 1
= 1024 + 112 + 11
= 114710
47B16 = 114710

25. CONVERSION
Converting a Number of Some Base to a Number of Another Base
Example
5456 = ?4
Solution:
Step 1: Convert from base 6 to base 10
5456 = 5 x 62 + 4 x 61 + 5 x 60
= 5 x 36 + 4 x 6 + 5 x 1
= 180 + 24 + 5 = 20910
Step 2: Convert 20910 to base 4
4 209 Remainder
4 52 1
4 13 0
4 3 1
0 3
Hence, 20910 = 31014
So, 5456 = 20910 = 31014
Thus, 5456 = 31014

26. Conversions of Number System
Octal to Binary
Technique:
Convert each octal digit to a 3-bit equivalent binary representation
Example:
7058 = ?2
7 0 5
111 000 101
7058 = 1110001012

27. Conversions of Number System
Hexadecimal to Binary
Technique:
Convert each octal digit to a 4-bit equivalent binary representation
Example:
70516 = ?2
7 0 5
0111 0000 0101
7058 = 0111000001012

28. Hexadecimal to Binary
Example:
10AF16 = ?2
1 0 A F
0001 0000 1010 1111
10AF16 = 00010000101011112

29. Octal to Hexadecimal
• Technique
– Use binary as an intermediary
Example:
10768 = ?16
1 0 7 6
001 000 111 110
2 3 E
10768 = 23E16

30. Hexadecimal to Octal
• Technique
– Use binary as an intermediary
Example:
1F0C16 = ?8
1 F 0 C
0001 1111 0000 1100
1 7 4 1 4
1F0C16 = 174148

31. Conversions of Number System
Fractions
• Binary to decimal
10.1011 =>
1 x 21 = 2.0
0 x 20 = 0.0
1 x 2-1 = 0.5
0 x 2-2 = 0.0
1 x 2-3 = 0.125
1 x 2-4 = 0.0625
(2.6875)10

32. Conversions of Number System
Fractions
• Decimal to binary
3.14579
.14579
x 2
0.29158
x 2
0.58316
x 2
1.16632
x 2
0.33264
x 2
0.66528
x 2
1.33056
etc.11.001001...