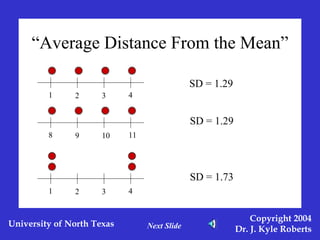
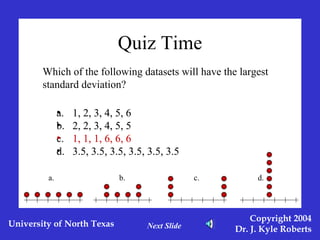
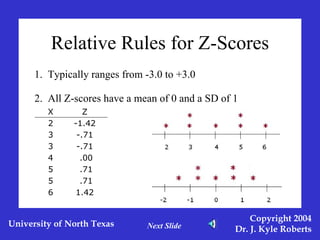
This document discusses different measures of spreadoutness in statistics, including range, standard deviation, z-scores, and standard error of the mean. It explains that range is the simplest measure but has limitations, while standard deviation measures how far scores are from the mean in the data's own units. Z-scores indicate an individual score's distance from the mean in units of standard deviations and allow comparison across data sets with different means and standard deviations. The standard error of the mean represents sampling error and is used to construct confidence intervals.

1. Unit 1: Background to Inferential Statistics Lesson 4: Measures of Spreadoutness EDER 6010: Statistics for Educational Research Dr. J. Kyle Roberts University of North Texas Next Slide

2. Measures of Spreadoutness Range Standard Deviation Z-scores Standard Error of the Mean Next Slide

3. Range “ The simplest measure of spreadoutness” The number of units on the scale of measurement that include the highest and lowest values Range = (X Highest – X Lowest ) + 1 X = 1,2,3,4,5 Range = (5 – 1) +1 = 5 X = -1,-2,-3,-4,-5 Range = ((-1) – (-5)) +1 = 4 + 1 = 5 Next Slide

4. Problems with Range It only considers two scores: Study 2: X = 1, 2, 3, 4, 5 Range = 5 Study 3: X = 1,1,1,1,1,5,5,5,5,5 Range = 5 Study 4: X = 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,5 Range = 5 Study 1: X = 1, 5 Range = 5 Next Slide

5. Standard Deviation “ A measure of spreadoutness in the data’s own metric” Next Slide where: is each person’s individual score is the mean of all scores n is the number of people in the study

6. Computing the SD X = 1, 2, 3, 4 SD = 1.29 Next Slide

7. “ Average Distance From the Mean” SD = 1.29 SD = 1.29 SD = 1.73 Next Slide 1 2 3 4 8 9 10 11 1 2 3 4

8. Quiz Time Which of the following datasets will have the largest standard deviation? 1, 2, 3, 4, 5, 6 2, 2, 3, 4, 5, 5 1, 1, 1, 6, 6, 6 3.5, 3.5, 3.5, 3.5, 3.5, 3.5 1, 2, 3, 4, 5, 6 2, 2, 3, 4, 5, 5 1, 1, 1, 6, 6, 6 3.5, 3.5, 3.5, 3.5, 3.5, 3.5 Next Slide a. b. c. d.

9. Z-Scores A measure of spreadoutness for individuals. 2 Studies Study 1 Study 2 Johnny scored 5 points above the mean Susan scored 9 points above the mean Who did better in relationship to their fellow classmates? Next Slide

10. Computing Z-Scores How far that person is from the mean Relative to the standard deviation Next Slide

11. The 2 Studies Mean = 10 SD = 2 Mean = 10 SD = 9 Z Johnny = +2.5 Z Susan = +1.0 Next Slide Study 1 Study 2 Johnny scored 5 points above the mean Susan scored 9 points above the mean Who did better in relationship to their fellow classmates?

12. Relative Rules for Z-Scores 1. Typically ranges from -3.0 to +3.0 2. All Z-scores have a mean of 0 and a SD of 1 Next Slide X 2 3 3 4 5 5 6 Z -1.42 -.71 -.71 .00 .71 .71 1.42

13. Standard Error of the Mean “The Standard Deviation of the Sampling Distribution” Standard Deviation of X Number of people in the study Used in the construction of “Confidence Intervals” Next Slide

14. Unit 1: Background to Inferential Statistics Lesson 4: Measures of Spreadoutness EDER 6010: Statistics for Educational Research Dr. J. Kyle Roberts University of North Texas