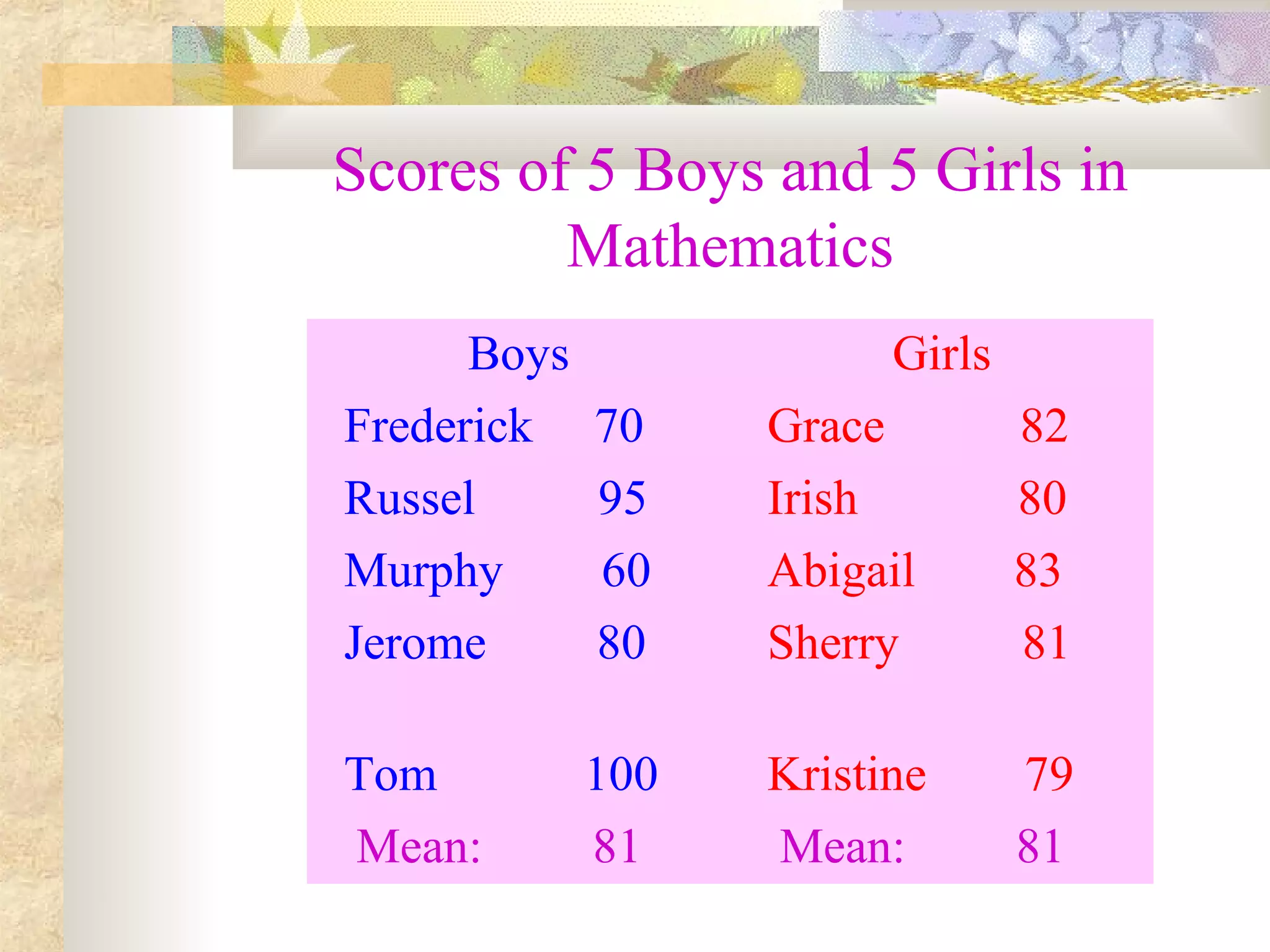
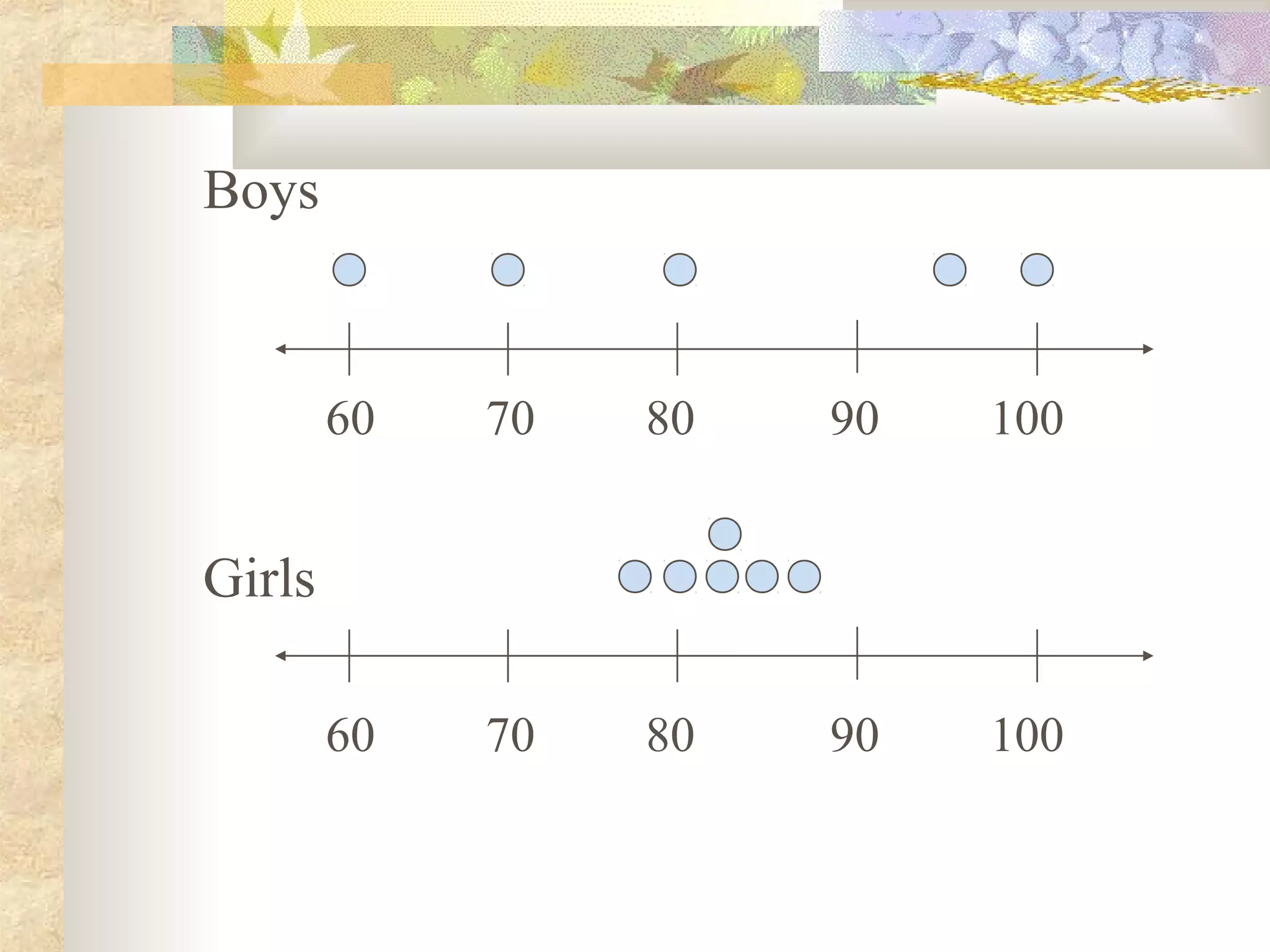
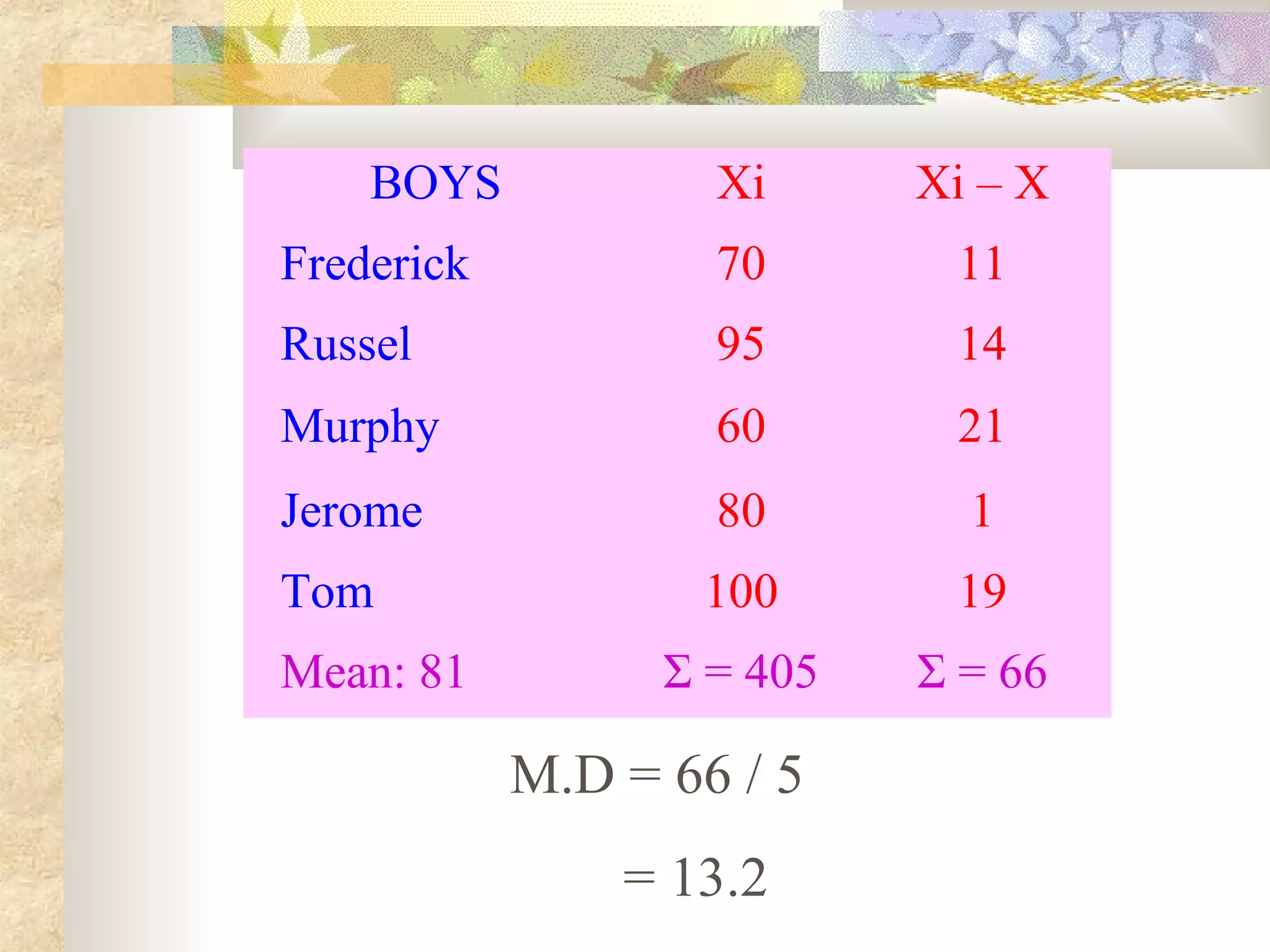
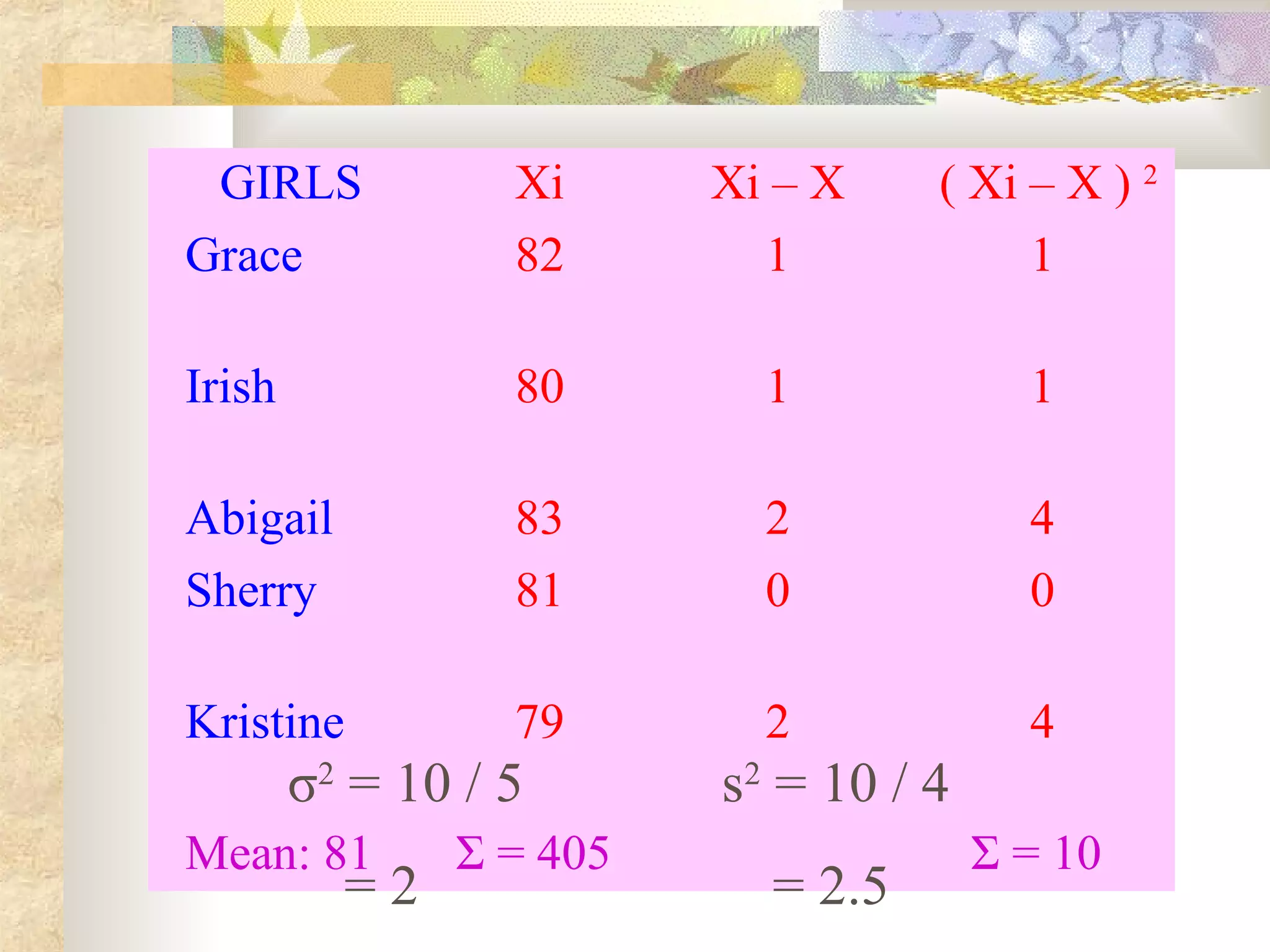
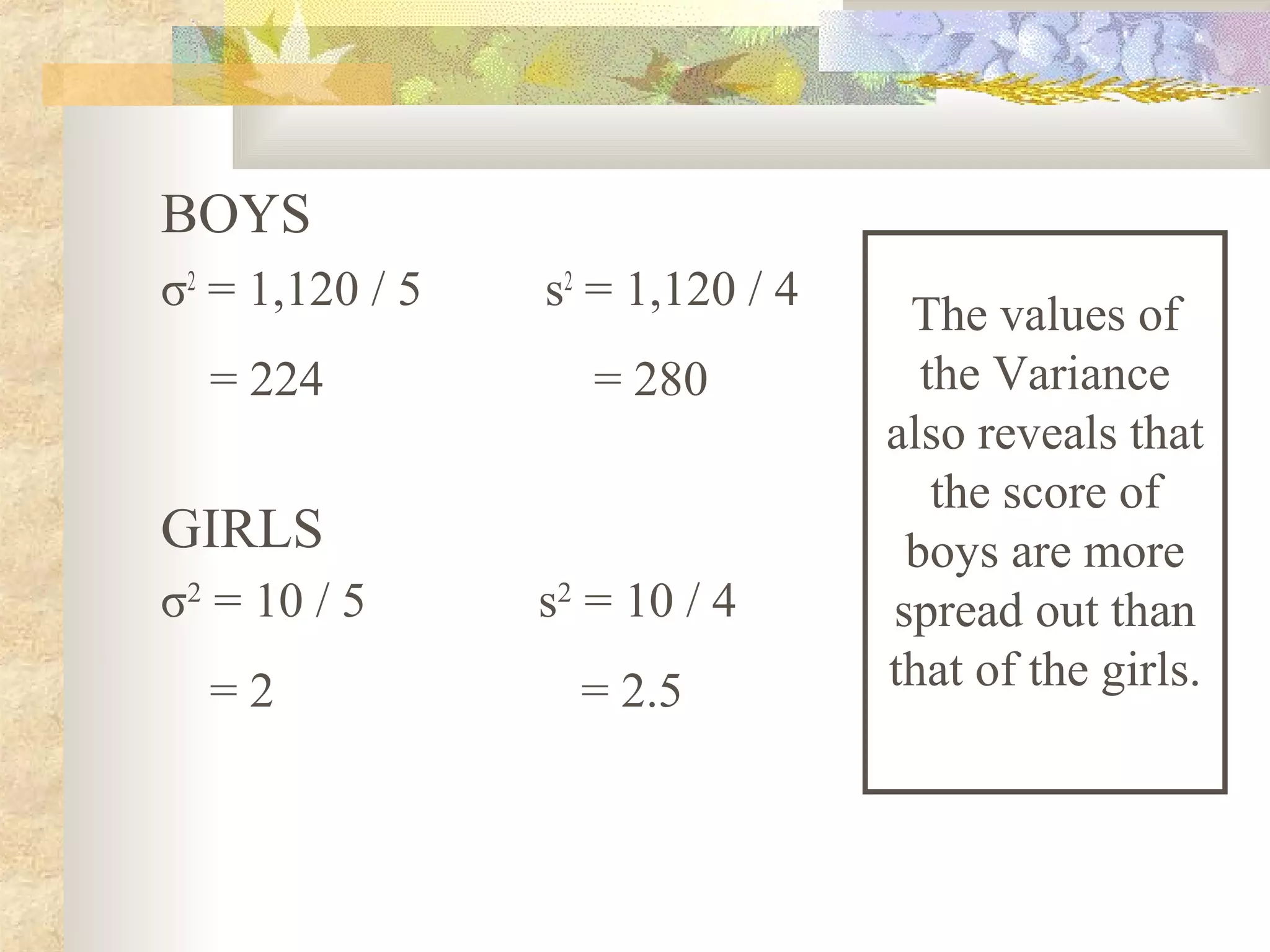The document outlines objectives for students to learn about measures of variability, including range, mean deviation, variance, and standard deviation. It provides examples of calculating each measure for two data sets of boys' and girls' math scores. The results show the girls' data is more homogeneous, as the measures of variability are lower for the girls' data than the boys' data.

1. OBJECTIVES:
During the period, the students are
expected to:
1. identify the different Measures of
Variability;
2. give the formula to compute each
Measure of Variability;
3. solve problems involving Measures of
Variability ( ungrouped data ).

2. Boys Girls
Frederick 70 Grace 82
Russel 95 Irish 80
Murphy 60 Abigail 83
Jerome 80 Sherry 81
Tom 100 Kristine 79
Mean: 81 Mean: 81
Scores of 5 Boys and 5 Girls in
Mathematics

3. Boys
60 70 80 90 100
Girls
60 70 80 90 100

4. Measures of
Variability or
Dispersion

5. RANGE:
The difference between the highest and the
lowest observation
R = H – L
Boys: R = 100 – 60
R = 40
Girls: R = 83 – 79
R = 4
Therefore the
girls are more
homogeneous
than the boys in
their math
ability

6. Mean Deviation:
The average of the summation of the
absolute deviation of each observation
from the mean.
MD = Σ Xi - X
n

7. BOYS Xi Xi – X
Frederick 70 11
Russel 95 14
Murphy 60 21
Jerome 80 1
Tom 100 19
Mean: 81 Σ = 405 Σ = 66
M.D = 66 / 5
= 13.2

8. GIRLS Xi Xi – X
Grace 82 1
Irish 80 1
Abigail 83 2
Sherry 81 0
Kristine 79 2
Mean: 81 Σ = 405 Σ = 6
M.D = 6 / 5
= 1.2

9. MD ( boys ) = 13.2
MD ( girls ) = 1.2
- based from the computed Mean
Deviation, the girls are more
homogeneous than the boys.

10. VARIANCE:
The average of the squared deviation
from the mean.
Population Variance
σ 2
= Σ ( Xi – X ) 2
n
Sample Variance
s 2
= Σ ( Xi – X ) 2
n - 1

11. BOYS Xi Xi – X ( Xi – X ) 2
Frederick 70 -11 121
Russel 95 14 196
Murphy 60 -21 441
Jerome 80 -1 1
Tom 100 19 361
Mean: 81 Σ = 405 Σ = 1,120
σ2
= 1,120 / 5 s2
= 1,120 / 4
= 224 = 280

12. GIRLS Xi Xi – X ( Xi – X ) 2
Grace 82 1 1
Irish 80 1 1
Abigail 83 2 4
Sherry 81 0 0
Kristine 79 2 4
Mean: 81 Σ = 405 Σ = 10
σ2
= 10 / 5 s2
= 10 / 4
= 2 = 2.5

13. BOYS
σ2
= 1,120 / 5 s2
= 1,120 / 4
= 224 = 280
GIRLS
σ2
= 10 / 5 s2
= 10 / 4
= 2 = 2.5
The values of
the Variance
also reveals that
the score of
boys are more
spread out than
that of the girls.

14. STANDARD DEVIATION:
The square root of the Variance
BOYS
σ 2
= 224 s 2
= 280
σ = 14.97 s = 16.73
GIRLS
σ 2
= 2 s 2
= 2.5
σ = 1.41 s = 1.58

15. Question:
Why do you think the
RANGE is considered an
unreliable Measure of
Variability?

16. Answer:
The RANGE is considered
unreliable because we will only
use two values, the highest and the
lowest which is not a complete
representation of all the
observations.

17. Think about this:
Why do we need to work
harmoniously with
everyone?

18. Recap:
 What are the different
Measures of Variability?
 How do we compute for each
measure?

19. SEATWORK:
Given the table below, compute for R,
MD, s, and s2
Xi l Xi – X l ( Xi – X ) 2
17
15
22
19
18
Σ = Σ = Σ =

20. Xi l Xi – X l ( Xi – X ) 2
17 1.2 1.44
15 3.2 10.24
22 3.8 14.44
19 0.8 0.64
18 0.2 0.04
Σ = 91 Σ = 9.2 Σ = 26.8

21. 1. Range = 7
2. MD = 1.84
3. s = 2.59
σ = 2.32
4. s 2
= 6.7
σ 2
= 5.36