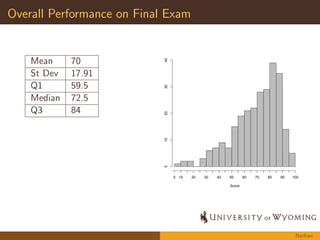
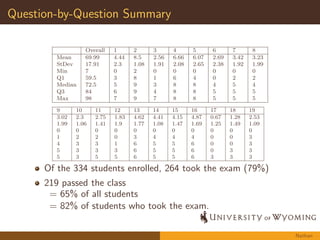
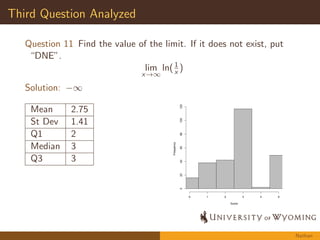
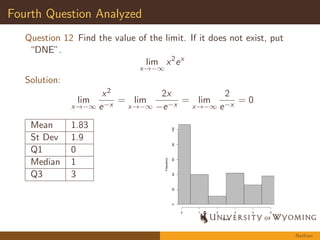
The document summarizes an assessment study conducted on student performance in Calculus I at a university. It describes the motivation, methods, and key findings of the study. The study analyzed student work on four exam questions to assess understandings of calculus concepts. Overall, students demonstrated understanding of integrals as areas under curves but struggled with formal limit notation. On a substitution problem, most students could apply the technique but had difficulties determining antiderivatives. The study provides insight into student learning outcomes in Calculus I.

1. What do students at UW get out of Calculus I?
Work for the Assessment Committee
Dr. Michelle Chamberlin, Dr. Nathan Clements
November, 13th, 2014

2. Agenda
1 Methods and context for the study
2 Students overall performance on the

3. nal exam
3 Results for four exam questions
4 Conclusions and next steps
5 Questions and discussion
Michelle

4. Motivation for the study
Each year we are required to assess the learning of our
undergraduate students in mathematics
Needed assessment activities for the 2013-2014 academic year
Decided to draw upon student work that Nathan had
collected in Calculus I
Michelle

5. What is assessment of student learning?
A process that all programs at UW are required to undertake.
Involves an iterative process of:
Posing a question about how well are students learning?
Gathering evidence about students learning
Interpreting and analyzing such evidence
Using the results to enhance teaching and learning within the
program
Repeat
We are asked to engage in such
cycles yearly
Michelle

6. 2013-2014 Assessment Question
Question: What understandings of the basic concepts and skills
from our calculus sequence do students exhibit on the
comprehensive

7. nal exams?
Assesses Objective 1 under Goal 1 of our Undergraduate
Learning Goals and Objectives
Goal 1: Students shall demonstrate a solid understanding
appropriate for the 1000- and 2000-level mathematics required
in their majors.
Objective 1: Show pro

8. ciency in basic skills and concepts
embedded in their courses
Michelle

9. Data Collected: Student Work on Final Exam
To target our eorts, we elected to focus on Calculus I
Students take a comprehensive and common

10. nal
Decided to analyze students work on selected questions from
the

11. nal exam
Provide a picture of student learning across dierent sections
and instructors
In Fall 2013, scanned student work on the

12. nal exam and
entered students overall scores and scores on each question
into a spreadsheet
To select speci

13. c exam items, we looked for questions with a
spread of scores
We selected 4 questions from the

14. nal exam to analyze
Michelle

15. Analysis of Student Work on Exam Questions
For each question:
1 Randomly sampled work from approximately 35 students
2 Articulated the procedures, skills, and understandings that
were associated with each question
3 Read through students work, coding common approaches,
dierent ways of thinking, and errors
4 Generated frequency information about the dierent
approaches, ways of thinking, and errors
5 Prepared an overall conclusion about students learning
Michelle

16. Overall Performance on Final Exam
Mean 70
St Dev 17.91
Q1 59.5
Median 72.5
Q3 84
Q1 59.5 3 8 1 6 4 0 2 Median 72.5 5 9 3 8 8 4 5 Q3 84 6 9 4 8 8 5 5 Max 98 7 9 7 8 8 5 5 All Scores (all sections)
Score
Frequency
0 10 20 30 40
5 10 20 30 40 50 60 70 80 90 100
Problem: 2 (all sections)
150 200
50 60
Nathan

17. Question-by-Question Summary
Math 2200 Exam 4 – All Sections
Fall 2013
Overall 1 2 3 4 5 6 7 8 9 10 11 Mean 69.99 4.44 8.5 2.56 6.66 6.07 2.69 3.42 3.23 3.02 2.3 2.75 StDev 17.91 2.3 1.08 1.91 2.08 2.65 2.38 1.92 1.99 1.99 1.06 1.41 Min 7 0 2 0 0 0 0 0 0 0 0 0 Q1 59.5 3 8 1 6 4 0 2 2 1 2 2 Median 72.5 5 9 3 8 8 4 5 4 4 3 3 Q3 84 6 9 4 8 8 5 5 5 5 3 3 Max 98 7 9 7 8 8 5 5 5 5 3 5 All Scores (all sections)
Math 2200 Exam 4 – All Sections
Of the 334 students enrolled, 264 took the exam (79%)
219 passed the class
= 65% of all students
= 82% of students who took the exam.
Frequency
10 20 30 40
Fall 2013
6 7 8 9 10 11 12 13 14 15 16 17 18 19
2.69 3.42 3.23 3.02 2.3 2.75 1.83 4.62 4.41 4.15 4.87 0.67 1.28 2.53
2.38 1.92 1.99 1.99 1.06 1.41 1.9 1.77 1.08 1.47 1.69 1.25 1.49 1.09
0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 2 2 1 2 2 0 3 4 4 4 0 0 3
4 5 4 4 3 3 1 6 5 5 6 0 0 3
5 5 5 5 3 3 3 6 5 5 6 0 3 3
5 5 5 5 3 5 5 6 5 5 6 3 3 3
Problem: 1 (all sections)
60
Nathan

18. First Question Analyzed
Question 3 Express the integral below as a limit of Riemann sums.
Do not evaluate. Z
0
sin(5x)dx
Solution lim
n!1
Xn
i=1
sin
5i
n
n
Michelle

19. 1st Q: Understandings and Procedures {
R
0 sin(5x)dx
A de

20. nite integral represents the area under the curve
between two given xvalues (a and b).
We often use a sum of the areas of rectangles to approximate
the integral.
This approximation is more accurate as we use rectangles with
smaller widths
The value of the integral is found by computing the limit as
these widths go to zero, i.e., as the given segment along the
xaxis is broken into more and more (an in

21. nite number) of
subintervals.
The width of each rectangle is given by (b a)=n where n is
the number of partitions and is represented by x.
The height of each rectangle is found by evaluating the
function at any point within each subinterval (x
i )
Z b
Thus,
a
f (x)dx = lim
n!1
Xn
i=1
f (x
i )x
Michelle

22. 1st Q: Understandings and Procedures (cont.) {
R
0 sin(5x)dx
In addition, students need to understand:
How the limit relates to the variable n and how this interfaces
with the variable x
How the summation occurs and relates to the variable i
Limit and summation notation (and function notation)
Michelle

23. 1st Q: Results {
R
0 sin(5x)dx
Of the 264 students completing the exam, 54 earned full credit,
approximately 20%
Of the 35 analyzed:
All but one student understood that an integral represents the
area under the curve, that we use a sum of the areas of
rectangles to approximate this area, and that this is more
accurate when we use more rectangles
34% were able to determine the width and height for each
rectangle in the limit
89% struggled with the concept and formality of expressing
this idea as a limit
This struggle seemed compounded by students diculties with
understanding limit and summation concepts as well as limit,
summation, and function notation
Michelle

24. 1st Q: Common Errors {
R
0 sin(5x)dx
Taking the limit as x goes to in

25. nity, as x goes to n, or as x
goes to
Forgetting to write the limit before the summation notation
Forgetting to multiply by the width of each rectangle
Evaluating the sum from n = 0 to n = or from i = n to
i =
Michelle

26. 1st Question: Conclusion {
R
0 sin(5x)dx
Students appear to be leaving Calculus I with an understanding that:
The integral represents the area under the curve
It is estimated by summing the areas of rectangles, becoming
more accurate with more rectangles
However, they struggle with expressing this idea as a formal
limit
Likely compounded by diculties with limit and summation
concepts as well as associated notation
Michelle

27. Second Question Analyzed
Question 9 Evaluate
Z 1
0
x
(x2 + 1)3 dx
Solution: Requires using integration by substitution where
u = x2 + 1, and so du = 2x dx.
Z 1
0
x
(x2 + 1)3 dx =
3
16
Michelle

28. 2nd Q: Understandings and Procedures {
R 1
0
x
(x2+1)3dx
Procedure Understanding or Skill
Recognize the integrand as
a composed function
Recall substitution as a technique for integrat-
ing a composed function
Identify the associated
compositions of functions:
g(x) = x2 + 1,f (x) = 1=x3,
Being able to decompose a composite function
Selecting and substituting
u = x2 + 1
12
Skillfully selecting a u-substitution such
that its derivative occurs in the integral,
e.g., du = 2xdx, which implies du = xdx
Determine the antideriva-
tive
Application of antidierentiation formulas and
Rproperties of the integral; in particular
un du = 1
n+1un+1 + C; n6= 1
Using appropriate limits of
integration
Understand that with the change of variables,
the coordinate system upon which we are inte-
grating has changed
Apply FTC
R b
a f (x) dx =
F(b)F(a) where F0(x) =
f (x).
Michelle

29. 2nd Q: Results {
R 1
0
x
(x2+1)3dx
Of the 264 students completing the exam, 34% earned full credit.
Of the 35 analyzed:
85% realized the need for u-substitution
However, 89% of these students incorrectly determined the
anti-derivative, often misapplying the anti-dierentiation
formulas
Most students proceeded to evaluate the (often incorrect)
anti-derivative with the correct limits of integration
Michelle

30. 2nd Q: Common Errors {
R 1
0
x
(x2+1)3dx
Failing to realize substitution for du includes the x term
(leaving the x term in the numerator after usubstitution)
Failing to take an antiderivative before evaluating
Challenges with determining the antiderivative:
Misapplication of antidierentiation formulas to numerator and
denominator independently
Perceiving the antiderivative for u3 involves ln
Incorrect use of the Power Rule (subtracting the power by 1
rather than adding one for the antiderivative)
Forgetting to multiply by the coecient of 1
2
Michelle