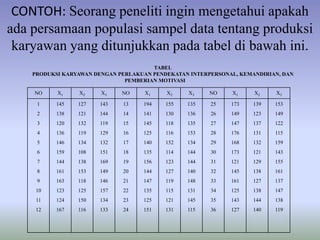
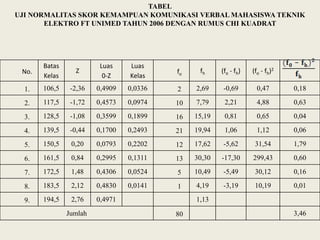
Dokumen tersebut membahas uji persyaratan untuk penelitian, termasuk uji homogenitas, normalitas, dan linieritas. Uji-uji tersebut digunakan untuk mengetahui apakah sampel berasal dari populasi yang sama dan apakah hubungan antara variabel berdistribusi normal serta linier.

1. Uji Persyaratan

2. UJI HOMOGENITAS dengan
Uji Bartlett
•Rumus menghitung varians gabungan :
•Menghitung nilai B dengan rumus:
B = (log s2) ∑( ni – 1)
• Menghitung nilai homogenitas
χ2 = (ln 10) [B - ∑ {(ni – 1) log si
2}]

3. Lanjutan...
KRITERIA PENGUJIAN
HOMOGENITAS :
• Jika : χ2
hitung ≤ χ2
tabel,
Homogen
• Jika : χ2
hitung > χ2
tabel,
Tidak Homogen

4. CONTOH: Seorang peneliti ingin mengetahui apakah
ada persamaan populasi sampel data tentang produksi
karyawan yang ditunjukkan pada tabel di bawah ini.
NO X1 X2 X3 NO X1 X2 X3 NO X1 X2 X3
1
2
3
4
5
6
7
8
9
10
11
12
145
138
120
136
146
159
144
161
163
123
124
167
127
121
132
119
134
108
138
153
118
125
150
116
143
144
119
129
132
151
169
149
146
157
134
133
13
14
15
16
17
18
19
20
21
22
23
24
194
141
145
125
140
135
156
144
147
135
125
151
155
130
118
116
152
114
123
127
119
115
121
131
135
136
135
153
134
144
144
140
148
131
145
115
25
26
27
28
29
30
31
32
33
34
35
36
173
149
147
176
168
173
121
145
161
125
143
127
139
123
137
131
132
121
129
138
127
138
144
140
153
149
122
115
159
143
155
161
137
147
138
119
TABEL
PRODUKSI KARYAWAN DENGAN PERLAKUAN PENDEKATAN INTERPERSONAL, KEMANDIRIAN, DAN
PEMBERIAN MOTIVASI

5. Penyelesaian:
• Berdasarkan tabel 2.3 di Makalah, diperoleh n1 =
n2 = n3 = 36.
• Untuk data X1, adalah:
S1
2 = 317,4
• Untuk data X2, adalah:
S2
2= 141,5
• Untuk data X3, adalah:
S3
2 = 169,3
Besaran-besaran ini dimasukkan dalam Tabel
Besaran yang diperlukan untuk Uji Homogenitas
dengan uji Bartlett.

6. Lanjutan...
• Menghitung besar varians total
= 209,4
 Menghitung satuan B
B = (log s2) ∑( ni – 1)
B = (log 209,4) (105)
B = 243,7
 Menghitung Chi Kuadrat
χ2 = (ln 10) [B - ∑ {(ni – 1) log si
2}]
χ2 = (2,3) [243,7 - 240,8]
χ2 = (2,3) (2,9)
χ2 = 6,6
Bandingkan χ2
hitung dengan nilai χ2
tabel,
untuk α = 0,05 dan derajat kebebasan
(dk) = k = 3 diperoleh χ2
0,95(3) = 7,815.
(χ2 = 6,6 < χ2
0,95(3) = 7,815); berarti
varians populasi sampel penelitian
adalah homogen

7. Uji Normalitas dengan Chi Kuadrat
• Merangkum data seluruh variabel yang akan
diuji.
• Menentukan jumlah kelas interval.
• Menentukan panjang kelas.
• Menyusun ke dalam tabel distribusi frekuensi
(tabel penolong)
• Menghitung frekuensi harapan (fh), dengan
mengalikan persentase luas tiap bidang kurva
normal dengan jumlah anggota sampel.
• Mencari Chi Kuadrat dengan rumus:
χ 2
h = ∑

8. Lanjutan...
• Membandingkan harga Chi Kuadrat hitung dengan Chi
Kuadrat Tabel.
KRITERIA PENGUJIAN NORMALITAS :
Jika : χ2
hitung ≤ χ2
tabel, Normal
Jika : χ2
hitung > χ2
tabel, Tidak Normal

9. CONTOH:
Data hasil penelitian tentang kemampuan komunikasi verbal 80 orang
mahasiswa Teknik Elektro FT Unimed tahun 2006 seperti diperlihatkan
dalam Tabel
167
145
138
115
136
146
159
144
161
163
164
137
124
121
123
124
167
147
173
135
129
151
150
172
157
137
169
139
194
141
145
107
140
135
156
144
173
149
130
156
142
166
147
176
168
173
121
145
161
125
137
140
123
139
162
160
144
138
122
143
145
152
167
124
124
151
163
145
160
172
136
178
170
160
136
129
150
143
139
149

10. Penyelesaian:
• Menentukan skor besar dan kecil:
Skor terbesar = 194
Skor terkecil = 107
• Menentukan rentang:
R = 194 – 107 = 87
• Menentukan banyaknya kelas
K = 1 + 3,3 log n
= 1 + 3,3 log 80 = 1 + 3,3 (1,9) = 1 + 6,28
= 7, 28 dibulatkan = 8
• Menentukan panjang kelas
p = = 10, 875 ≈ 10

11. No. Kelas Interval f Nilai Tengah (X) fx (X – X) (X – X)2 f(X – X)2
1. 107 – 117
2 112 224 -35,1 1229,4 2458,8
2. 118 – 128
10 123 1230 -24,1 579,0 5790,0
3. 129 – 139
16 134 2144 -13,1 170,6 2730,1
4. 140 – 150
21 145 3045 -2,1 4,3 89,3
5. 151 – 161
12 156 1872 8,9 79,9 958,5
6. 162 – 172
13 167 2171 19,9 397,5 5167,6
7. 173 – 183
5 178 890 30,9 957,1 4785,6
8. 184 – 194
1 189 189 41,9 1758,8 1758,8
Jumlah
80 11765 23738,7
TABEL
PERHITUNGAN RATA-RATA DAN SIMPANGAN BAKU
SKOR KEMAMPUAN KOMUNIKASI VERBAL
MAHASISWA TEKNIK ELEKTRO FT UNIMED
TAHUN 2006

12. TABEL
UJI NORMALITAS SKOR KEMAMPUAN KOMUNIKASI VERBAL MAHASISWA TEKNIK
ELEKTRO FT UNIMED TAHUN 2006 DENGAN RUMUS CHI KUADRAT
No.
Batas
Kelas
Z
Luas
0-Z
Luas
Kelas
fo
fh (fo - fh) (fo - fh)2
1. 106,5 -2,36 0,4909 0,0336 2 2,69 -0,69 0,47 0,18
2. 117,5 -1,72 0,4573 0,0974 10 7,79 2,21 4,88 0,63
3. 128,5 -1,08 0,3599 0,1899 16 15,19 0,81 0,65 0,04
4. 139,5 -0,44 0,1700 0,2493 21 19,94 1,06 1,12 0,06
5. 150,5 0,20 0,0793 0,2202 12 17,62 -5,62 31,54 1,79
6. 161,5 0,84 0,2995 0,1311 13 30,30 -17,30 299,43 0,60
7. 172,5 1,48 0,4306 0,0524 5 10,49 -5,49 30,12 0,16
8. 183,5 2,12 0,4830 0,0141 1 4,19 -3,19 10,19 0,01
9. 194,5 2,76 0,4971 1,13
Jumlah 80 3,46

13. Lanjutan...
• Mencari Chi Kuadrat (χ2
h) dengan rumus:
χ2
h = ∑ = 3,46
Membandingkan (χ2
h) dengan (χ2
t), db = k – 3 = 8 – 3 = 5,
maka diperoleh χ 2
0,95(5) = 11,070. Ternyata Chi Kuadrat
hasil perhitungan lebih kecil dari Chi Kuadrat tabel
(χ2
h = 3,46 < χ2
t = 11,070) maka dapat disimpulkan bahwa
data tersebut berdistribusi normal.

14. UJI LINIERITAS
Langkah langkah uji linieritas
• Menyusun tabel kelompok data variabel x dan y ,
dimana variabel x data diurutkan dari yang
terkecil sampai yang terbesar.
• Menghitung jumlah kuadrat regresi JK reg (a)
dengan rumus JK reg (a) =
• Menghitung nilai a dan b
b = n (∑y) - (∑x) (∑y)
n∑x2–(∑x)2
a = Y – bx

15. Lanjutan...
• Menghitung jumlah kuadrat reg b/a (JK reg b/a) dengan rumus :
JK reg (b/a) = b { ∑xy - ∑x . ∑y }
n
• Menghitung rata-rata jumlah kuadrat regresi a (RJK reg (a)) dengan rumus :
RJK reg (a) = JK reg (a)
• Menghitung jumlah kuadrat residu (JK res) dengan rumus :
JK res = ∑y2 – JK reg (b/a) – JK reg (a)
• Menghitung rata-rata jumlah kuadrat regresi b/a (RJK reg (b/a) ) dengan rumus :
RJK reg (b/a) = JK reg (b/a)
• Menghitung rata-rata jumlah kuadrat residu (RJK res) dengan rumus:
RJK res = JK res
n – 2
• Menghitung jumlah kuadrat eror (JK e) dengan rumus :
JK e = ∑k { ∑y2 – ( ∑ y )2 }
n

16. • Menghitung jumlah kuadrat tuna cocok (JK tc) dengan rumus :
JK tc = JK res – JK e
• Menghitung rata-rata jumlah kuadrat tuna cocok (RJK tc) dengan rumus :
RJK tc = JK tc
k – 2
• Menghitung rata-rata jumlah kuadrat eror (RJK e) dengan rumus :
RJK e= JK e
n – k
• Mencari nilai uji F dengan rumus :
F = RJK tc
RJK e
KRITERIA PENGUJIAN LINIERITAS :
Jika : χ2
hitung ≤ χ2
tabel, Linier
Jika : χ2
hitung > χ2
tabel, Tidak linier
Lanjutan...

17. Contoh: Diketahui Motivasi (X), Hasil Belajar (Y), data disusun seperti
No. X Y X2 Y2 X.Y
1 35 57 1225 3249 1995
2 35 55 1225 3025 1925
3 36 56 1296 3136 2016
4 40 45 1600 2025 1800
5 40 56 1600 3136 2240
6 43 57 1849 3249 2451
7 45 58 2025 3364 2610
8 45 46 2025 2116 2070
9 50 45 2500 2025 2250
10 50 44 2500 1936 2200
11 51 60 2601 3600 3060
12 53 58 2809 3364 3074
13 53 67 2809 4489 3551
14 55 45 3025 2025 2475

18. Penyelesaian:
• JK reg (a) =
= 8092
15
= 654.481 = 43.632,06
15
• b = n (∑xy) - (∑x) (∑y)
n∑x2–(∑x)2
= 15 (37017) – (686)(809)
15.32114 - 6862
= 555255 – 554974
481710 – 470596
= 281 = 0,025 = 0,03
11114
• a = Y – bx
= 53,93 – (0,03 x 45,73)
= 53,93 – 1,37 = 52,56

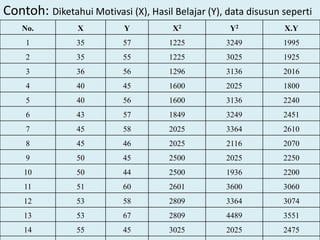
19. Lanjutan...
• Menghitung jumlah kuadrat reg b/a (JK reg b/a) dengan rumus :
JK reg (b/a) = b { ∑xy - ∑x . ∑y }
n
= 0,03 [ 37017 – 686 . 809 ]
15
= 0,03 [ 37017 – 554974 ]
15
= 0,03 [ 37017 – 36998,26 ]
= 0,03 (18,74) = 0,56
• Menghitung rata-rata jumlah kuadrat regresi a (RJK reg (a) ) dengan rumus :
RJK reg (a) = JK reg (a) = 43632,06
• Menghitung jumlah kuadrat residu (JK res) dengan rumus :
JK res = ∑y2 – JK reg (b/a) – JK reg (a)
= 44339 – 0,56 – 43632,06 = 706,38
• Menghitung rata-rata jumlah kuadrat regresi b/a (RJK reg (b/a) ) dengan rumus :
RJK reg (b/a) = JK reg (b/a)
= 0,56

20. • Menghitung rata-rata jumlah kuadrat residu (RJK res) dengan rumus :
RJK res = JK res
n – 2
= 706,38
15 – 2
= 706,38 = 54,34
13
• Menghitung jumlah kuadrat eror (JK e) dengan rumus :
JKe = 2 + 60,5 + 72 + 0,5 + 40,5 + 112,5 = 288
• Menghitung jumlah kuadrat tuna cocok (JK tc) dengan rumus :
JK tc = JK res – JK e
= 706,38 - 288 = 418,38
• Menghitung rata-rata jumlah kuadrat tuna cocok (RJK tc) dengan rumus :
RJK tc = JK tc
k - 2
= 418,38
9 – 2
= 418,38 = 59,77
7
• Menghitung rata-rata jumlah kuadrat eror (RJK e) dengan rumus :
RJK e = JK e
n – k
= 288
15-9
= 288 = 48
6
Lanjutan...

21. Lanjutan...
• Mencari nilai uji F dengan rumus :
F = RJK tc
RJK e
= 59,77 = 1,245 = 1,25
48
Nilai-nilai X semuanya ada 9 yang berbeda, maka k=9
sehingga dk untuk tuna cocok = k – 2 = 9-2=7. Derajat
kebebasan untuk kekeliruan = n - k = 15 - 9 = 6
Jika ᾳ = 0,05, maka dengan dk pembilang 7 dan dk penyebut 6
dari daftar distribusi F didapat F 0,95 (7,6) = 4,21 ( F tabel ). Untuk
uji kelinieran didapat F=1,25 dan ini lebih kecil dari 4,21 Fh <
Ft. Jadi hipotesis bahwa model regresi linier diterima.