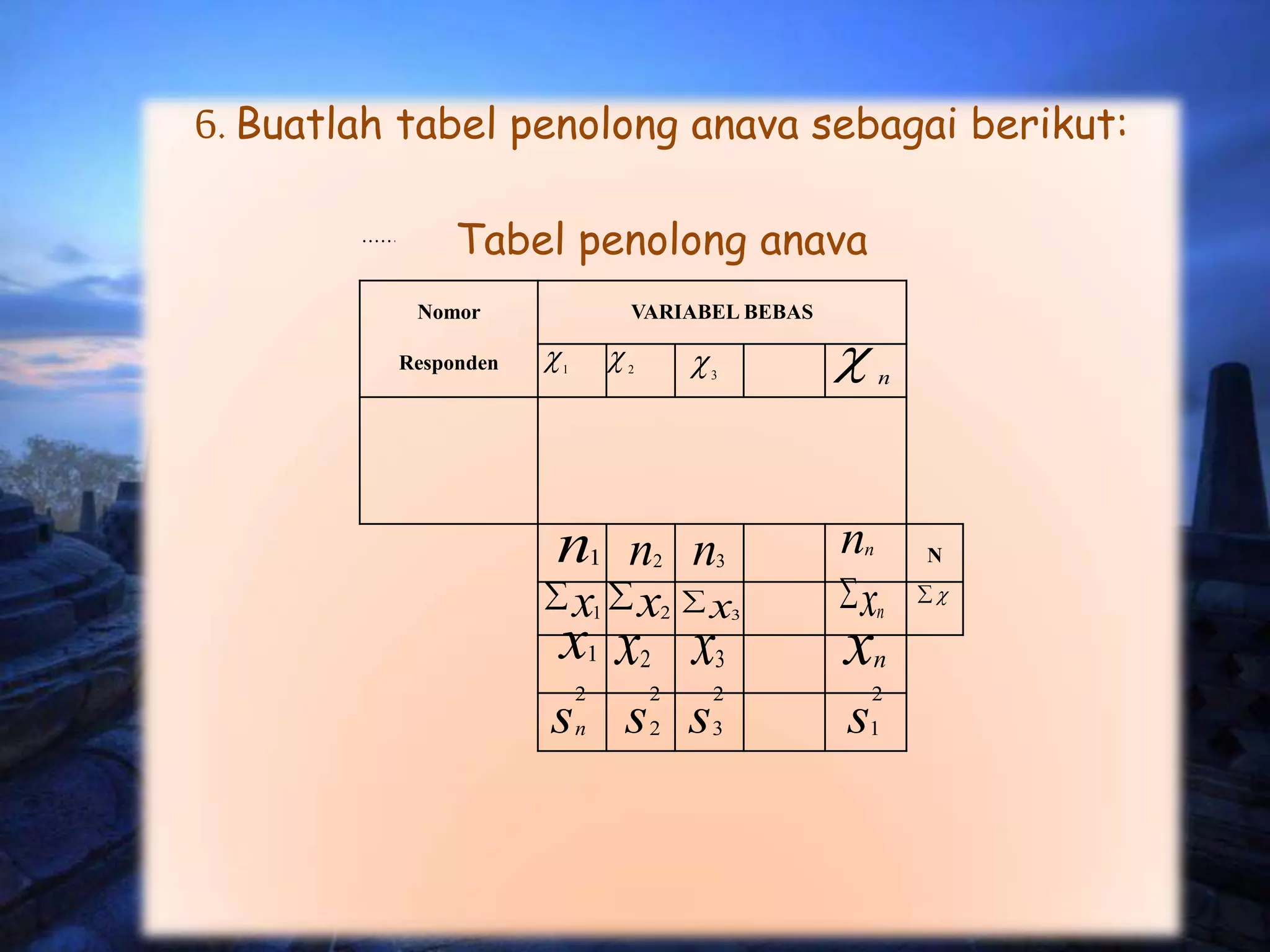
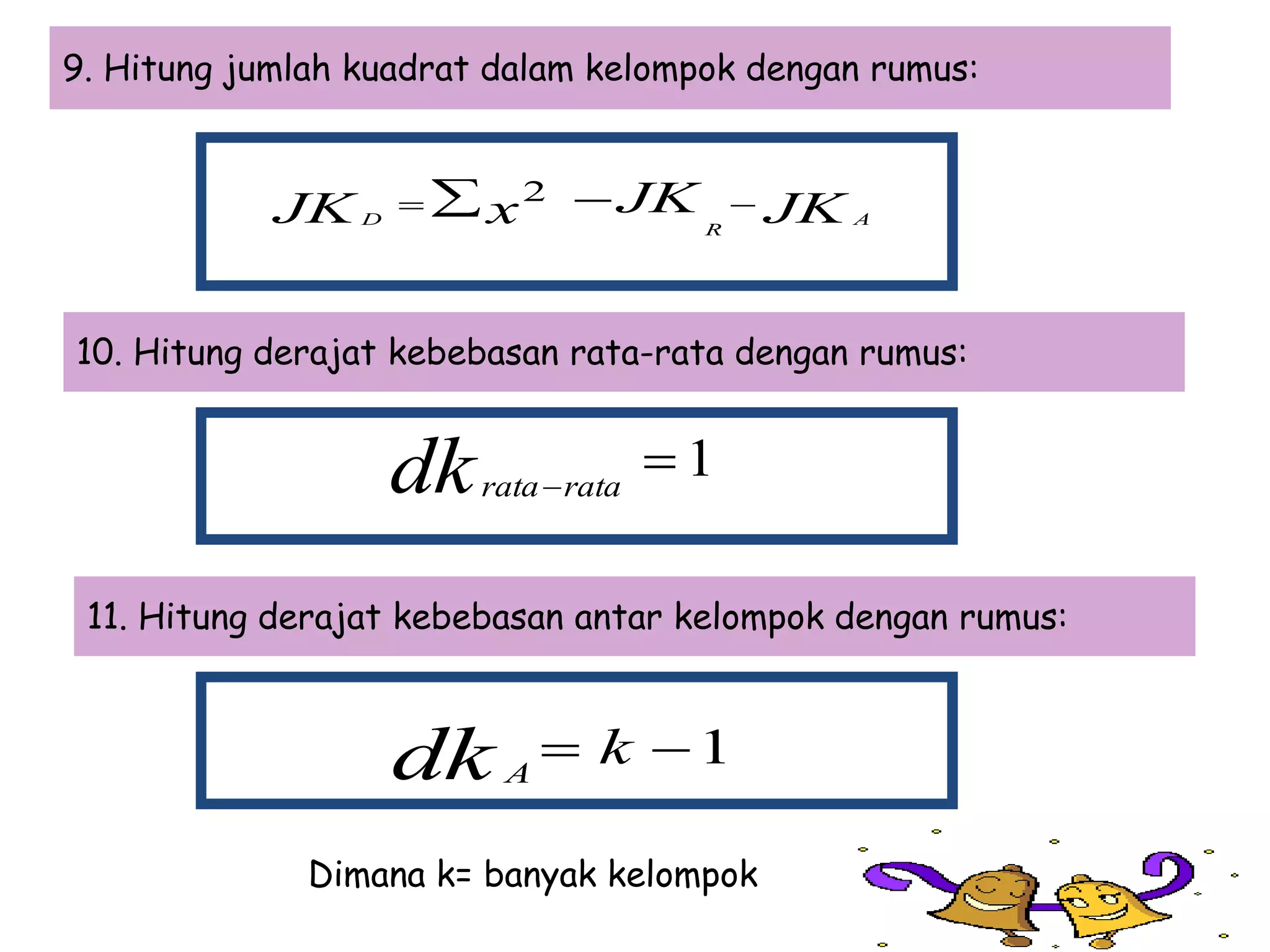
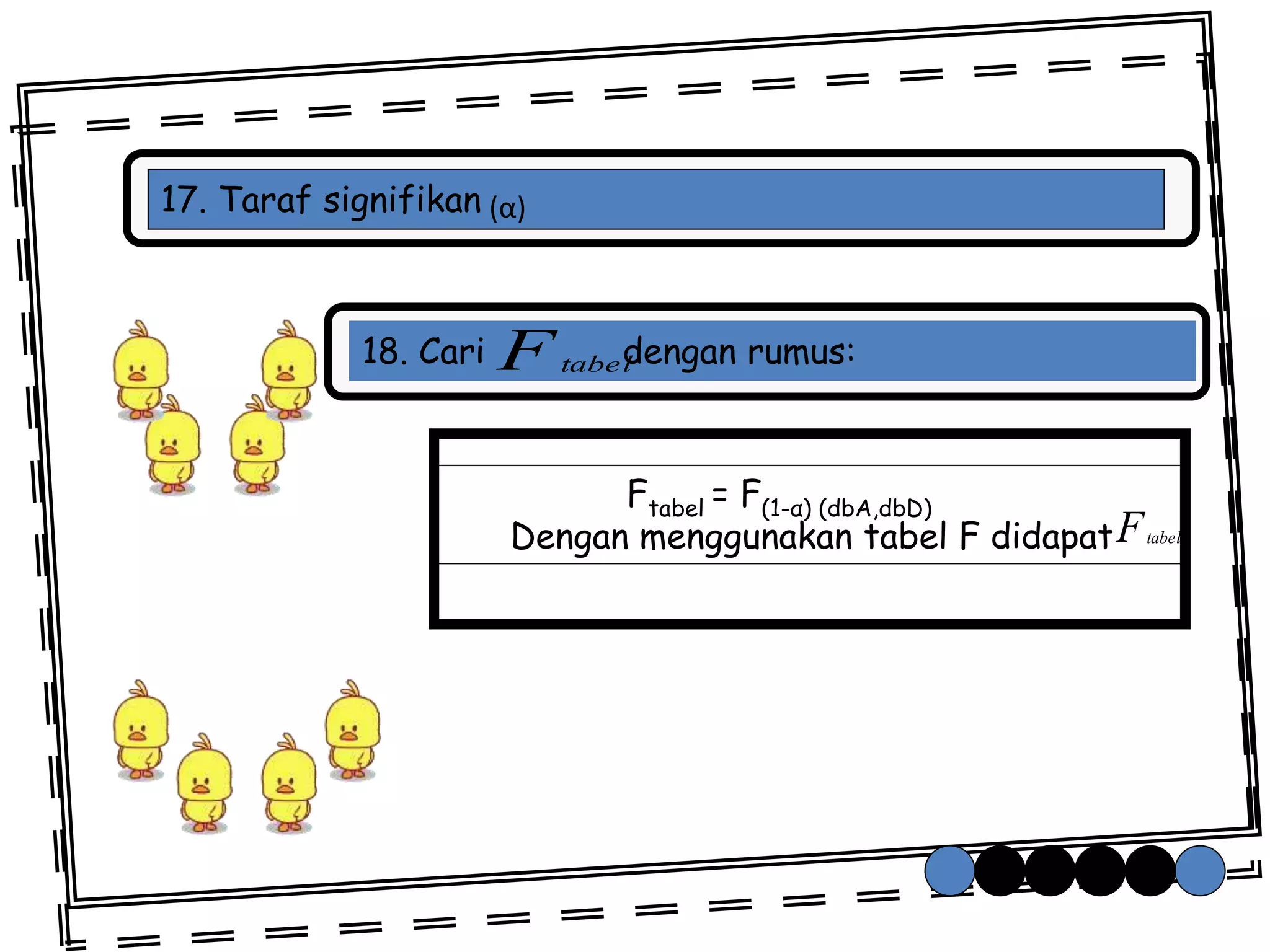
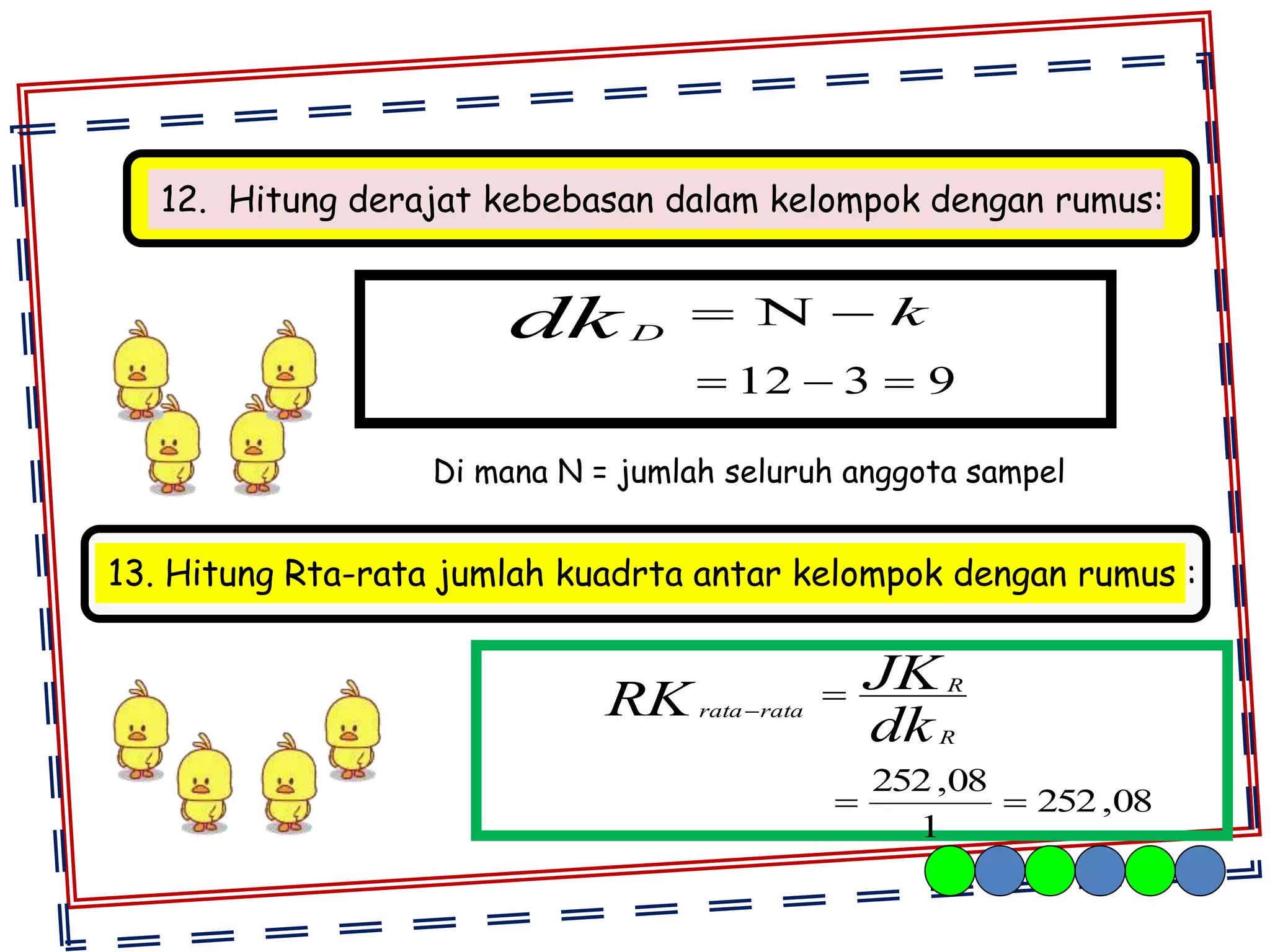
Analisis varian (ANAVA) digunakan untuk membandingkan rata-rata lebih dari dua kelompok data. Langkah-langkahnya meliputi membuat tabel penolong, menghitung jumlah kuadrat antar dan dalam kelompok, derajat kebebasan, dan nilai-F. Contoh soal menguji tiga prosedur kerja menggunakan ANAVA satu jalur dan menyimpulkan tidak ada perbedaan signifikan antara ketiganya.

1. NAMA
NAMA
NAMA

2. ANALYSIS OF VARIANCE
(ANAVA/ANOVA)
SATU JALUR
……………..

3. S
PENDAHULUAN
A. Latar Belakang
T A T SI T I K
P E N D I D I K A N
HOME
B. Rumusan Masalah
C. Tujuan Pembuatan makalah

4. A. PENGERTIAN ANAVA
Analisis varian (ANAVA) adalah
prosedur perhitungan yang mencoba
menganalisis varian dari responden atau
hasil perlakuan dari setiap kelompok data
dari veriabel independen. NEXT
PEMBAHASAN

5. B. Tujuan Anova satu jalur
Tujuan dari uji anova satu jalur adalah untuk membandingkan
lebih dari dua rata-rata. Sedangkan gunanya untuk menguji
kemampuan generalisasi. Maksudnya dari signifikansi hasil
penelitian Jika terbukti berbeda berarti kedua sampel tersebut
dapat digeneralisasikan (data sampel dianggap dapat mewakili populasi).
Anova satu jalur dapat melihat perbandingan
lebih dari dua kelompok data.

6. Langkah-langkah Anova satu jalur
1. Uji atau asumsikan bahwa data masing-masing dipilih
secara acak
2. Uji atau asumsikan bahwa data masing-masing
berdistribusi normal
3. Uji atau asumsikan bahwa data masing-masing
homogen
4. Tuliskan ( Ha dan H0) dalam bentuk kalimat
5. Tuliskan ( Ha dan H0) dalam bentuk statistik.
NEXT

7. 6. Buatlah tabel penolong anava sebagai berikut:
Tabel penolong anava
Nomor
Responden
VARIABEL BEBAS
Nn1 n2 n3
nn
x1
 x2
 x3
 xn
 
x1 x2 x3 xn
s
2
1s
2
2 s
2
3sn
2
1
2
......
 n
3

8. 7. Hitunglah jumlah kuadrat rata-rata dengan
rumus :
8. Hitung jumlah kuadrat antar kelompok dengan
rumus:
 
nnnn
xxxx
JK
n
n
R




......
......
321
2
321
     
JK
x
n
x
n
x
n
x
JK R
n
A

 )(
2
3
2
3
2
2
2
1
2
1
........
........

9. 10. Hitung derajat kebebasan rata-rata dengan rumus:
9. Hitung jumlah kuadrat dalam kelompok dengan rumus:
JKJKxJK A
R
D
  2
1dk ratarata
11. Hitung derajat kebebasan antar kelompok dengan rumus:
1 kdk A
Dimana k= banyak kelompok

10. 12. Hitung derajat kebebasan dalam kelompok dengan rumus:
kdkD

13. Hitung Rta-rata jumlah kuadrta antar kelompok dengan rumus :
Di mana N = jumlah seluruh anggota sampel
dk
JK
RK
R
R
ratarata


11. 15. Rata-rata jumlah kuadrat dalam kelompok dengan rumus:
14. Rata-rata jumlah kuadrat antara kelompok dengan rumus:
16. Cari dengan rumus:
dk
JK
RK
A
R
A

dk
JK
RK
D
D
D

Fhitung
RK
RKF
D
A
hitung


12. 17. Taraf signifikan
18. Cari dengan rumus:
(α)
Ftabel
Ftabel = F(1-α) (dbA,dbD)
Dengan menggunakan tabel F didapatFtabel

13. 19. MASUKKAN SEMUA NILAI YANG TELAH DIDAPAT KE
DALAM TABLE ANAVA BERIKUT:
TABEL ANOVA
NEXT
Jumlah
Variasi
Jumlah
Kuadrat
(JK)
dk Rata-rata
Kuadrat
(RK)
F
Rata-rata
Antar Klpk
Dalam Klpk
1
Jumlah
JKR
JKA
JKD
dkD
dkA
RKR
RK A
RKD
Fhitung
X 2
 n
1


14. 20. Tentukan kriteria pengujiannya yaitu:
diterimamak a HFJikaF tabelhitung 0,

21. Bandingkan FF tabelhitung
dengan
22. Buatlah kesimpulannya
H 0
23. Seandainya ternyata ditolak, maka perbandingan dilanjutkan agar
dapat diketahui pasangan mana yang berbeda dengan menggunakan uji t.
H0

15. Contoh soal:
Dari suatu pengamatan didapat data sebagai berikut:
TABEL PROSEDUR KERJA
NEXT
D. Contoh Soal dan Pembahasan
PROSEDUR YANG DICOBAKAN
A B C
Data Yang Dihasilkan 2
0
4
7
8
4
5
9
3
8
1
4
Pertanyaanya: Apakah ketiga prosedur kerja mereka berbeda:

16. NEXT
Ha H 0
1. Uji atau asumsikan bahwa data masing masing dipilih secara acak
2. Uji atau asumsikan bahwa data masing-masing berdistribusi normal.
3. Uji atau asumsikan bahwa data masing-masing homogeny.
4. Tulis dan dalam bentuk kalimat:
: Terdapat perbedaan yang signifikan antara A, B, dan C
: Tidak terdapat perbedaan yang signifikan antara A, B, dan C
H a
H 0
JAWAB ……..

17. NEXT
5. Hipotesis statistiknya.
: salah satu ada yang ≠
:  CBA

H0
Ha
n1
42
n 43
n 12N 131
x 262
 x 163
x 55 x
x 43
Prosedur yang akan dicoba
A B C
Data yang
dihasilkan
2 8 3
0 4 8
4 5 1
7 9 4
41
n 42
n 43
n 12N
131
x 262
 x
163
x 55 x
25,31
x 5,6
2
x x 43
92,8
2
1
s 67,5
2
2
s 67,8
2
3
s
6. Buatlah tabel penolong Anava sebagai berikut:

18. 7. Hitunglah jumlah kuadrat rata-rata dengan rumus :
8. Hitung jumlah kuadrat antar kelompok dengan
rumus:
 
nnnn
xxxx
JK
n
n
R




......
......
321
2
321
     
JK
x
n
x
n
x
n
x
JK R
n
A

 )(
2
3
2
3
2
2
2
1
2
1
........
........
08,252
444
)162613( 2




     
17,23
08,252
162613
444
222



19. 10. Hitung derajat kebebasan rata-rata dengan rumus:
9. Hitung jumlah kuadrat dalam kelompok dengan rumus:
JKJKxJK A
R
D
  2
1dk ratarata
11. Hitung derajat kebebasan antar kelompok dengan rumus:
1 kdk A
Dimana k= banyak kelompok
75,69
17,2308,252345


213 

20. 12. Hitung derajat kebebasan dalam kelompok dengan rumus:
kdk D

13. Hitung Rta-rata jumlah kuadrta antar kelompok dengan rumus :
Di mana N = jumlah seluruh anggota sampel
dk
JK
RK
R
R
ratarata

9312 
08,252
1
08,252


21. 15. Rata-rata jumlah kuadrat dalam kelompok dengan rumus:
14. Rata-rata jumlah kuadrat antara kelompok dengan rumus:
16. Cari dengan rumus:
dk
JK
RK
A
R
A

dk
JK
RK
D
D
D

Fhitung
RK
RKF
D
A
hitung

58,11
2
17,23

75,7
9
75,69

49,1
75,7
58,11


22. 17. Taraf signifikan
18. Cari dengan rumus:
(α) = 0,05.
Ftabel
Ftabel = F(1-α) (dbA,dbD)
=F(1-0,05) (2,9)
Dengan menggunakan tabel F didapatFtabel

23. 19. MASUKKAN SEMUA NILAI YANG TELAH DIDAPAT KE
DALAM TABLE ANAVA BERIKUT:
TABEL ANOVA
NEXT
Jumlah
Variasi
Jumlah
Kuadrat
(JK)
dk Rata-rata
Kuadrat
(RK)
F
Rata-rata
Antar Klpk
Dalam Klpk
252,08
23,17
69,75
1
2
9
252,08
11,58
7,75
1,49
Jumlah 345 12 - -

24. 20. Kriteria pengujiannya yaitu:
: Tidak signifikan
Jika
SignifikanH :0
21. Ternyata diterimasehingga26,449,1 
22. kesimpulannya
Yang berbunyi: “tidak terdapat perbedaan yang
signifikan antara A, B, dan C, diterima. Sebaliknya yang berbunyi:
” terdapat perbedaan yang antara A, B, dan C” ditolak.
H 0
H a
diterimamakaHFF tabelhitung 0
,
H 0
H0
Ha

25. KESIMPULAN
Anava atau Anova adalah sinonim dari analisis varians terjemahan
dari analysis of variance, sehingga banyak orang menyebut dengan
anova. Analisis anova banyak digunakan pada penelitian-penelitian
yang banyak melibatkan pengujian komparatif ,yaitu menguji variabel
terikat dengan cara membandingkan pada kelompok-kelompok sampel
independen yang diamati
PENUTUP