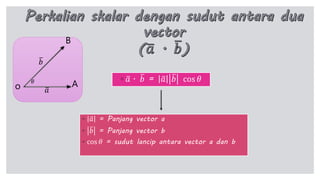
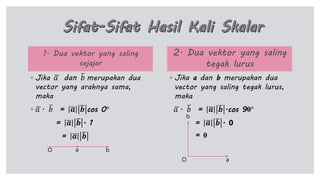
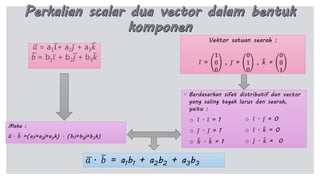
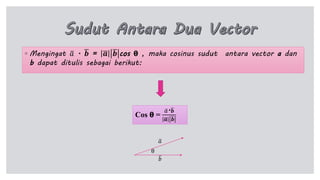
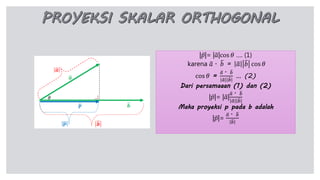
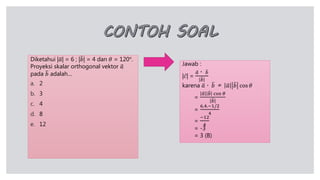
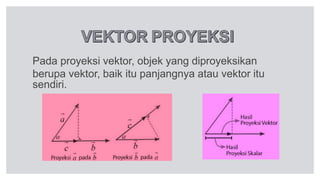
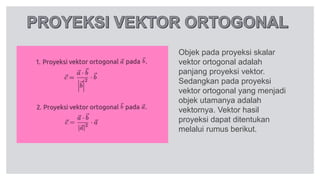
Dokumen tersebut membahas tentang perkalian skalar dua vektor, termasuk rumus dan sifat-sifatnya. Rumus utama perkalian skalar dua vektor adalah a.b = a b cos θ, di mana a dan b adalah panjang vektor, dan θ adalah sudut antara kedua vektor. Dibahas pula konsep proyeksi vektor ortogonal dan rumus untuk menentukan panjang proyeksi.

1. PERKALIANSKALARDUA
VEKTOR
Nada Wahyudia (27) Sandra Fatimah (33)
Athifah Radhiyah H.(5) Helga Syahda E. (17)

2. ◦ 𝑎 . 𝑏 = 𝑎 𝑏 cos 𝜃
◦ 𝑎 = Panjang vector a
◦ 𝑏 = Panjang vector b
◦ cos 𝜃 = sudut lancip antara vector a dan b
𝜃
o
B
A
𝑏
𝑎

3. 1) Tentukan hasil kali scalar vector a dan b pada gambar di bawah, jika 𝒂 = 8 dan 𝒃 = 5, dan
besar sudut antara vector a dan b adalah 60°.
Jawab : 𝑎 . 𝑏 =
𝒂 𝒃 cos θ
𝑎 . 𝑏 = 8.5 cos 60°
= 40 . 0,5
= 20
60°
𝑎
𝑏

4. 1. Dua vektor yang saling
sejajar
◦ Jika 𝑎 dan 𝑏 merupakan dua
vector yang arahnya sama,
maka
◦ 𝑎 . 𝑏 = 𝒂 𝒃 cos 0°
= 𝒂 𝒃 . 1
= 𝒂 𝒃
2. Dua vektor yang saling
tegak lurus
◦ Jika a dan b merupakan dua
vector yang saling tegak lurus,
maka
𝑎 . 𝑏 = 𝒂 𝒃 .cos 90°
= 𝒂 𝒃 . 0
= 0
a bO
aO
b

5. 3. Dua vektor yang
berlawanan arah
◦ Jika a dan b merupakan dua
vector yang arahnya
berlawanan, maka
a . b = 𝒂 𝒃 cos 180°
= 𝒂 𝒃 -1
= - 𝒂 𝒃
4. Tanda hasil kali skalar
dua vektor
◦ Tanda dari hasil kali scalar dua
vector ditentukan oleh besar
sudut yang dibentuk oleh dua
vector tersebut.
ab O
BESAR SUDUT
(Ø)
TANDA
0 _< Ø < 90° POSITIF
Ø = 90° NOL
90° < Ø <_ 180° NEGATIF

6. 5. Sifat komutatif
𝑎 . 𝑏 = 𝑏 . 𝑎
𝑎 . 𝑏 = 𝒂 𝒃 cos Ø , dan
𝑏 . 𝑎 = 𝒃 𝒂 cos Ø
Oleh karena 𝒂 𝒃 = 𝒃 𝒂
Maka 𝑎 . 𝑏 = 𝑏 . 𝑎
6. Sifat distributif
𝒂 . ( 𝒃 + 𝒄) = 𝑎 . 𝑏 + 𝑎 . 𝑐

7. 𝑎 = a1 𝑖+ a2 𝑗 + a3 𝑘
𝑏 = b1 𝑖 + b2 𝑗 + b3 𝑘
Maka :
𝑎 . 𝑏 =(a1i+a2j+a3k) . (b1i+b2j+b3k)
Vektor satuan searah :
𝑖 =
1
0
0
, 𝑗 =
0
1
0
, 𝑘 =
0
0
1
◦ Berdasarkan sifat distributif dan vector
yang saling tegak lurus dan searah,
yaitu :
o 𝑖 . 𝑗 = 0
o 𝑖 . 𝑘 = 0
o 𝑗 . 𝑘 = 0
o 𝑖 . 𝑖 = 1
o 𝑗 . 𝑗 = 1
o 𝑘 . 𝑘 = 1
𝑎 . 𝑏 = a1b1 + a2b2 + a3b3

8. Diberikan vector-vector 𝑎 =
5
4
6
dan 𝑏 =
2
3
1
. Tentukan : a) 𝑎 . 𝑏 b) 𝑎 . 𝑎 c) 𝑏 . 𝑏
Jawab :
a) 𝑎 . 𝑏 =
5
4
6
.
2
3
1
= (5 . 2) + (4 . 3) + (6 . 1)
= 10 + 12 + 6
= 28
b) 𝑎 . 𝑎 =
5
4
6
.
5
4
6
= (5 . 5) + (4 .4) + (6 .6)
= 25 + 16 + 36
= 77
c) 𝑏 . 𝑏 =
2
3
1
.
2
3
1
= (2 . 2) + (3 . 3) + (1 . 1)
= 4 + 9 + 1
= 14

9. ◦ Mengingat 𝑎 . 𝒃 = 𝒂 𝒃 cos 𝛉 , maka cosinus sudut antara vector a dan
b dapat ditulis sebagai berikut:
Cos 𝛉 =
𝑎. 𝒃
𝒂 𝒃
θ
𝑎
𝑏

10. Diketahui vector a = 2i + 5j + 4k dan b = I + 2j – 3k. Sudut
antara A dan B adalah…
Pembahasan :
Berdasarkan rumus perkalian scalar,
a.b = 𝒂 𝒃 cos Ø
(2i+5j+4k)(i+2j–3k) = 𝒂 𝒃 cos Ø
2 + 10 – 12 = 𝒂 𝒃 cos Ø
0 = 𝒂 𝒃 cos Ø
cos Ø = 0
Ø = 90°

11. Jika vector a = 4 𝑖 – 2 𝑗 – 6 𝑘 dan vector b = -5 𝑖 + m 𝑗 – 4 𝑘 saling
tegak lurus, maka nilai m adalah …
Pembahasan :
𝑎 . 𝑏 = 𝒂 𝒃 cos Ø
𝑎 . 𝑏 = 𝒂 𝒃 cos 90
(4 𝑖-2 𝑗-6 𝑘)(-5 𝑖+m 𝑗–4 𝑘) = 0
-20 – 2m + 24 = 0
-2m + 4 = 0
-2m = -4
m = 2

12. Diketahui vektor u = i + 4 𝑗 + 5 𝑘 dan vector v = -i + 4 𝑗 + 5 𝑘. Sudut
yang dibentuk oleh oleh kedua vector tersebut adalah …
Pembahasan :
𝑢 . 𝑣 = 𝒖 𝒗 cos Ø
( 𝑖+ 4 𝑗 + 5 𝑘).(- 𝑖+ 4 𝑗 + 5 𝑘)= 𝒖 𝒗 cos Ø
-1+4+5 = 12 + 4
2
+ 5
2
. −12 + 4
2
+ 5
2
cos Ø
8 = 10 . 10 cos Ø
8 = 10 cos Ø
8
10
= cos Ø
Ø = 37 derajat

13. Vektor Proyeksi

14. | 𝑝|= | 𝑎|cos 𝜃 …. (1)
karena 𝑎 . 𝑏 = 𝑎 𝑏 cos 𝜃
cos 𝜃 =
𝑎 . 𝑏
𝑎 𝑏
… (2)
Dari persamaaan (1) dan (2)
| 𝑝|= | 𝑎|
𝑎 . 𝑏
𝑎 𝑏
Maka proyeksi p pada b adalah
| 𝑝|=
𝑎 . 𝑏
𝑏

15. Diketahui | 𝑎| = 6 ; | 𝑏| = 4 dan 𝜃 = 120°.
Proyeksi skalar orthogonal vektor 𝑎
pada 𝑏 adalah…
a. 2
b. 3
c. 4
d. 8
e. 12
Jawab :
| 𝑐| =
𝑎 . 𝑏
𝑏
karena 𝑎 . 𝑏 = 𝑎 𝑏 cos 𝜃
=
𝑎 𝑏 cos 𝜃
𝑏
=
6.4.−1/2
4
=
−12
4
= -3
= 3 (B)

16. Pada proyeksi vektor, objek yang diproyeksikan
berupa vektor, baik itu panjangnya atau vektor itu
sendiri.

17. Objek pada proyeksi skalar
vektor ortogonal adalah
panjang proyeksi vektor.
Sedangkan pada proyeksi
vektor ortogonal yang menjadi
objek utamanya adalah
vektornya. Vektor hasil
proyeksi dapat ditentukan
melalui rumus berikut.

18. ◦ Panjang proyeksi ortogonal vektor pada adalah 4. Nilai p adalah ….

19. THANKYOU