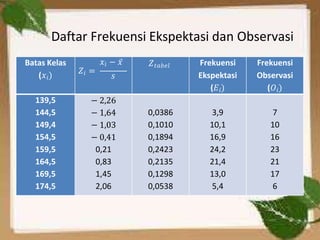
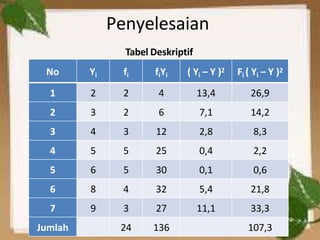
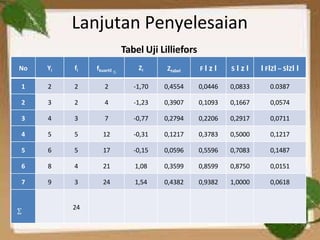
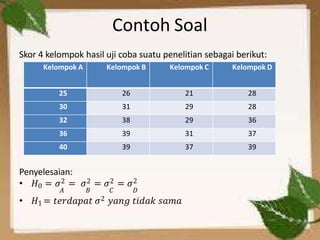
Dokumen tersebut membahas tentang uji normalitas dan homogenitas data. Secara singkat, dibahas tentang beberapa metode uji normalitas seperti uji Chi-Kuadrat dan uji Liliefors beserta contoh soalnya. Juga dibahas tentang uji homogenitas menggunakan uji Hartley beserta contoh penyelesaiannya.

1. UJI Normalitas dan
Homogenitas
Ronal rahmad sihombing
Pjkr E 20
6203311042

2. Uji Normalitas
Cara menentukan data distribusi normal
atau tidak diantaranya:
1. Grafik Ogive
2. Tingkat kemiringan
3. Uji Chi-Kuadrat
4. Uji Liliefor
5. Uji Kolmogorov-Smirnov
Dll
Statistik
Deskriptif
Statistik
Induktif

3. Uji Chi-Kuadrat
Hipotesis:
𝐻0:Tidak ada perbedaan distribusi frekuensi populasi
𝐻1: Ada perbedaan distribusi frekuensi populasi
Pengujian:
𝑖
=1
𝑘
𝑂 − 𝐸
𝛘2 = ∑ 𝑖 𝑖
2
𝐸𝑖
Dimana:
𝑂𝑖=frekuensi observasi/pengamatan ke-i,
𝐸𝑖= frekuensi harapan ke i
k = jumlah kelas/kelompok
𝐻0 ditolak jika 𝛘2 > 𝛘2 dengan derajat bebas(db)
ℎ𝑖𝑡. 𝛼
Untuk Data Tunggal
𝑑𝑏 = 𝑘 − 1
Untuk Data Kelompok
𝑑𝑏 = 𝑘 − 3

4. Contoh Soal
Ujikan normal atau tidak data pengukuran
terhadap tinggi mahasiswa tingkat pertama
dilakukan dan diambil sebuah sampel acak
berukuran 100 berikut dengan metode chi-
square? Tinggi (cm) f
140 – 144 7
145 – 149 10
150 – 154 16
155 – 159 23
160 – 164 21
165 – 169 17
170 – 174 6
Jumlah 100

5. Penyelesaian:
Setelah dihitung 𝑥̅ = 157,8 dan 𝑆 = 8,09.
Selanjutnya tentukan batas-batas kelas dan cari
𝑖
nilai 𝑍 =
𝑥𝑖−𝑥
𝑠 𝑡𝑎𝑏𝑒
𝑙
̅
kemudian lihat 𝑍 . Dari
𝑍𝑡𝑎𝑏𝑒𝑙 pada tepi atas dan bawah didapat
peluang kelas ke-i dan frekuensi ekspektasinya
dihitung dengan cara mengalikan peluang kelas
dengan jumlah frekuensi.

6. Daftar Frekuensi Ekspektasi dan Observasi
Batas Kelas
(𝑥𝑖)
𝑥𝑖 − 𝑥̅
𝑍𝑖 =
𝑠
𝑍𝑡𝑎𝑏𝑒𝑙 Frekuensi
Ekspektasi
(𝐸𝑖)
Frekuensi
Observasi
(𝑂𝑖)
139,5 − 2,26
144,5 − 1,64 0,0386 3,9 7
149,4 − 1,03 0,1010 10,1 10
154,5 − 0,41 0,1894 16,9 16
159,5 0,21 0,2423 24,2 23
164,5 0,83 0,2135 21,4 21
169,5 1,45 0,1298 13,0 17
174,5 2,06 0,0538 5,4 6

7. 𝜒2
=
(7 − 3,9)2
3,9
+
(10 − 10,1)2
10,1
+
(16 − 18,9)2
+
(23 − 24,2)2
+
(21 − 21,4)2
21,4
+
18,9
(17 − 13,0)2
13,0
+
24,2
(6 − 5,5)2
5,4
= 4,27
Dari daftar frekuensi dapat dilihat 𝑘 = 7 jadi 𝑑𝑏 = 4,
misal gunakan signifikansi 𝛼 = 0,05 :
ℎ𝑖𝑡
.
𝛼 𝛼
𝜒2 = 9,49 berarti 4,27 < 9,49  𝜒2 < 𝜒2
sehingga 𝐻0 diterima berarti daftartersebut berdistribusi
normal

8. Uji Liliefor
Untuk melakukan uji normalitas dengan cara ini
maka:
• Menentukan taraf signifikansi (𝛼) yaitu misalkan
pada 𝛼 = 5% (0,05) dengan hipotesis yang akan
diuji:
𝐻0 = Data berdistribusi normal, melawan
𝐻1= Data tidak berdistribusi normal
Dengan kriteria pengujian:
Jika 𝐿𝑂
Jika 𝐿𝑂
= 𝐿ℎ𝑖𝑡𝑢𝑛𝑔
= 𝐿ℎ𝑖𝑡𝑢𝑛𝑔
< 𝐿𝑡𝑎𝑏𝑒𝑙 terima 𝐻0
> 𝐿𝑡𝑎𝑏𝑒𝑙 tolak 𝐻0

9. Lanjutan Uji Liliefors
• Lakukan langkah-langkah pengujian normalitas berikut;
(1) Data pengamatan 𝑌1, 𝑌2, 𝑌3, ... , 𝑌𝑛 dijadikan bilangan
baku 𝑍1, 𝑍2, 𝑍3, ... , 𝑍𝑛 dengan menggunakan rumus :
𝑍𝑖 =
(𝑌𝑖 − 𝑌̅)
𝑠
(2) Untuk setiap bilangan baku ini dengan menggunakan
daftar distribusi normal baku, kemudian dihitung peluang
𝐹 𝑍𝑖 = 𝑃(𝑍 ≤ 𝑍𝑖)

10. Lanjutan Uji Liliefors
(3) Hitung proporsi 𝑍1, 𝑍2, 𝑍3, ... , 𝑍𝑛 yang lebi kecil atau sama
dengan Z. Jika proporsi ini dinyatakan dengan S(𝑍𝑖) maka:
𝑆 𝑍𝑖 =
𝑓𝑟𝑒𝑘𝑢𝑒𝑛𝑠𝑖 𝐾𝑢𝑚𝑢𝑙𝑎𝑡𝑖𝑓
𝑛
(4) Hitung 𝐹 𝑍𝑖 − 𝑆(𝑍𝑖) dan tentukan harga mutlaknya
(5) Harga mutlak yang paling besar sebagai harga 𝐿𝑂 atau
𝐿ℎ𝑖𝑡𝑢𝑛𝑔
• Untuk menerima atau menolak hipotesis nol (𝐻0),
bandingkan 𝐿𝑂 dengan 𝐿𝑡𝑎𝑏𝑒𝑙 yang didapat dari tabel
liliefors untuk taraf nyata(signifikansi) yang dipilih.

11. Contoh Soal
Lakukan uji normalitas dari hasil pengumpulan
data suatu sampel berikut :
2 3 4 2 4 3 5 4
5 5 6 6 6 5 5 9
6 6 8 8 8 8 9 9

12. Penyelesaian
Tabel Deskriptif
No Yi fi fiYi ( Yi – Y )2 Fi ( Yi – Y )2
1 2 2 4 13,4 26,9
2 3 2 6 7,1 14,2
3 4 3 12 2,8 8,3
4 5 5 25 0,4 2,2
5 6 5 30 0,1 0,6
6 8 4 32 5,4 21,8
7 9 3 27 11,1 33,3
Jumlah 24 136 107,3

13. Lanjutan Penyelesaian
• Sehingga didapat, mean =𝑌̅ = ∑ 𝑓i –
Yi = 5,7
∑ 𝑓i
• simpangan baku = s =
∑ 𝑓𝑖(𝑌𝑖 −𝑌)2
= 2,2
• Selanjutnya,
𝑛−1
konversi setiap
lakukan
mentah Yi menjadi nilai baku Zi,
nilai
dan
selanjutnya tentukan nilai LO

14. Lanjutan Penyelesaian
Tabel Uji Lilliefors
No Yi fi fkuartil ≤
Zi Ztabel F I z I S I z I I FIZI – SIZI I
1 2 2 2 -1,70 0,4554 0,0446 0,0833 0.0387
2 3 2 4 -1,23 0,3907 0,1093 0,1667 0,0574
3 4 3 7 -0,77 0,2794 0,2206 0,2917 0,0711
4 5 5 12 -0,31 0,1217 0,3783 0,5000 0,1217
5 6 5 17 -0,15 0,0596 0,5596 0,7083 0,1487
6 8 4 21 1,08 0,3599 0,8599 0,8750 0,0151
7 9 3 24 1,54 0,4382 0,9382 1,0000 0,0618
∑
24

15. Lanjutan Penyelesaian
Dari hasil perhitungan dalam tabel tersebut
didapat LO = 0,1487; sedangkan dari tabel
Lilliefors untuk dan n=24 didapat nilai Llabel =
0,173. Karena nilai LO < L maka H0 diterima
disimpulkan “ data atau sampel berdistribusi
normal”.

16. Uji Homogenitas
Homogen  syarat uji statistik inferensial
parametrik
Terknik Pengujiannya antara lain:
1. Uji Hartley
2. Uji Bartlett
Dll

17. Uji Hartley
𝐹 𝑚𝑎𝑥 =
𝑉𝑎𝑟𝑖𝑎𝑛𝑠𝑖 𝑡𝑒𝑟𝑏𝑒𝑠𝑎𝑟
𝑉𝑎𝑟𝑖𝑎𝑛𝑠𝑖 𝑡𝑒𝑟𝑏𝑒𝑠𝑎𝑟
Adapun kriteria pengujiannya sebagai berikut:
• Terima 𝐻0 jika 𝐹(max )ℎ𝑖𝑡𝑢𝑛𝑔 ≤ 𝐹(max )𝑡𝑎𝑏𝑒𝑙
• Tolak 𝐻0 jika 𝐹(max )ℎ𝑖𝑡𝑢𝑛𝑔 > 𝐹(max )𝑡𝑎𝑏𝑒𝑙
• 𝐻0 menyatakan variansi homogen sedangkan 𝐻1
menyatakan variansi tidak homogen

18. Contoh Soal
Skor 4 kelompok hasil uji coba suatu penelitian sebagai berikut:
Penyelesaian:
• 𝐻0 = 𝜎2 = 𝜎2 = 𝜎2 = 𝜎2
𝐴 𝐵 𝐶 𝐷
• 𝐻1 = 𝑡𝑒𝑟𝑑𝑎𝑝𝑎𝑡 𝜎2 𝑦𝑎𝑛𝑔 𝑡𝑖𝑑𝑎𝑘 𝑠𝑎𝑚𝑎
Kelompok A Kelompok B Kelompok C Kelompok D
25 26 21 28
30 31 29 28
32 38 29 36
36 39 31 37
40 39 37 39

19. Lanjutan Penyelesaian:
Berdasarkan data diatas, hitung variansi masing-masing
kelompok:
𝐴 𝐶
𝑆2 = 32,8 𝑆2 = 32,8
𝐵
𝑆2 = 34,3 𝐷
𝑆2 = 27,3
34,3
𝐹(max )ℎ𝑖𝑡𝑢𝑛𝑔 =
27,3
= 1,2564
𝐹(max )𝑡𝑎𝑏𝑒𝑙 = 20,6 (𝑛 − 1 = 4, 𝑘 = 4)
Kesimpulan: 𝐻0 diterima katena 𝐹(max )ℎ𝑖𝑡𝑢𝑛𝑔 <
𝐹(max )𝑡𝑎𝑏𝑒𝑙 yang berarti keempat kelompok itu homogen