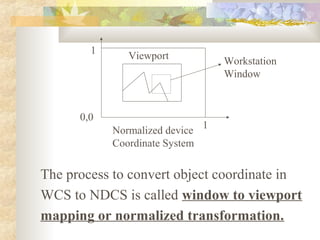
Here are the steps to solve this question: (a) Given: Window: wxmin = 2, wymin = 2 wxmax = 3, wymax = 4 Viewport: vxmin = 0, vymin = 0 vxmax = 1, vymax = 1 Sx = 1 - 0 = 1/1 = 1 3 - 2 = 1 Sy = 1 - 0 = 1/2 = 1/2 4 - 2 = 2 N = 1 0 0 0 1 0 0 0 1 (b) Given: Window: wxmin = 2, wymin = 2 wxmax = 3, wymax = 4 Viewport

1. It is a formal mechanism for displaying views
of a picture on an output device. A graphics
package allows the user to specify
a) Which part of the defined picture is to be
displayed.
b) Where the part is to be placed on the
display device.
Much like what we see in real life through a
small window or the view finder of a camera.

2. Objects are placed into the scene by modeling
transformation to a master coordinate
system, referred to as world coordinate
system (WCS).
A WCS area selected for display is called
window. The window defines what is to be
viewed. Window is a rectangle finite
region whose edges are parallel to the
WCS.
Sometimes an additional coordinate system
called a viewing coordinate system is
introduced to show the effect of moving view.

3. Window
World Coordinate System
An image representing a view often becomes
part of a larger image, like a photo on an
album page. Since album pages vary &
monitor size differs from one system to
another, so we want to introduce a device

4. independent tool to describe the display area,
called normalized device coordinate system
(NDCS) in which virtual display device’s area
is (1 x 1)square & lower left corner is at
origin
(0,0) of the coordinate system.
The area on a display device to which a
window is mapped is called a viewport.
The viewport defines where the view is to
be displayed. The rectangle viewport with
its edges parallel to the axes of the NDCS

5. 1 Viewport Workstation
Window
0,0
Normalized device 1
Coordinate System
The process to convert object coordinate in
WCS to NDCS is called window to viewport
mapping or normalized transformation.

6. The process that maps NDCS to discrete
device/image coordinate is called
workstation transformation.
Workstation
Viewport
Device/Image co-ordinate System

7. Which is a 2nd window to viewport mapping
with a workstation window in NDCS &
workstation viewport in device coordinate
system. These two coordinate mapping
Opn. refers to as viewing transformation.

8. Window to Viewport Transformation
Once object description have been transferred
to the viewing reference frame, we choose
the window extents in viewing coordinate
& select the viewport limit in normalized
coordinates. Object description are then
transferred to normalized device coordinate
This can be done by using the transformation
that maintain the same relative placement
of object in normalized space as they had
in viewing coordinates.

9. For eg.- if a coordinate position is at center of
the viewing window, it will be displayed at
the center of the viewport.
(xw,yw) (xv,yv)
ywmax
yvmax
ywmin yvmin
xwmin xwmax xvmin xvmax
WCS NDCS

10. The objective of window to viewport mapping
is to convert the world coordinate (wx,wy)
of an arbitrary point to its corresponding
normalized device coordinate (vx,vy). In
order to maintain the same relative
placement of point in the viewport as in the
window, we require
wx – wxmin = vx – vxmin --(1)
wxmax – wxmin vxmax - vxmin

11. wy – wymin = vy – vymin --(2)
wymax – wymin vymax – vymin
Solving these expressions for the viewport
position vx & vy we have
vx = vxmax – vxmin (wx – wxmin) + vx min
wxmax – wxmin
vx = Sx (wx – wxmin) + vx min
Sx = vxmax – vxmin
wxmax – wxmin

12. From (2)
vy = vymax – vymin (wy – wymin) + vy min
wymax – wymin
vy = Sy (wy – wymin) + vy min
Sy = vymax – vymin
wymax – wymin
Since the eight coordinate values that define
the window & the viewport are just constant,
we can express these two formulas for
computing (vx,vy) from (wx,wy) in terms of
translate-scale-translate transformation N.

13. vx wx
vy = N . wy
1 1
Where
N = 1 0 vxmin sx 0 0 1 0 -wxmin
0 1 vymin 0 sy 0 0 1 -wymin
0 0 1 0 0 1 0 0 1
Put the value of sx & sy.

14. Ques-1 Find the normalization transformation
that maps a window whose lower left
corner is at (1,1) & upper right corner is at
(3,5) onto
(i) Viewport that is entire normalized device
screen.
(ii) A viewport that has lower left corner at
(0,0) & upper right corner at (1/2,1/2).
Solution: (i) wxmin = 1 wymin = 1
wxmax = 3 wymax = 5

15. vxmin = 0 vymin = 0
vxmax = 1 vymax = 1
Sx = vxmax – vxmin = 1 – 0 =1
wxmax – wxmin 3 - 1 2
Sy = vymax – vymin = 1 - 0 = 1
wymax – wymin 5 - 1 4
N= 1 0 0 ½ 0 0 1 0 -1
0 1 0 0 ¼ 0 0 1 -1
0 0 1 0 0 1 0 0 1

16. = ½ 0 -1/2
0 ¼ -1/4
0 0 1
(ii) wxmin = 1 wymin = 1
wxmax = 3 wymax = 5
vxmin = 0 vymin = 0
vxmax = 1/2 vymax = 1/2
Sx = ½ - 0 = ½ = ¼
3- 1 2

17. Sy = ½ -0 = ½ = 1/8
5 -1 4
N = 1 0 0 1/4 0 0 1 0 -1
0 1 0 0 1/8 0 0 1 -1
0 0 1 0 0 1 0 0 1
¼ 0 -1/4
= 0 1/8 -1/8
0 0 1

18. Ques-2 Find the normalized transformation
that maps a window whose lower left
corner is at (2,2) & upper right corner is at
(3,4) onto
(a) A viewport that is the entire normalized
device screen and
(b) A viewport that has lowerleft corner at
(0,0) and upper left corner (3/2,3/2).