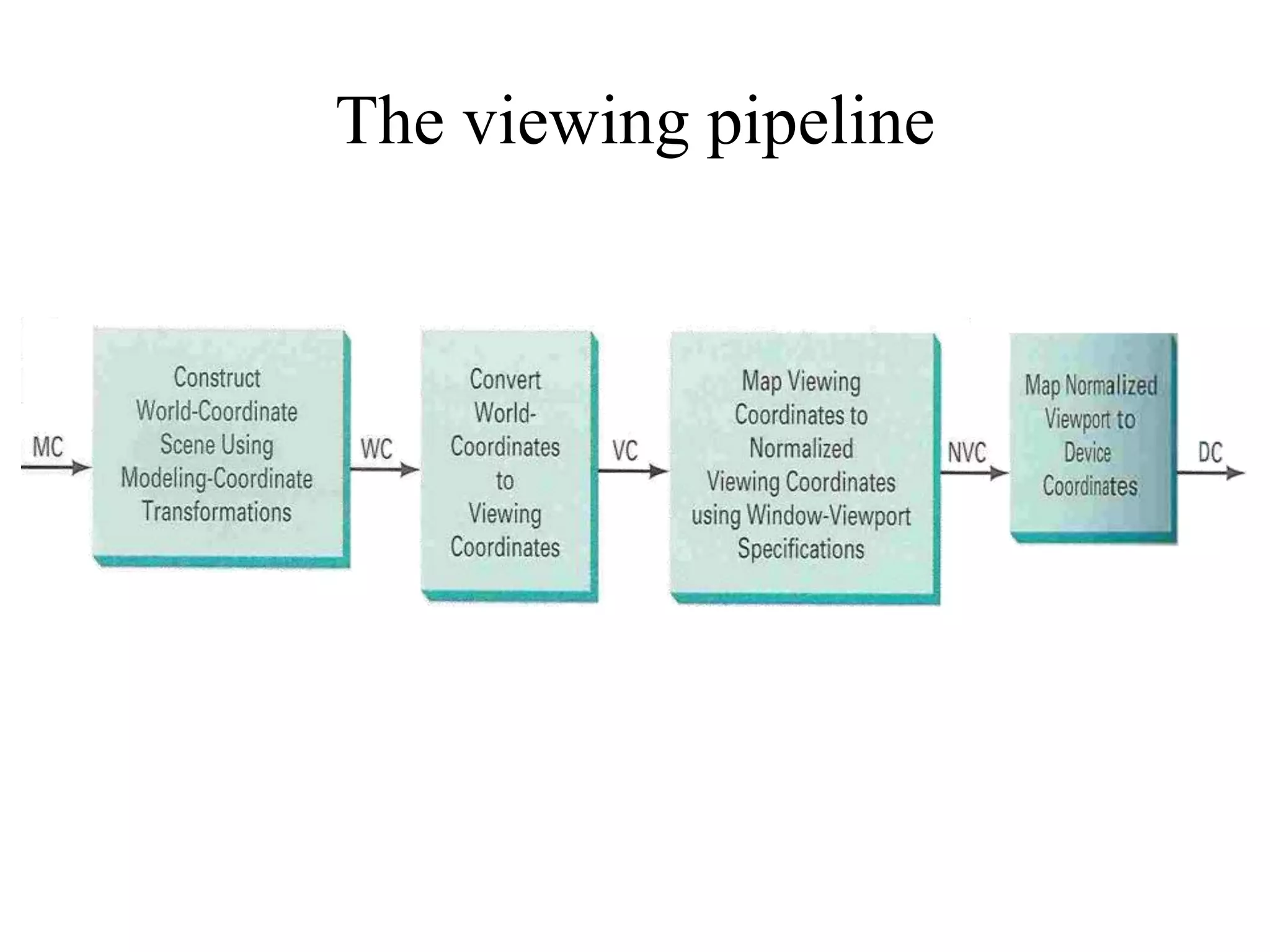
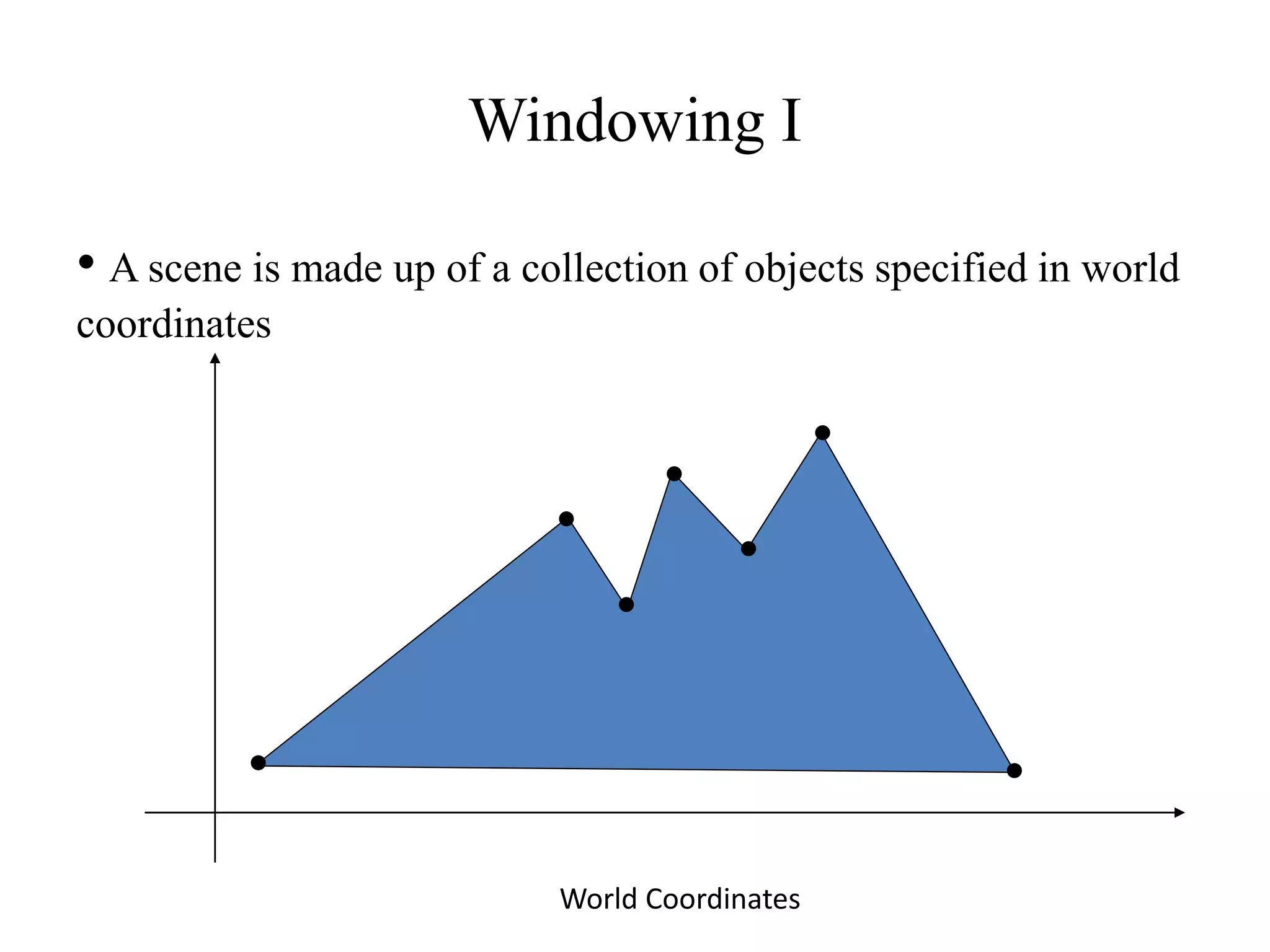
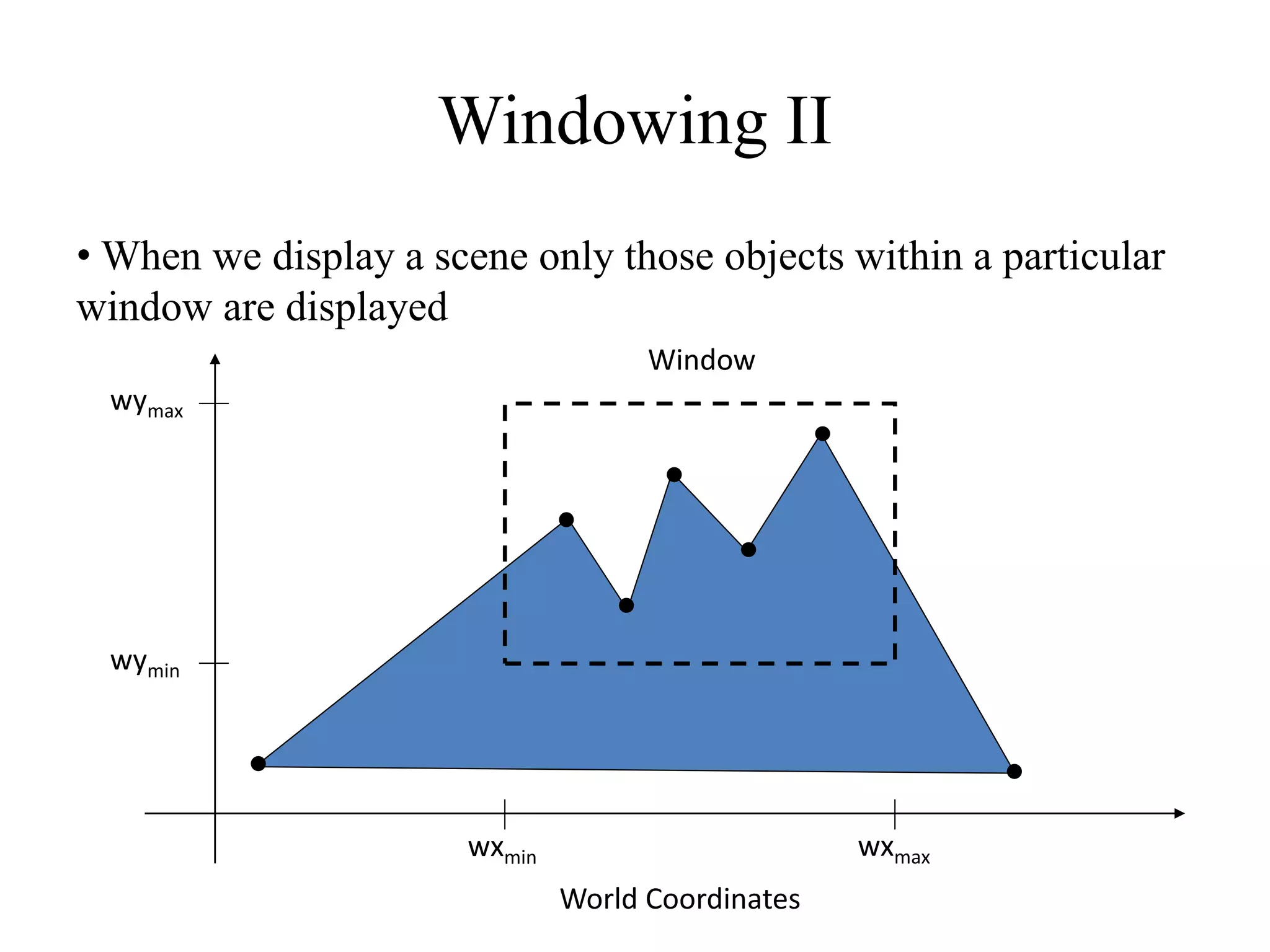
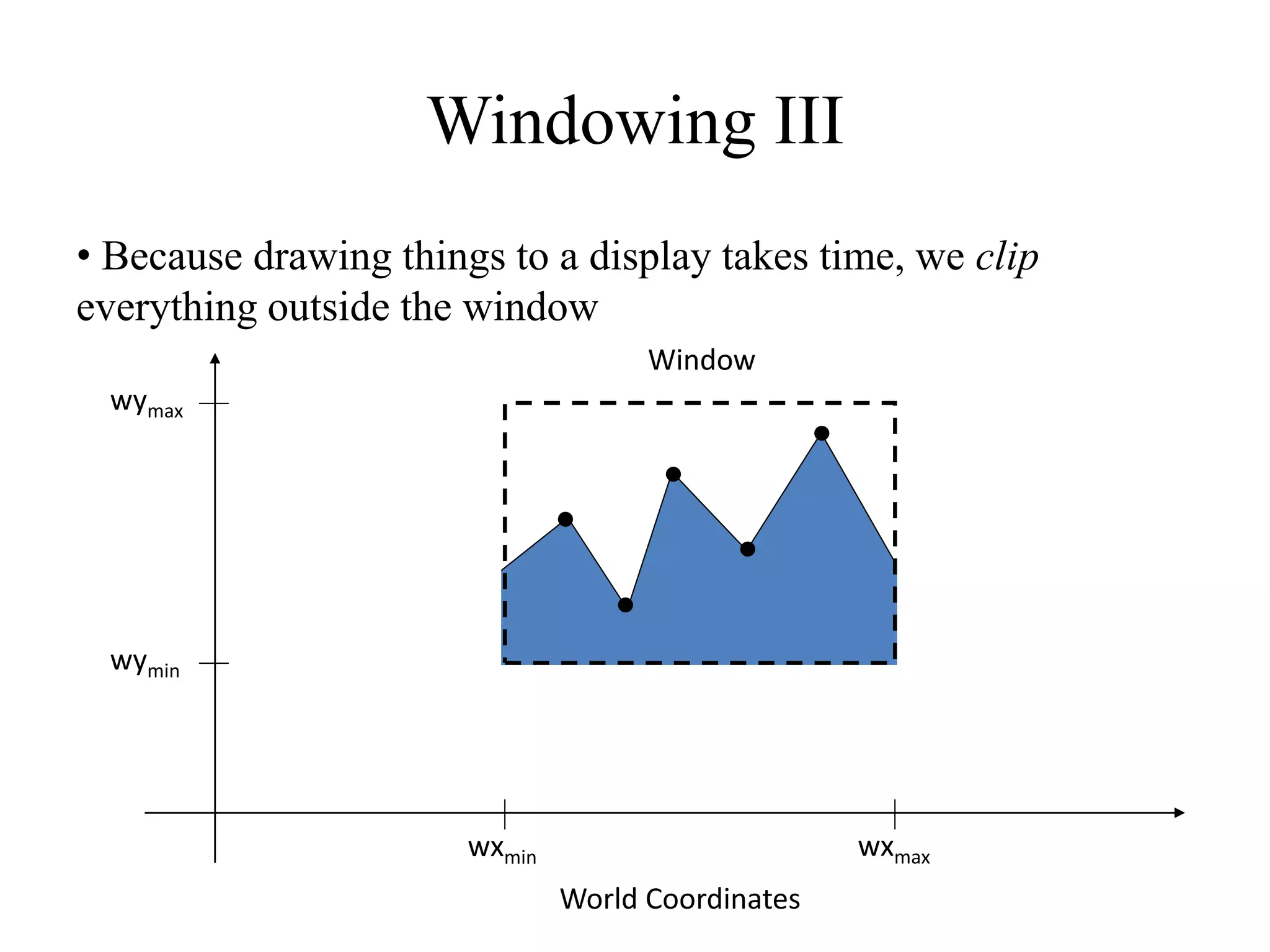
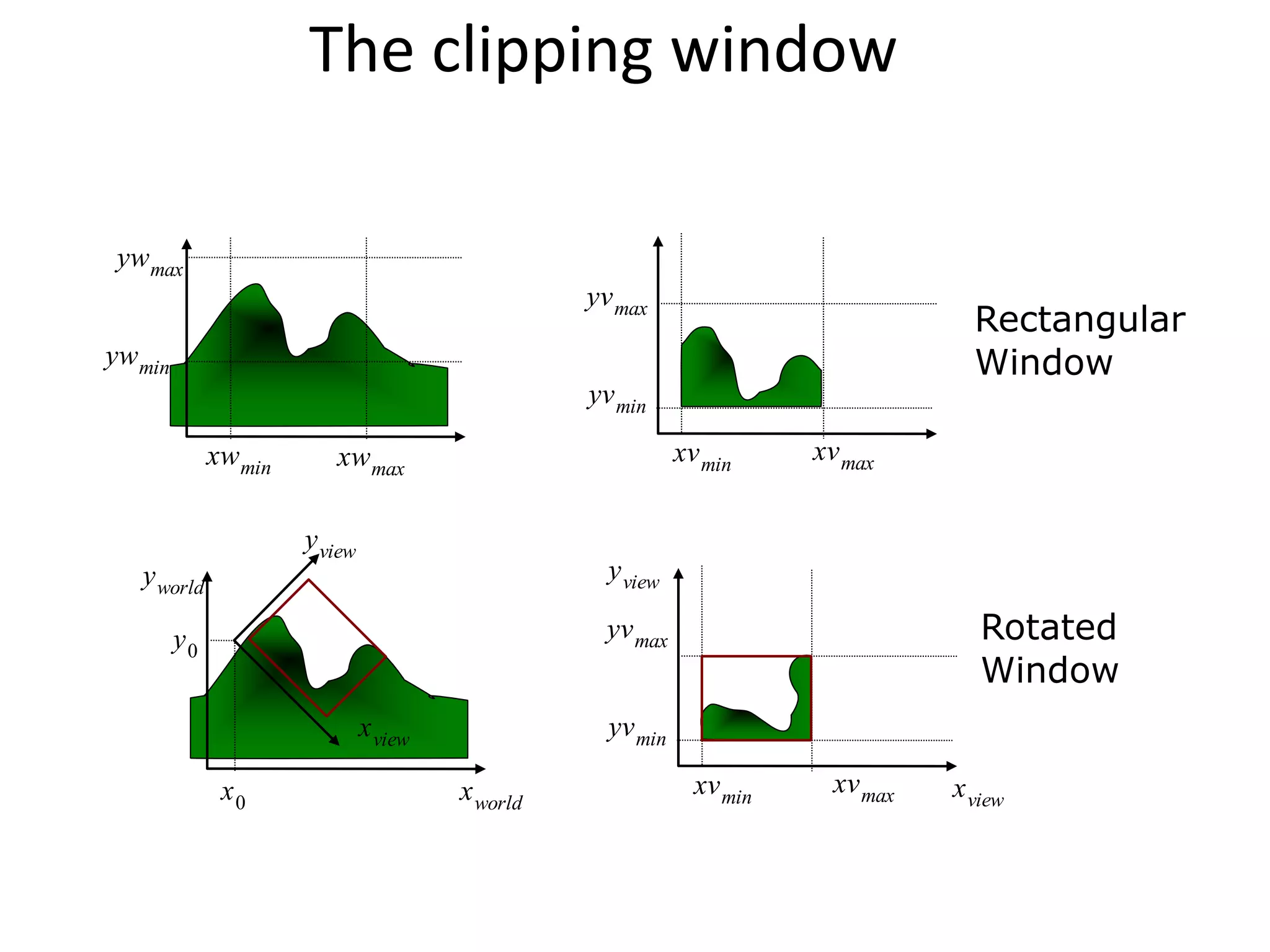
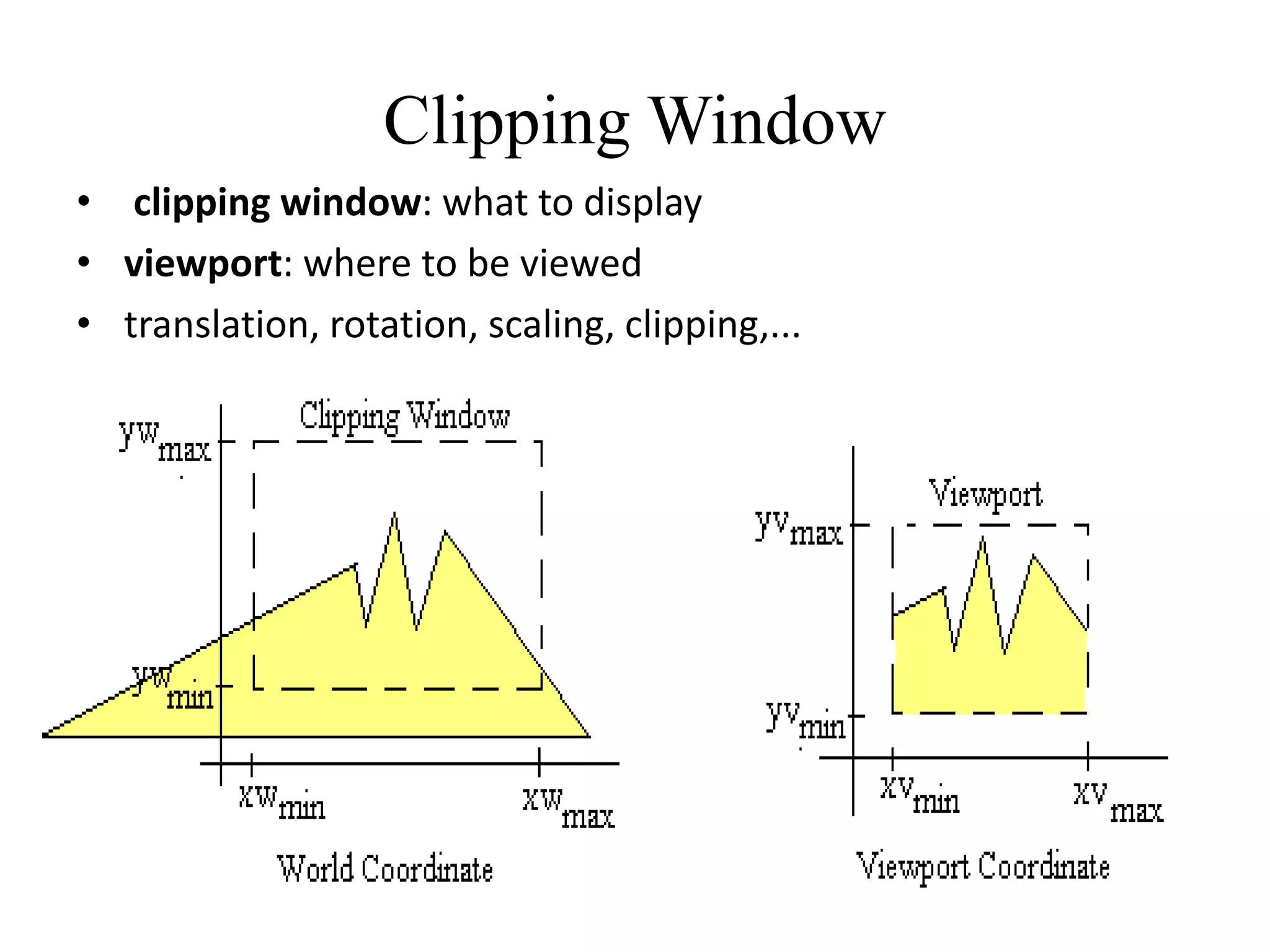
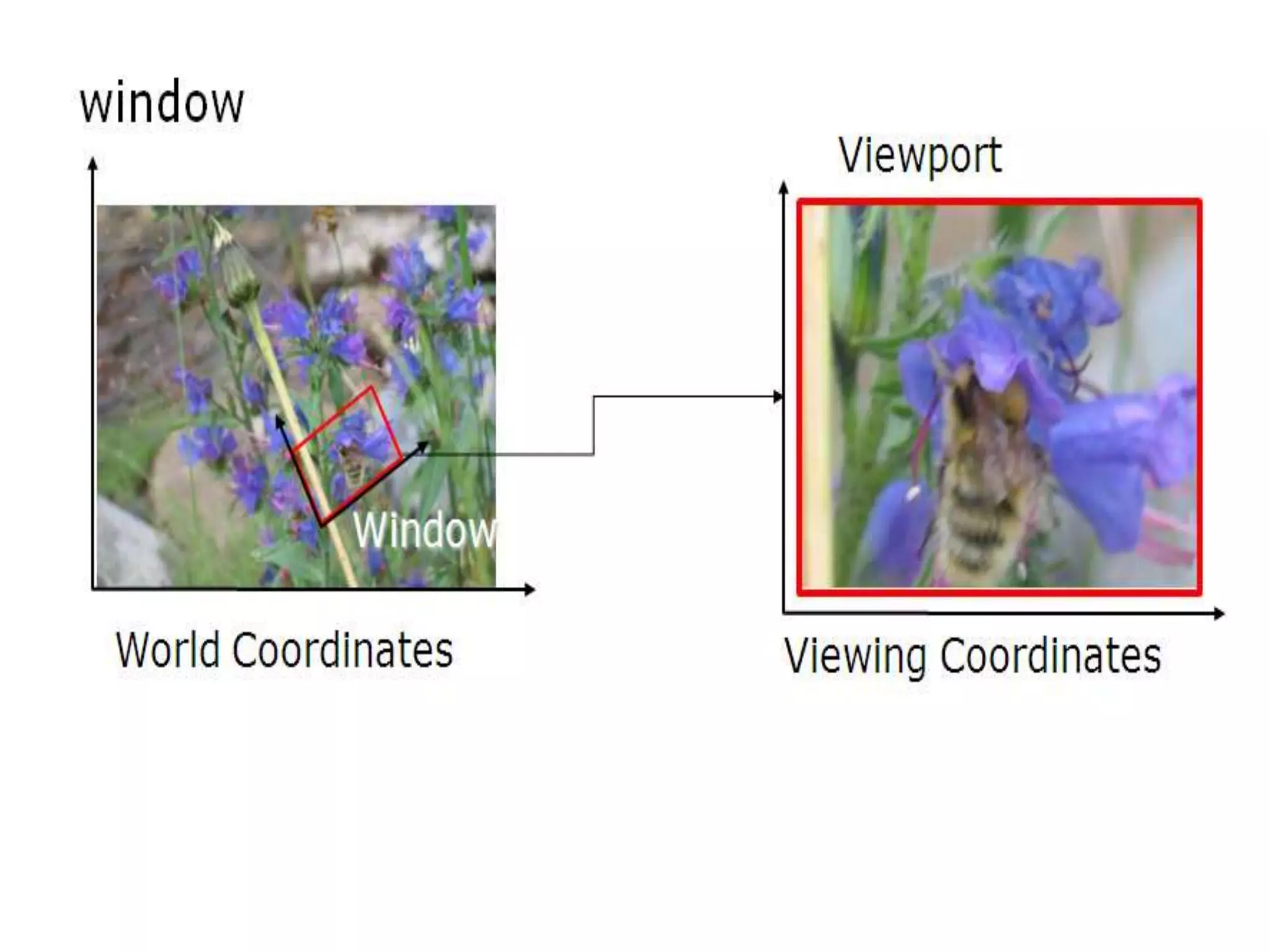
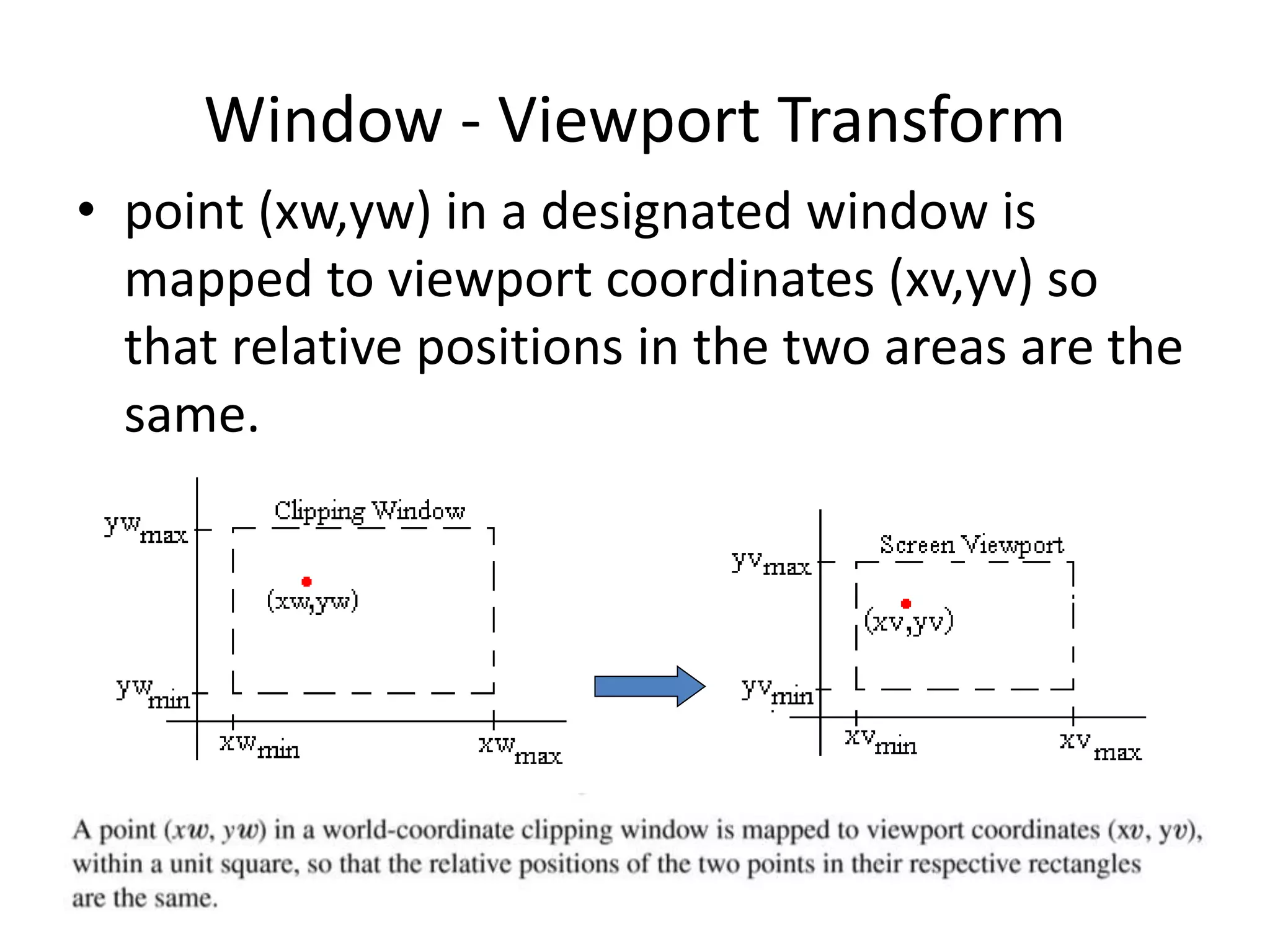
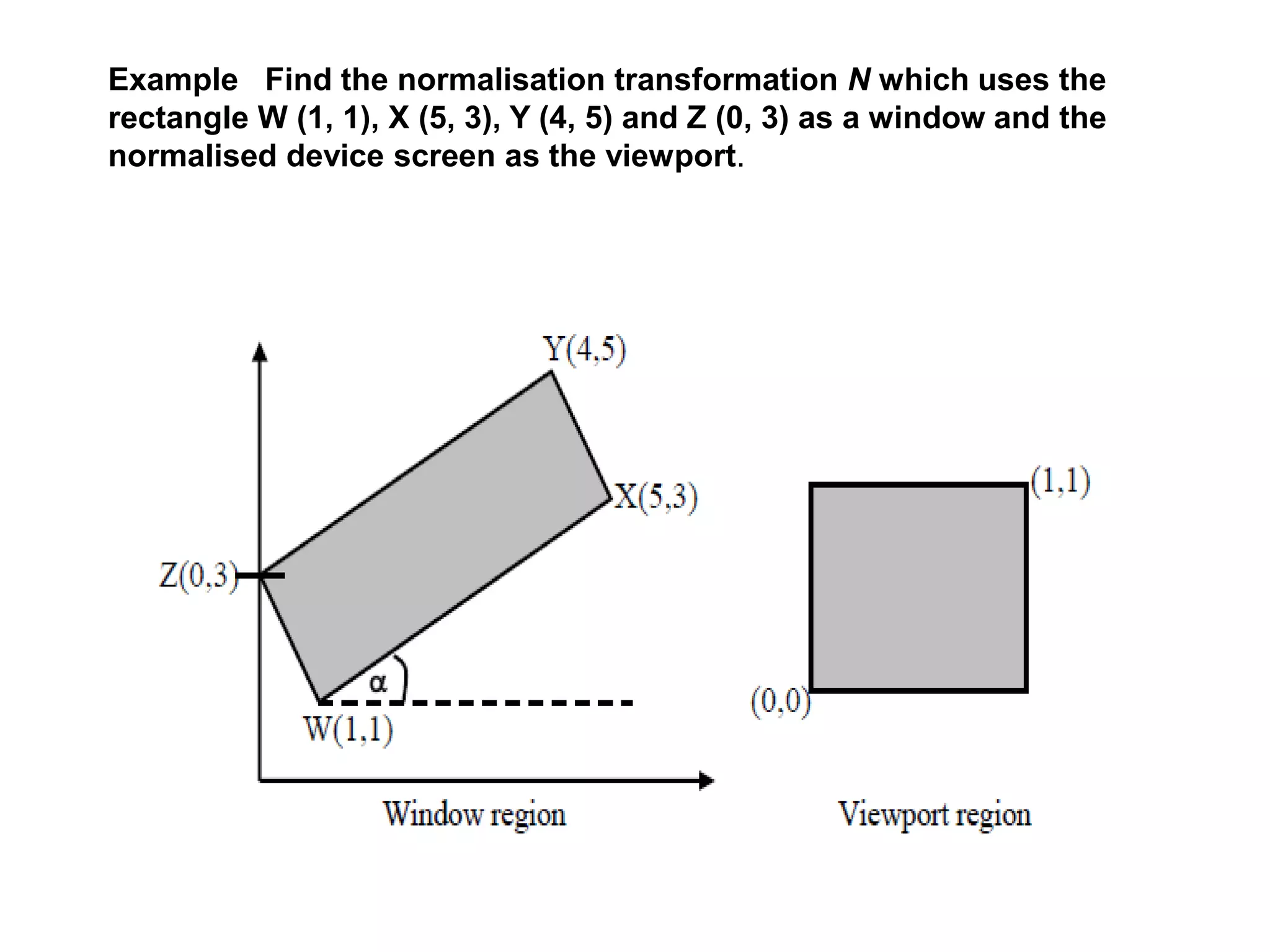
This document discusses windowing and clipping in computer graphics. It introduces key concepts such as: - A scene is defined using world coordinates, but only objects within the clipping window are displayed. - Clipping removes objects outside the window to optimize rendering time. - Graphics packages commonly use a rectangular clipping window aligned to axes for simplicity. - The clipping window defines what parts of the scene to display, while the viewport defines where on screen. 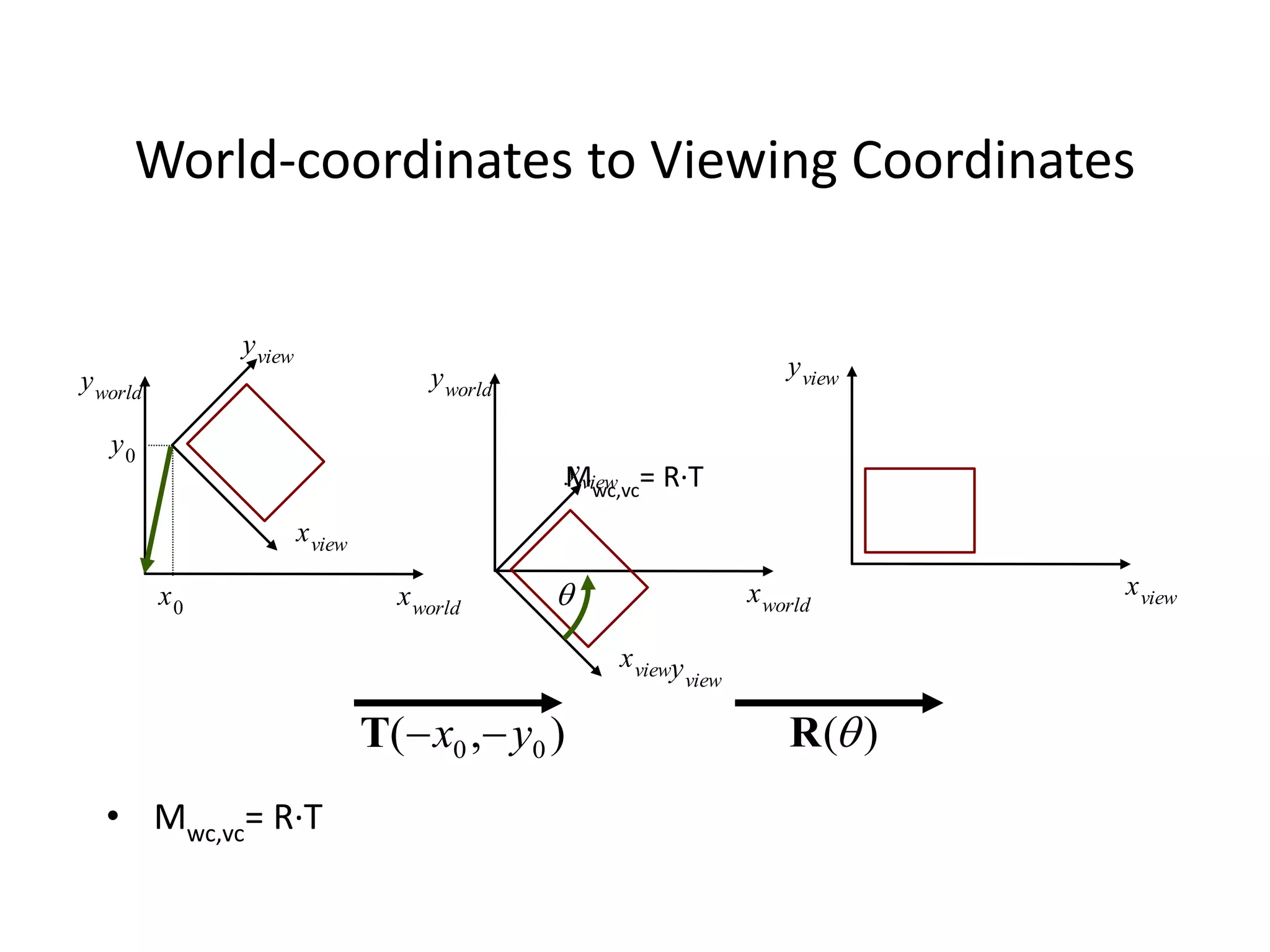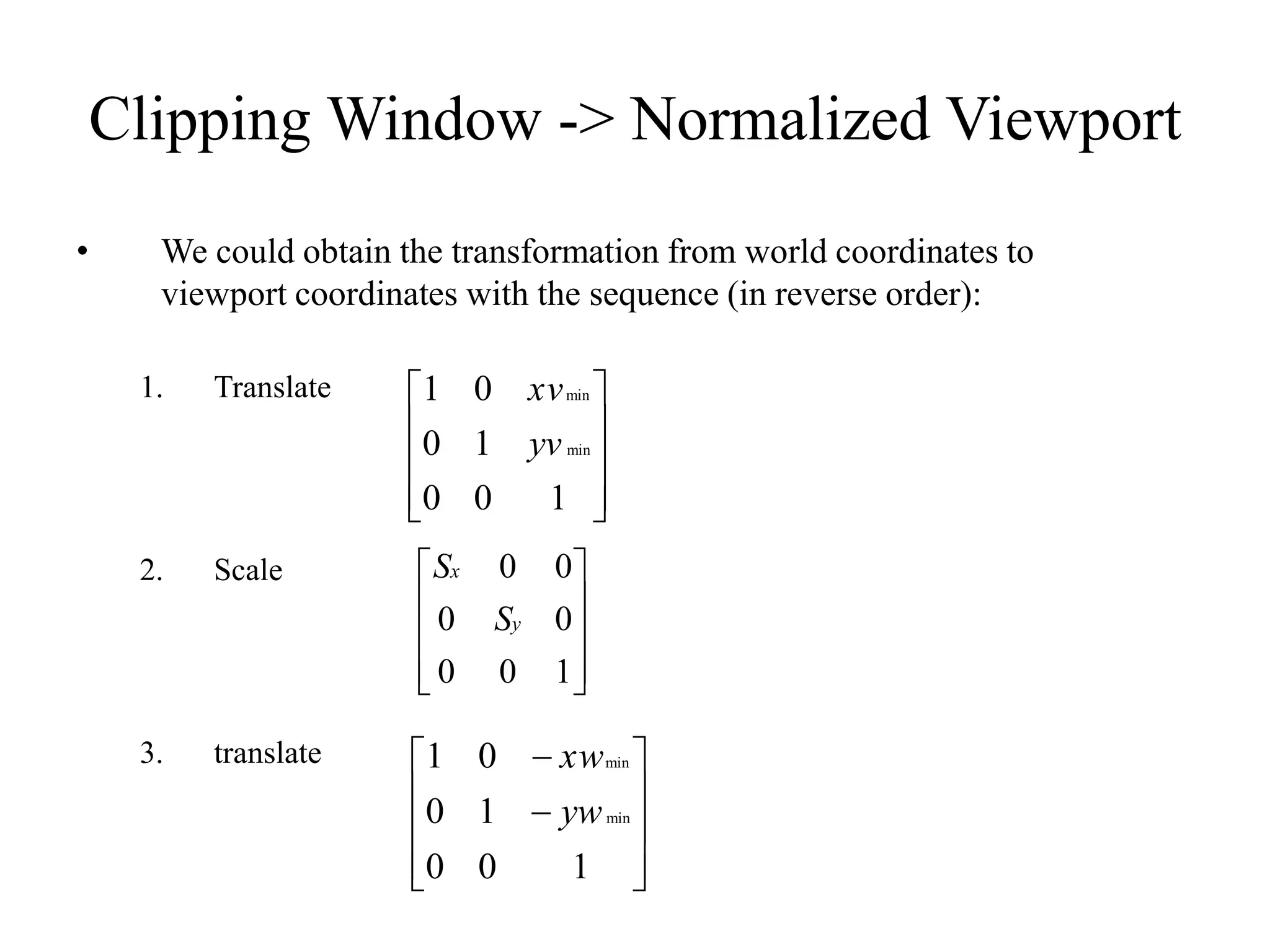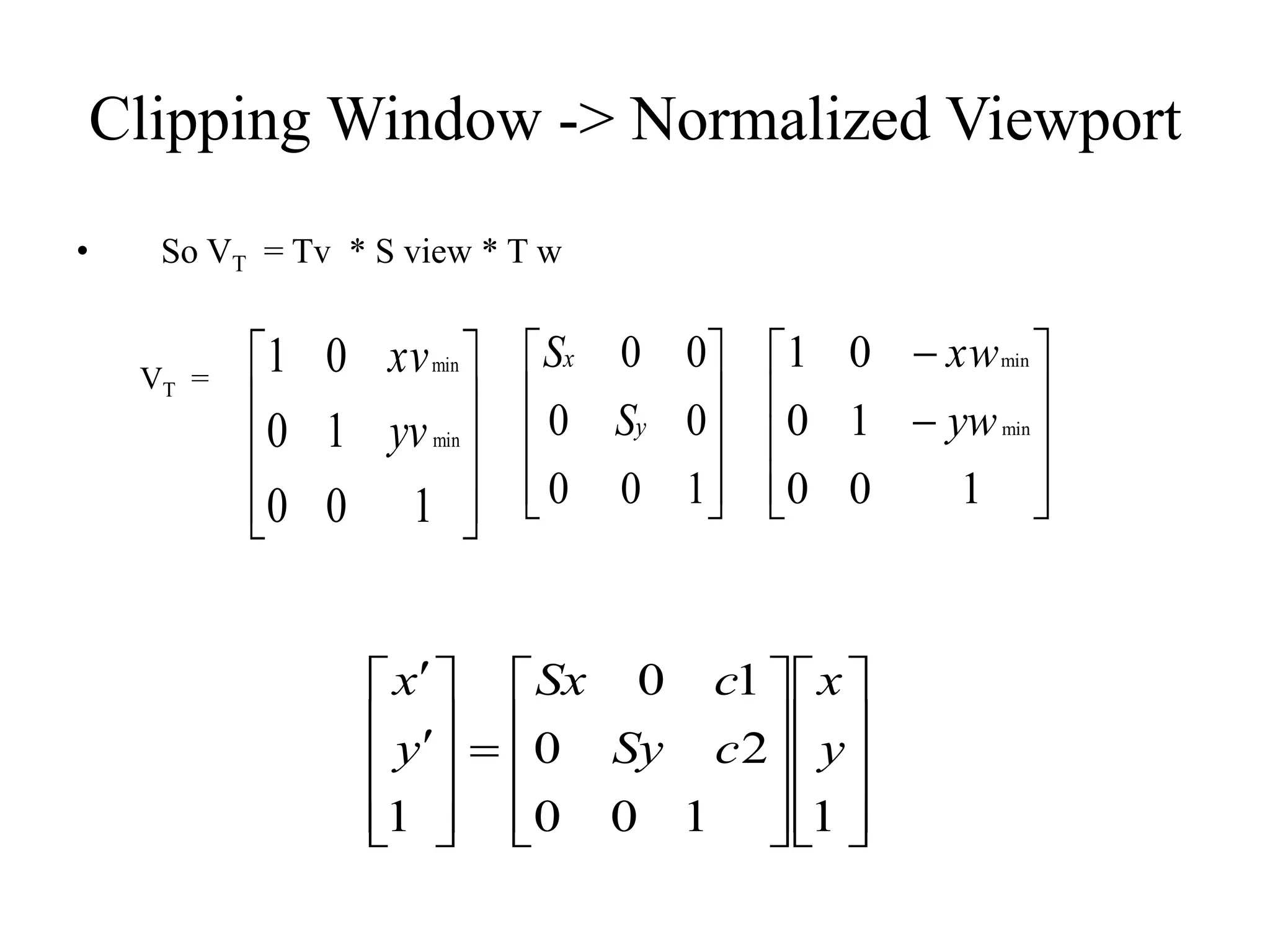- Transformations are used to map points from the clipping window to the normalized viewport. 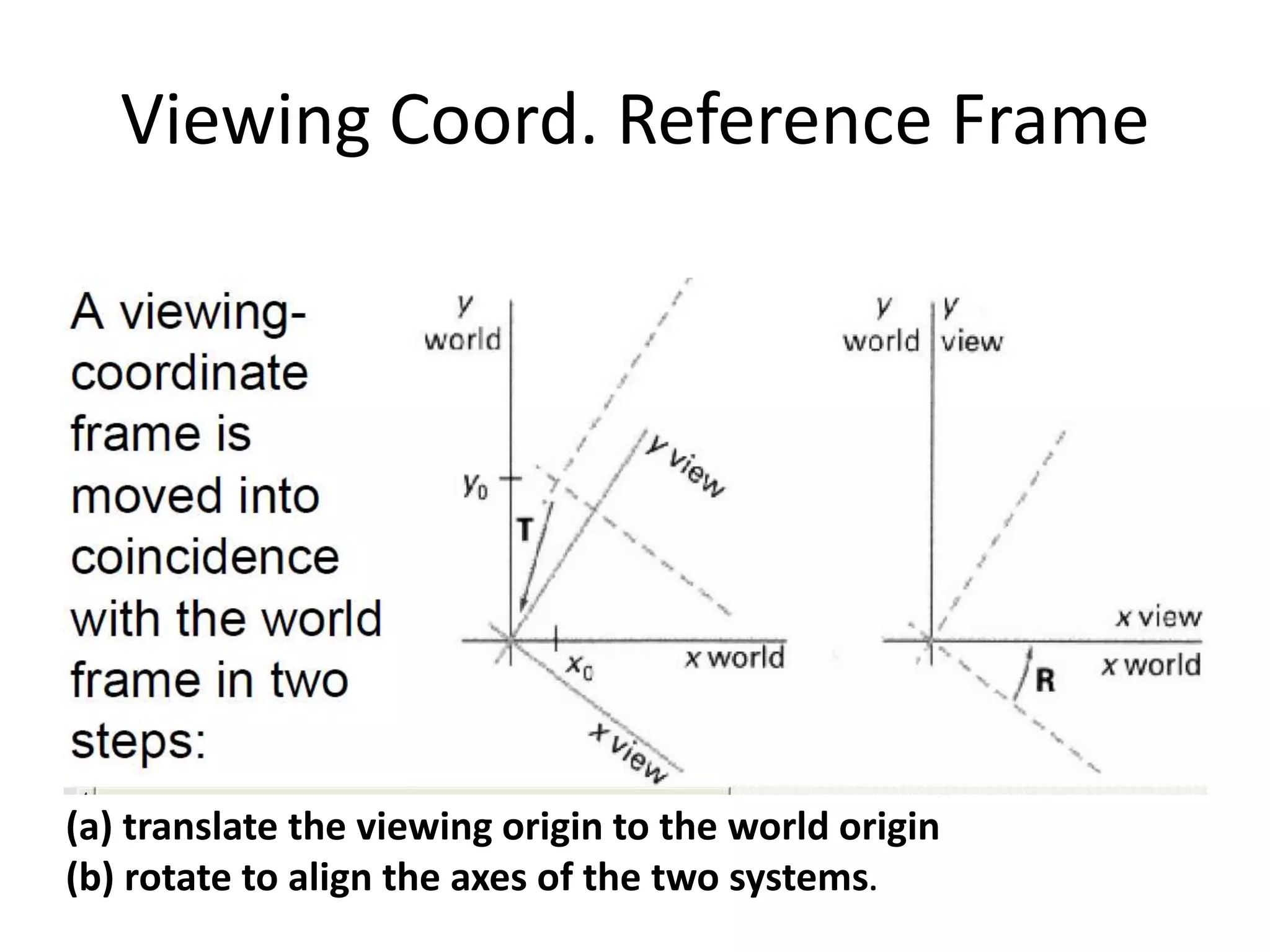The full transformation involves translating to the window origin, scaling to the viewport, and translating to the final viewport position. Rectangular clipping windows aligned to

1. Windowing I
• A scene is made up of a collection of objects specified in world
coordinates
World Coordinates

2. Windowing II
• When we display a scene only those objects within a particular
window are displayed
wymax
wymin
wxmin wxmax
Window
World Coordinates

3. Windowing III
• Because drawing things to a display takes time, we clip
everything outside the window
wymax
wymin
wxmin wxmax
World Coordinates
Window

4. Clipping Window
• We could design our own clipping window with any shape,
size and orientation.
• But clipping a scene using nonlinear boundaries requires more
processing than clipping against a rectangle.
• Therefore, graphics packages commonly allow only
rectangular clipping windows aligned with the x and y axes.

5. Window & Viewport
 Window/clipping window
 a world-coordinate area selected for display
 define what is to be viewed
 view port
 an area on a display device to which a window is
mapped
 define where it is to be displayed

6. Clipping Window
• clipping window: what to display
• viewport: where to be viewed
• translation, rotation, scaling, clipping,...

7. The viewing pipeline

8. The clipping window
xwmin xwmax
ywmin
ywmax
xvmin
xvmax
yvmin
yvmax
xvmin
xvmax
yvmin
yvmax
x0
y0
xview
yview
xworld
yworld
xview
yview
Rectangular
Window
Rotated
Window

10. Viewing Coord. Reference Frame
(a) translate the viewing origin to the world origin
(b) rotate to align the axes of the two systems.

11. World-coordinates to Viewing Coordinates
• Mwc,vc= R·T
x0
y0
xview
yview
xworld
yworld
xview
yview
xview
yview
xworld
yworld
yview
)
,
( 0
0 y
x 

T )
(
R

Mwc,vc= R·T

12. Window - Viewport Transform
• point (xw,yw) in a designated window is
mapped to viewport coordinates (xv,yv) so
that relative positions in the two areas are the
same.

13. Clipping Window -> Normalized Viewport
• To transform the world-coordinate point into the same relative
position within the viewport, we require that
min
max
min
min
max
min
min
max
min
min
max
min
yw
yw
yw
yw
yv
yv
yv
yv
xw
xw
xw
xw
xv
xv
xv
xv










For any point:
should hold.

14.   
  
min
max
min
max
min
min
min
max
min
max
min
min
yw
yw
yv
yv
yw
yw
+
yv
=
yv
xw
xw
xv
xv
xw
xw
+
xv
=
xv






• Solving these expressions for the viewport position (xv,yv) we
have:
where
)
(
)
(
min
min
min
min
yw
yw
s
yv
yv
xw
xw
s
xv
xv
y
x






min
max
min
max
min
max
min
max
yw
yw
yv
yv
s
xw
xw
xv
xv
s y
x







15. C
xw
s
xv
xw
s
xv
xw
s
xv
xw
s
xw
s
xv
xv
xw
xw
s
xv
xv
x
x
x
x
x
x











min)
min
min
min
min
min
(
)
(

































1
1
0
0
2
0
1
0
1
y
x
c
Sy
c
Sx
y
x
So The window to viewport transformation in matrix form can be
written as follows
When we solve it further we get…
)
(
)
(
min
min
min
min
yw
yw
s
yv
yv
xw
xw
s
xv
xv
y
x







16. • Note, if Sx = Sy then the relative proportions
of objects are maintained else the world
object will be stretched or contracted in either
x or y direction when displayed on output
device.

17. The complete window to viewport Transformation is a
compound transformation
That consists of the following 3 transformation.
• Translation on the window, to the origin i,e Tw
• Scaling i,e Sview
• Translation of scaled image to the place of the
Viewport, Tv

18. Clipping Window -> Normalized Viewport
• We could obtain the transformation from world coordinates to
viewport coordinates with the sequence (in reverse order):
1. Translate
2. Scale
3. translate










1
0
0
1
0
0
1
min
min
yv
xv










1
0
0
0
0
0
0
y
x
S
S












1
0
0
1
0
0
1
min
min
yw
xw

19. Clipping Window -> Normalized Viewport
• So VT = Tv * S view * T w
VT =










1
0
0
1
0
0
1
min
min
yv
xv










1
0
0
0
0
0
0
y
x
S
S












1
0
0
1
0
0
1
min
min
yw
xw

































1
1
0
0
2
0
1
0
1
y
x
c
Sy
c
Sx
y
x

21. Example Find the normalisation transformation N which uses the
rectangle W (1, 1), X (5, 3), Y (4, 5) and Z (0, 3) as a window and the
normalised device screen as the viewport.

22. • Here, we see that the window edges are not parallel to the
coordinate axes. So we will first rotate the window about W
so that it is aligned with the axes.
Here, we are rotating the rectangle in clockwise direction. So α is ( – )ve i.e., – α
The rotation matrix about W (1, 1) is,