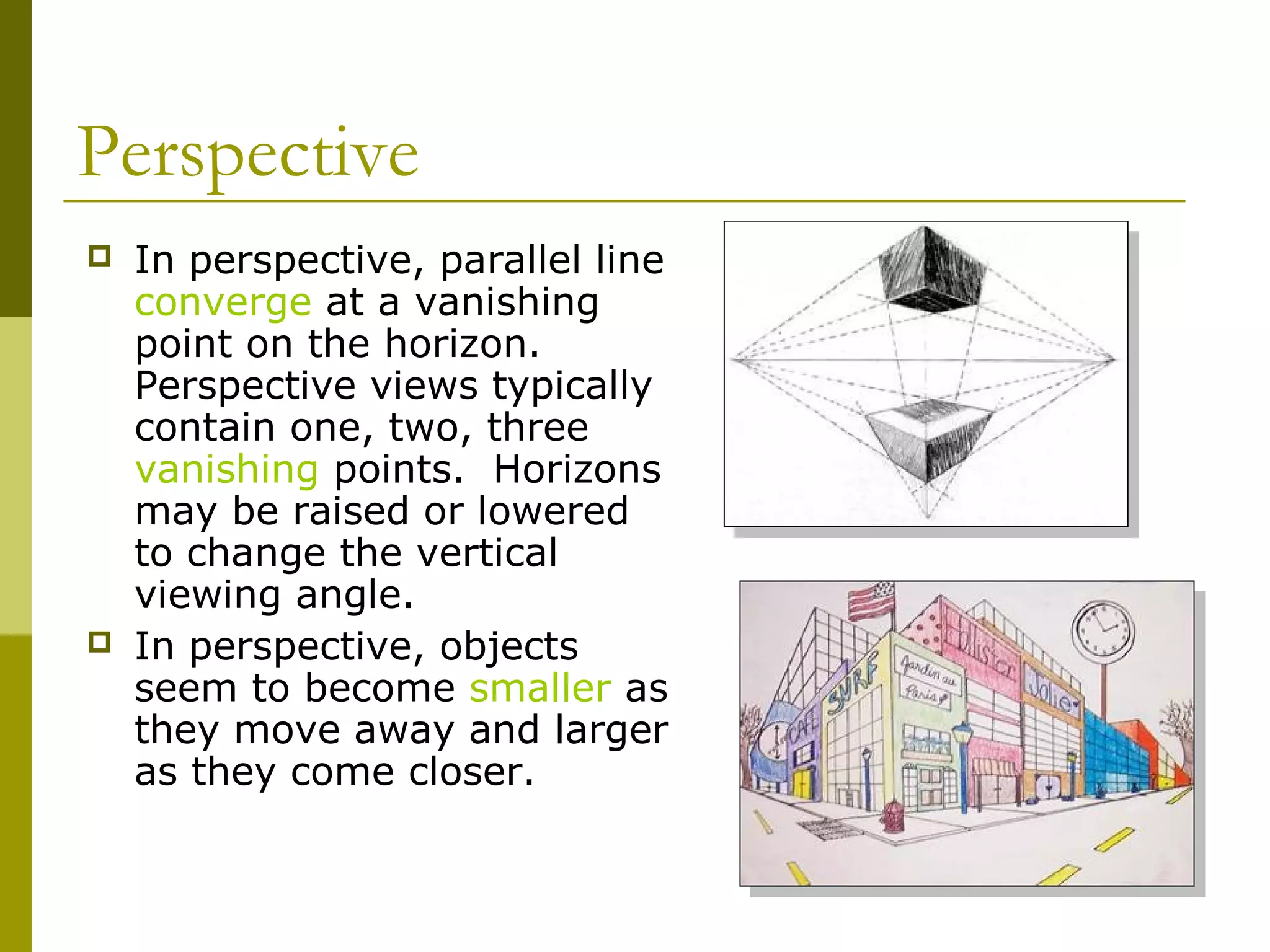
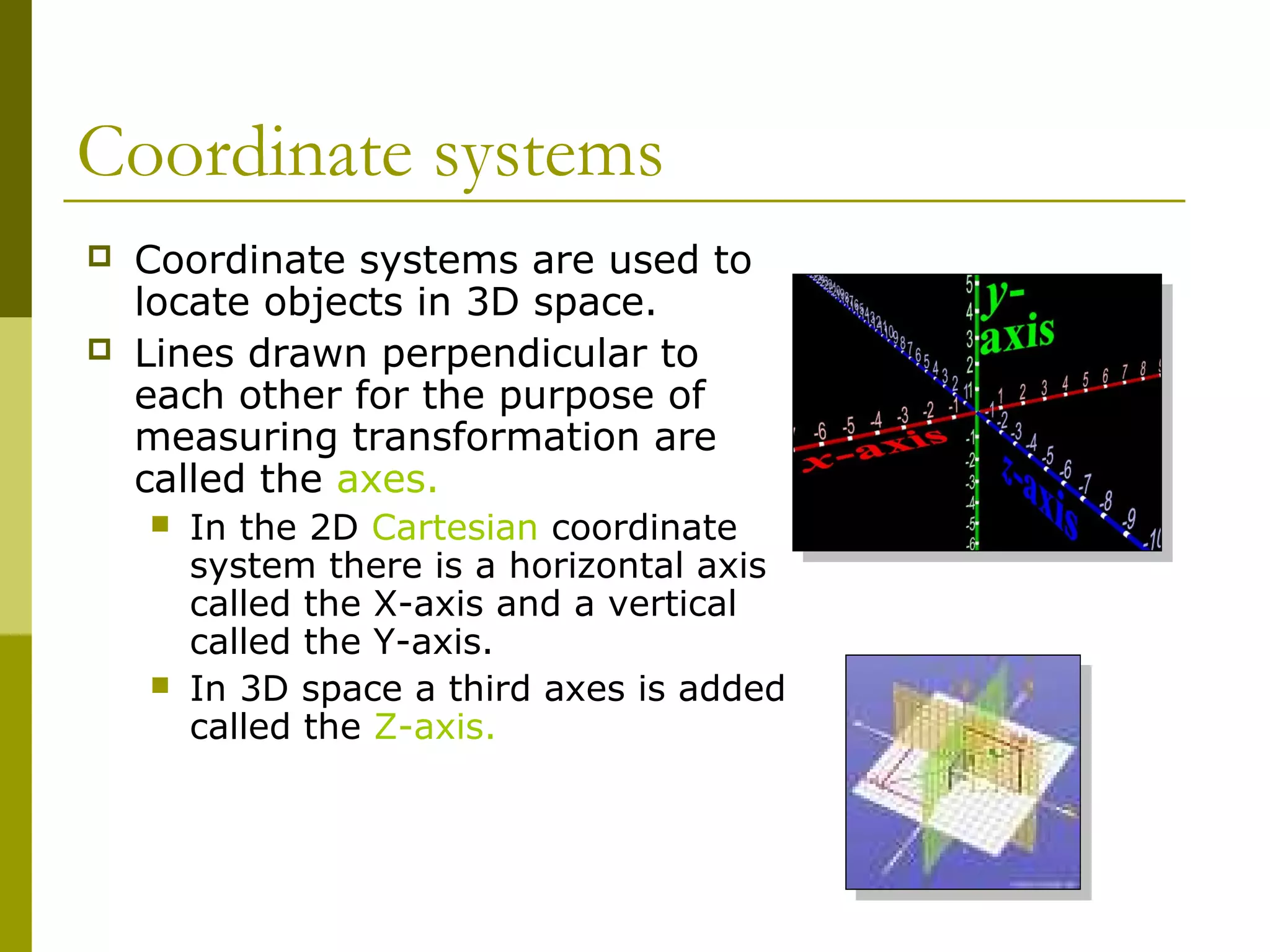
This document discusses different types of views and coordinate systems in 3D modeling programs. It explains that perspective views mimic human vision while orthographic views use parallel projection to show objects without convergence or diminishing size. Common views include top, front, side, and perspective. Coordinate systems locate objects in 3D space using perpendicular X, Y and Z axes. The origin is where the axes intersect. Views and coordinate systems are essential for accurately positioning and transforming objects in 3D modeling.

1. Navigating in 3D MAX
Guilford County SciVis
V106.02 part 1

2. Viewing Objects and/or Scenes
Depending upon the
software program, the
image on the monitor
could be a Perspective
view, an orthographic
view, or a combination.

3. Viewing Objects and/or Scenes
 3D Studio Max, Rhinoceros, and some other modeling
programs open with a four window display showing
top, side, and perspective viewports.
 Truespace opens with a single perspective view with
orthographic views available on demand.
 Most programs allow you to fill your display area with
any single viewport or varying multiple combinations
of display windows.

4. Viewing Objects and/or Scenes
 Various veiwports may be
formed by viewing angles.
 The image viewed depends
upon the line of sight of the
viewer.
 To move across a scene is
called panning.
 The scene may be rotated
about any of its three axes: x,
y, and, z.
 Views may be zoomed which
magnifies the image. The size
of the object is not increased.

5. Perspective
 Perspective mimics the way a human eye works and
provides scenes that have a “natural” appearance.
Perspective windows are included in all 3D modeling
programs.

6. Perspective
 In perspective, parallel line
converge at a vanishing
point on the horizon.
Perspective views typically
contain one, two, three
vanishing points. Horizons
may be raised or lowered
to change the vertical
viewing angle.
 In perspective, objects
seem to become smaller as
they move away and larger
as they come closer.

7. Perspective
 Objects seem to become
dimmer as they move
away. Atmospheric
features in the software can
be used to simulate
atmospheric density.
 Perspective viewports can
distort space and “fool the
eye” when trying to
position objects in 3D. It is
not a good idea to attempt
object placement and
alignment using the
perspective window alone.

8. Orthographic (Parallel Projection)
 Orthographic (Parallel Projection) viewports provide
an image in which the line of sight is perpendicular to
the picture plane.
 “Ortho” means straight. In orthographic
projection the projectors extend straight off of the
object, parallel to each other.
 Points on the object’s edges are projected onto a
picture plane where they form line on the plane.
The lines create a 2D image of the 3D object
being viewed.

9. Orthographic (Parallel Projection)
 Typically six different views can
be produced by orthographic
projection:
 Top, bottom, front, back, left,
and right sides.
 Lines and surfaces that are
inclined to the picture plane
appear as fore shortened edges
and surfaces on the plane to
which they are projected.
 Orthographic viewports are
extremely useful in the accurate
alignment and positioning of
objects and features with respect
to other features and objects .

10. Coordinate systems
 Coordinate systems are used to
locate objects in 3D space.
 Lines drawn perpendicular to
each other for the purpose of
measuring transformation are
called the axes.
 In the 2D Cartesian coordinate
system there is a horizontal axis
called the X-axis and a vertical
called the Y-axis.
 In 3D space a third axes is added
called the Z-axis.

11. Coordinate systems
 Where axes intersect is called
the origin. The coordinates
of the origin are 0,0 on the
2D plane and 0,0,0 in 3D
space.
 Numerical location placed
uniformly along the axes are
called the coordinates. These
numbers identify locations in
space. When written or
displayed, numbers are
always given in the order of
X first, then Y, the Z.

12. Coordinate systems
 Axes may be rotated or oriented
differently with in 3D space
depending upon whether you are
working with an individual
object, a viewport, or objects
within a scene.
 Local (user) coordinate system-
assign axes to particular object.
 World (global) coordinate
system-assign axes to the
scene.

13. Coordinate systems
 Many 3D modeling programs allow you to constrain
movement (rotation, scaling, and transformations)
along one axis, two` axes, or three axes.
 For example, you could lock the X- and Y-axes thereby
restricting movement of deformation to only a Z
direction.
 Relative coordinates are used to transform an object
starting at its current position.
 Absolute coordinates are used to transform an object
relative to the origin.

14. End Part I