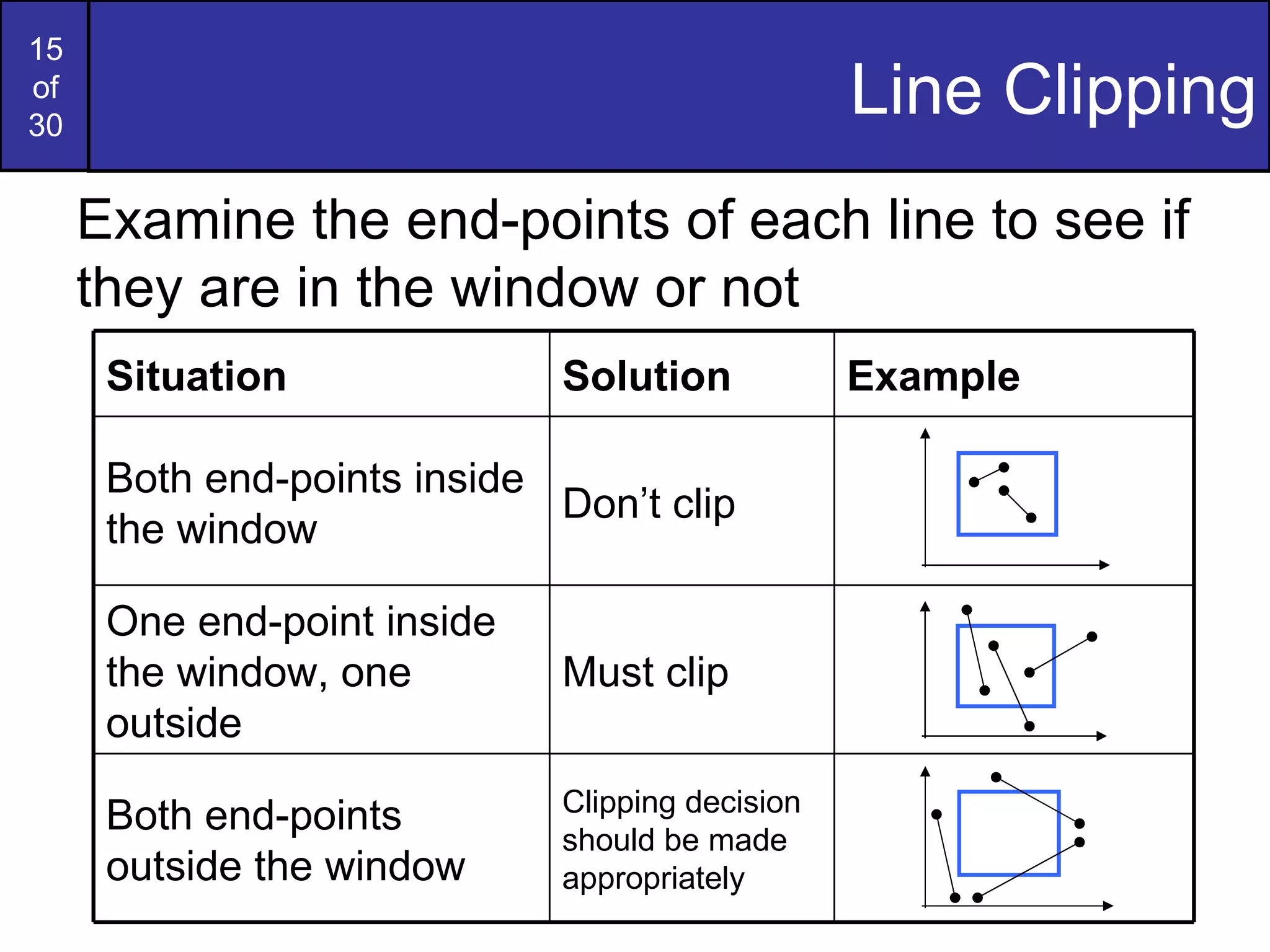
1. Clipping is a procedure that identifies parts of an image that are inside or outside a specified region, called the clip window. Parts inside the window are displayed, while outside parts are discarded. 2. There are different types of clipping like point, curve, text, and line clipping. Line clipping involves testing if line segments are fully inside/outside the window, and calculating intersections if they cross window boundaries. 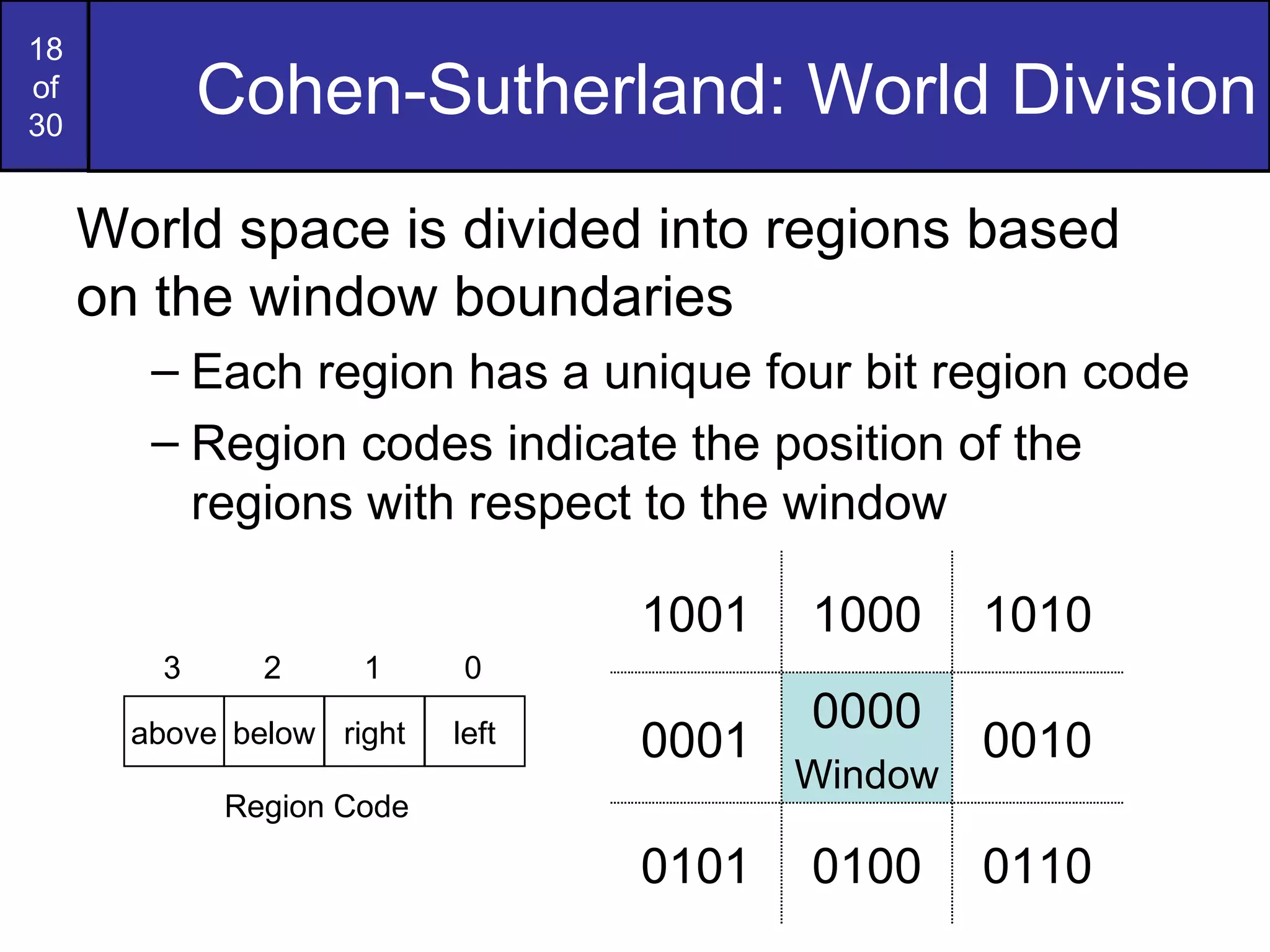3. Popular line clipping algorithms like Cohen-Sutherland and Liang-Barsky assign codes to line endpoints to quickly determine if lines are fully in/out of the window without calculating intersections. They find intersection points to clip lines that cross window edges.

1. 2D CLIPPING Clipping is a procedure that identifies those portions of a picture that are either inside or outside of a specified region of space. Clip Window is the region against which an object is to be clipped. It may be a polygon or curved boundaries. But rectangular clip regions are preferred. For viewing transformations, picture parts within window area are displayed. Everything outside window area is discarded.

2. CLIPPING (Cont…) Clipping algorithm – 2 methods Clipping applied in world coordinates & contents of window interior are mapped to device coordinates Eliminates processing necessary to transform those primitives outside window to device space Map complete world coordinate picture to device coordinate or normalized device coordinate, then clip against view port boundaries. Reduce calculations by allowing concatenation of viewing & geometric transformation matrices.

3. Types of clipping Based on different output primitives Point clipping Curve clipping Text clipping Exterior clipping Line clipping (Straight line segments) Area clipping (Polygons)

4. 1.POINT CLIPPING Clip window is a rectangle in standard position. A point p=(x,y) is saved for display, if the following inequalities are satisfied, xw min < x < xw max yw min < y < yw max where xw min, xw max , yw min & yw max are edges of clip window (WC window or view port boundaries) If any one of these 4 inequalities is not satisfied, the point is clipped i.e, not saved for display. Can be applied to scenes involving explosions or sea foam that are modeled with particles (points) distributed in some region of the scene.

5. 2.Curve clipping Curve clipping procedures will involve non-linear equations (so requires more processing than for objects with linear boundaries)

6. Curve clipping (cont) Preliminary test (Test for overlapping) The bounding rectangle for a circle or other curved object is used to test for overlap with a rectangular clip window. If the bounding rectangle is completely inside (save object), completely outside (discard the object) Both cases- no computation is necessary. If bounding rectangle test fails, use computation-saving approaches Circle – coordinate extents of individual quadrants & then octants are used for preliminary testing before calculating curve–window intersections Ellipse – coordinate extents of individual quadrants are used. If 2 regions overlap, solve the simultaneous line-curve equations to obtain the clipping intersection points.

7. 3.TEXT CLIPPING Depends on methods used to generate characters & the requirements of a particular application Methods for processing character strings relative to a window boundary, All-or-none string clipping strategy All or none character clipping strategy Clip the components of individual characters

8. TEXT CLIPPING (cont) All-or-none string clipping strategy Simplest method, fastest text clipping All string - inside clip window, keep it, otherwise discard. Bounding rectangle considered around the text pattern If bounding position of rectangle overlap with window boundaries, string is rejected. All or none character clipping strategy Discard or reject an entire character string that overlaps a window boundary i.e, discard those characters that are not completely inside the window. Compare boundary limits of individual characters with the window. Any character which is outside or overlapping the window boundary are clipped.

9. TEXT CLIPPING (cont)

10. TEXT CLIPPING (cont) Clip the components of individual characters Treat characters same as lines If individual char overlaps a clip window boundary, clip off the parts of the character that are outside the window. TEXT CLIPPING (cont)

11. 4.EXTERIOR CLIPPING Clip a picture to the exterior of a specified region The picture parts to be saved are those that are outside the region. Eg. Multiple window systems, applications that require overlapping pictures.

12. 5.Line Clipping For the image below consider which lines and points should be kept and which ones should be clipped wy max wy min wx min wx max Window P 1 P 2 P 3 P 6 P 5 P 7 P 10 P 9 P 4 P 8

13. Line clipping procedure A line clipping procedure involves several parts: Test a given line segment to determine whether it lies completely inside the clipping window. Determine whether it lies completely outside the window If not 1 & 2, perform intersection calculations with one or more clipping boundaries. A line with both endpoints inside all clipping boundaries is saved A line with both endpoints outside any one of the clip boundaries is discarded Other lines cross one or more clipping boundaries & require calculation of multiple intersection points

14. Point Clipping A point ( x,y ) is not clipped if: wx min ≤ x ≤ wx max AND wy min ≤ y ≤ wy max otherwise it is clipped wy max wy min wx min wx max Window P 1 P 2 P 5 P 7 P 10 P 9 P 4 P 8 Clipped Points Within the Window are Not Clipped Clipped Clipped Clipped

15. Line Clipping Examine the end-points of each line to see if they are in the window or not Situation Solution Example Both end-points inside the window Don’t clip One end-point inside the window, one outside Must clip Both end-points outside the window Clipping decision should be made appropriately

16. Line clipping – parametric test Performed if one or both endpoints of line segment are outside the clipping rectangle The parametric representation for line segment with endpoints (x1,y1) and (x2,y2) is given by X=x1+u (x2-x1) Y=y1+u (y2-y1), 0 < u < 1 Used to determine values for parameter u for intersections with the clipping boundary If u value (for intersection with a rectangle boundary edge) is outside the range 0 to 1, the line does not enter the interior of window boundary. If u is within the range o to 1, the line segment does indeed cross into the clipping area. This method is applied to each clipping boundary edge in turn to determine whether any part of the line segment is to be displayed. Clipping line segments with these parametric tests require a good deal of computation & faster approaches to clipping are possible.

17. Cohen-Sutherland Clipping Algorithm Oldest, most popular & efficient line clipping algorithm It reduces the number of line intersections that must be calculated by performing initial tests & speeds up processing Every line endpoint in a picture is assigned a 4-digit binary code called a region code Region code identifies the location of a point relative to the boundaries of the clipping rectangle

18. Cohen-Sutherland: World Division World space is divided into regions based on the window boundaries Each region has a unique four bit region code Region codes indicate the position of the regions with respect to the window 1001 1000 1010 0001 0000 Window 0010 0101 0100 0110 above below right left 3 2 1 0 Region Code

19. Cohen-Sutherland: Labelling Every end-point is labelled with the appropriate region code wy max wy min wx min wx max Window P 3 [0001] P 6 [0000] P 5 [0000] P 7 [0001] P 10 [0100] P 9 [0000] P 4 [1000] P 8 [0010] P 12 [0010] P 11 [1010] P 13 [0101] P 14 [0110]

20. Cohen-Sutherland: Lines In The Window Lines completely contained within the window boundaries have region code [0000] for both end-points so are not clipped wy max wy min wx min wx max Window P 3 [0001] P 6 [0000] P 5 [0000] P 7 [0001] P 10 [0100] P 9 [0000] P 4 [1000] P 8 [0010] P 12 [0010] P 11 [1010] P 13 [0101] P 14 [0110]

21. Cohen-Sutherland: Lines Outside The Window Any lines with a common set bit in the region codes of both end-points can be clipped The AND operation (result – not 0000) can efficiently check this wy max wy min wx min wx max Window P 3 [0001] P 6 [0000] P 5 [0000] P 7 [0001] P 10 [0100] P 9 [0000] P 4 [1000] P 8 [0010] P 12 [0010] P 11 [1010] P 13 [0101] P 14 [0110]

22. Cohen-Sutherland: Other Lines Lines that cannot be identified as completely inside or outside the window may or may not cross the window interior These lines are processed as follows: Compare an end-point outside the window to a boundary (choose any order in which to consider boundaries e.g. left, right, bottom, top) and determine how much can be discarded If the remainder of the line is entirely inside or outside the window, retain it or clip it respectively

23. Cohen-Sutherland: Other Lines (cont…) Otherwise, compare the remainder of the line against the other window boundaries Continue until the line is either discarded or a segment inside the window is found We can use the region codes to determine which window boundaries should be considered for intersection To check if a line crosses a particular boundary we compare the appropriate bits in the region codes of its end-points If one of these is a 1 and the other is a 0 then the line crosses the boundary

24. Cohen-Sutherland Examples Consider the line P 9 to P 10 below Start at P 10 From the region codes of the two end-points we know the line doesn’t cross the left or right boundary Calculate the intersection of the line with the bottom boundary to generate point P 10 ’ The line P 9 to P 10 ’ is completely inside the window so is retained wy max wy min wx min wx max Window P 10 [0100] P 9 [0000] P 10 ’ [0000] P 9 [0000]

25. Cohen-Sutherland Examples (cont…) Consider the line P 3 to P 4 below Start at P 4 From the region codes of the two end-points we know the line crosses the left boundary so calculate the intersection point to generate P 4 ’ The line P 3 to P 4 ’ is completely outside the window so is clipped wy max wy min wx min wx max Window P 4 ’ [1001] P 3 [0001] P 4 [1000] P 3 [0001]

26. Cohen-Sutherland Examples (cont…) Consider the line P 7 to P 8 below Start at P 7 From the two region codes of the two end-points we know the line crosses the left boundary so calculate the intersection point to generate P 7 ’ wy max wy min wx min wx max Window P 7 ’ [0000] P 7 [0001] P 8 [0010] P 8 ’ [0000]

27. Cohen-Sutherland Examples (cont…) Consider the line P 7 ’ to P 8 Start at P 8 Calculate the intersection with the right boundary to generate P 8 ’ P 7 ’ to P 8 ’ is inside the window so is retained wy max wy min wx min wx max Window P 7 ’ [0000] P 7 [0001] P 8 [0010] P 8 ’ [0000]

28. Calculating Line Intersections Intersection points with the window boundaries are calculated using the line-equation parameters Consider a line with the end-points ( x 1 , y 1 ) and ( x 2 , y 2 ) The y-coordinate of an intersection with a vertical window boundary can be calculated using: y = y 1 + m ( x boundary - x 1 ) where x boundary can be set to either wx min or wx max

29. Calculating Line Intersections (cont…) The x-coordinate of an intersection with a horizontal window boundary can be calculated using: x = x 1 + ( y boundary - y 1 ) / m where y boundary can be set to either wy min or wy max m is the slope of the line in question and can be calculated as m = ( y 2 - y 1 ) / ( x 2 - x 1 )

30. Liang-Barsky line clipping Faster line clipper Based on the analysis of parametric equation of a line segment of the form x=x1+u Δ x y=y1+u Δ y , 0<=u<=1 Δ x=x2-x1 & Δ y=y2-y1 More efficient Both Cohen-Sutherland and Liang-Barsky algorithm can be extended to 3-D clipping