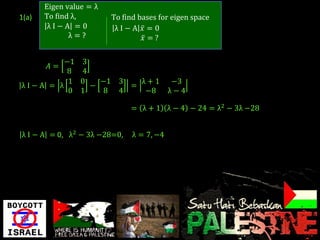
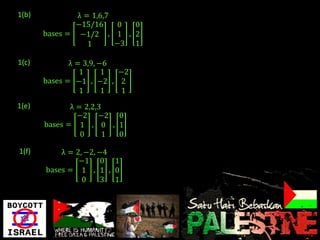
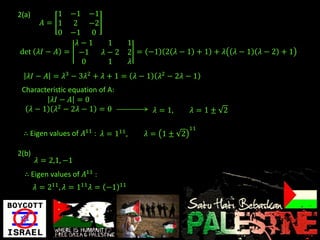
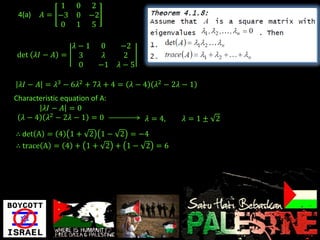
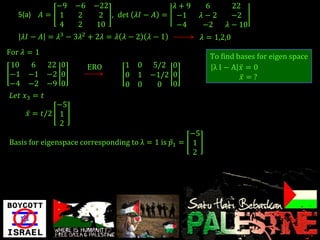
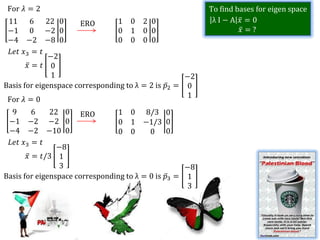
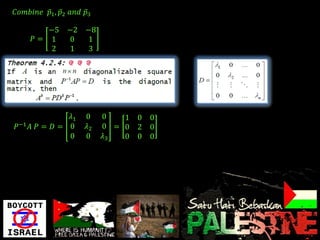
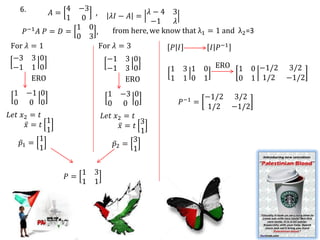
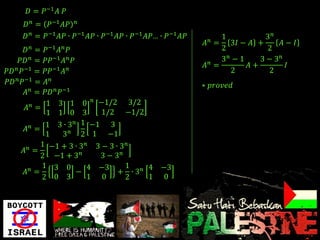
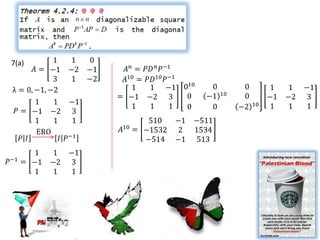
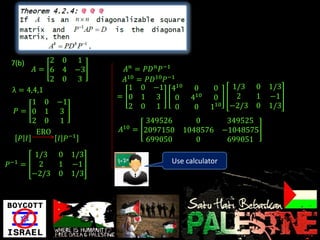
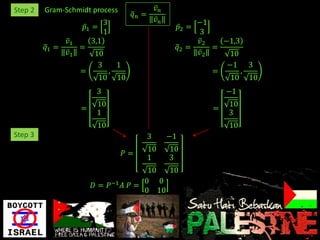
Eigenvalues and eigenvectors were found for several matrices. For a 3x3 matrix with eigenvalues 2, 2, 5, bases for the eigenspaces were determined to be the vectors [-5/2, 1, 2], [0, 1, 0], and [-8/3, 1, 3]. Another matrix was shown to be diagonalizable with eigenvalues 1, -1, 2 and change of basis matrix P.

2. TUTORIAL 8
MTH3201 LINEAR ALGEBRA

3. Eigen value = λ
1(a) To find λ, To find bases for eigen space
λI−A =0 λI−A 𝑥 =0
λ=? 𝑥 =?
−1 3
𝐴=
8 4
1 0 −1 3 λ+1 −3
λI−A = λ − =
0 1 8 4 −8 λ−4
= λ + 1 λ − 4 − 24 = λ2 − 3λ −28
λ I − A = 0, λ2 − 3λ −28=0, λ = 7, −4

4. when λ = 7, when λ = −4,
λI−A 𝑥 =0 λI−A 𝑥 =0
λ + 1 −3 𝑥1 0 λ + 1 −3 𝑥1 0
𝑥2 = 𝑥2 =
−8 λ − 4 0 −8 λ − 4 0
8 −3 𝑥1 0 −3 −3 𝑥1 0
𝑥2 = =
−8 3 0 −8 −8 𝑥2 0
8 −3 0 𝐸𝑅𝑂 1 −3/8 0 −3 −3 0 𝐸𝑅𝑂 1 1 0
−8 3 0 0 0 0 −8 −8 0 0 0 0
3 𝑥1 + 𝑥2 = 0
𝑥1 − 𝑥2 = 0
8 𝐿𝑒𝑡 𝑥2 = 𝑡
𝐿𝑒𝑡 𝑥2 = 𝑡 𝑥1 = −𝑡
3 t 3 −1
𝑥1 = 𝑡 ∴ 𝑥= ∴ 𝑥= 𝑡
8 8 8 1
3
∴ Hence, form a basis corresponding to λ = 7
8
−1
form a basis corresponding to λ = −4
1

5. 1(b) λ = 1,6,7
−15/16 0 0
bases = −1/2 , 1 , 2
1 −3 1
1(c) λ = 3,9, −6
1 1 −2
bases = −1 , −2 , 2
1 1 1
1(e) λ = 2,2,3
−2 −2 0
bases = 1 , 0 , 1
0 1 0
1(f) λ = 2, −2, −4
−1 0 1
bases = 1 , 1 , 0
0 3 1

6. 2 −6 1 0 2 −6 λ−2 6
1(d) 𝐴 = , λI−A = λ − =
4 −8 0 1 4 −8 −4 λ+8
= λ − 2 λ + 8 + 24 = λ2 + 6λ +8
λ I − A = 0, λ2 + 6λ +8=0, (λ+2)(λ+4)=0, λ = −2, −4
when λ = −2, when λ = −4,
−4 6 𝑥1 0 −6 6 𝑥1 0
= =
−4 6 𝑥2 0 −4 4 𝑥2 0
−4 6 0 𝐸𝑅𝑂 1 −3/2 0 −6 6 0 𝐸𝑅𝑂 1 −1 0
−4 6 0 0 0 0 −4 4 0 0 0 0
3 𝑥1 − 𝑥2 = 0
𝑥1 − 𝑥 =0
2 2
𝐿𝑒𝑡 𝑥2 = 𝑡
𝐿𝑒𝑡 𝑥2 = 𝑡 𝑥1 = 𝑡
3 t 3
𝑥1 = 𝑡 ∴ 𝑥= 1
2 ∴ 𝑥= 𝑡
2 2 1
3 1
∴ form a basis corresponding to λ = −2 ∴ form a basis corresponding to λ = −4
2 1

7. 2(a) 1
−1 −1
𝐴= 12 −2
0
−1 0
𝜆−1 1 1
det 𝜆𝐼 − 𝐴 = −1 𝜆−2 2 = −1 2 𝜆 − 1 + 1 + 𝜆 𝜆−1 𝜆−2 +1
0 1 𝜆
𝜆𝐼 − 𝐴 = 𝜆3 − 3𝜆2 + 𝜆 + 1 = 𝜆 − 1 𝜆2 − 2𝜆 − 1
Characteristic equation of A:
𝜆𝐼 − 𝐴 = 0
𝜆 − 1 𝜆2 − 2𝜆 − 1 = 0 𝜆 = 1, 𝜆 =1± 2
11
∴ Eigen values of 𝐴11 : 𝜆 = 111 , 𝜆 = 1± 2
2(b)
𝜆 = 2,1, −1
∴ Eigen values of 𝐴11 :
𝜆 = 211 , 𝜆 = 111 𝜆 = −1 11

8. 3(a) 3 −1 1
𝐴= 1 0 1
−5 2 −3
𝜆−3 1 −1
det 𝜆𝐼 − 𝐴 = −1 𝜆 −1
5 −2 𝜆 + 3
𝜆𝐼 − 𝐴 = 𝜆3 − 5𝜆 + 2 = 𝜆 − 2 𝜆2 + 2𝜆 − 1
Characteristic equation of A:
𝜆𝐼 − 𝐴 = 0
𝜆 − 2 𝜆2 + 2𝜆 − 1 = 0
𝜆 = 2, 𝜆 = −1 ± 2
∴ λ ≠ 0, A is invertible
3(b) 𝜆−5 −2 −6
det 𝜆𝐼 − 𝐴 = 0 𝜆+8 1
−1 2 𝜆
−9 ± 57
𝜆 = 6, 𝜆=
2
∴ λ ≠ 0, A is invertible

9. 1 0 2
4(a) 𝐴 = −3 0 −2
0 1 5
𝜆−1 0 −2
det 𝜆𝐼 − 𝐴 = 3 𝜆 2
0 −1 𝜆−5
𝜆𝐼 − 𝐴 = 𝜆3 − 6𝜆2 + 7𝜆 + 4 = 𝜆 − 4 𝜆2 − 2𝜆 − 1
Characteristic equation of A:
𝜆𝐼 − 𝐴 = 0
𝜆 − 4 𝜆2 − 2𝜆 − 1 = 0 𝜆 = 4, 𝜆 =1± 2
∴ det A = 4 1 + 2 1 − 2 = −4
∴ trace A = 4 + 1 + 2 + 1 − 2 = 6

10. 4(b) 𝜆 = 2, 𝜆 = −2 ± 2 3
∴ det A = 2 −2 + 2 3 −2 − 2 3 = −16
∴ trace A = 2 + −2 + 2 3 + −2 − 2 3 = −2
4(c) 𝜆 = 0, 𝜆 = −1 ± 2
∴ det A = 0
∴ trace A = −2
4(d) 𝜆 = 1, 𝜆 = 6, 𝜆=6
∴ det A = 36
∴ trace A = 13

11. −9 −6 −22 𝜆+9 6 22
5(a) 𝐴= 1 2 2 , det 𝜆𝐼 − 𝐴 = −1 𝜆−2 −2
4 2 10 −4 −2 𝜆 − 10
𝜆𝐼 − 𝐴 = 𝜆3 − 3𝜆2 + 2𝜆 = 𝜆 𝜆 − 2 𝜆−1 𝜆 = 1,2,0
For 𝜆 = 1
To find bases for eigen space
10 6 22 0 ERO 1 0 5/2 0 λI−A 𝑥 =0
−1 −1 −2 0 0 1 −1/2 0 𝑥 =?
−4 −2 −9 0 0 0 0 0
𝐿𝑒𝑡 𝑥3 = 𝑡
−5
𝑥 = 𝑡/2 1
2
−5
Basis for eigenspace corresponding to λ = 1 is 𝑝1 = 1
2

12. For 𝜆 = 2 To find bases for eigen space
11 6 22 0 ERO 1 0 2 0 λI−A 𝑥 =0
−1 0 −2 0 0 1 0 0 𝑥 =?
−4 −2 −8 0 0 0 0 0
𝐿𝑒𝑡 𝑥3 = 𝑡
−2
𝑥= 𝑡 0
1 −2
Basis for eigenspace corresponding to λ = 2 is 𝑝2 = 0
1
For 𝜆 = 0
9 6 22 0 ERO 1 0 8/3 0
−1 −2 −2 0 0 1 −1/3 0
−4 −2 −10 0 0 0 0 0
𝐿𝑒𝑡 𝑥3 = 𝑡
−8
𝑥 = 𝑡/3 1
3 −8
Basis for eigenspace corresponding to λ = 0 is 𝑝3 = 1
3

13. 𝐶𝑜𝑚𝑏𝑖𝑛𝑒 𝑝1 , 𝑝2 𝑎𝑛𝑑 𝑝3
−5 −2 −8
𝑃= 1 0 1
2 1 3
𝜆1 0 0 1 0 0
𝑃−1 𝐴 𝑃= 𝐷= 0 𝜆2 0 = 0 2 0
0 0 𝜆3 0 0 0

14. 5(b) 𝜆 = 2,2,5
For 𝜆 = 2 For 𝜆 = 5
0 0 0 0 3 0 0 0 ∴ Since A is 3X3 matrix,
1 0 0 0 1 3 0 0 there are only two basis vector.
−4 3 −3 0 −4 3 0 0 Thus, A is not diagonalizable
ERO ERO
1 0 0 0 1 0 0 0
0 1 −1 0 0 1 0 0
0 0 0 0 0 0 0 0
𝐿𝑒𝑡 𝑥3 = 𝑡 𝐿𝑒𝑡 𝑥3 = 𝑡
0 0
𝑥= 𝑡 1 𝑥= 𝑡 0
1 1
0 0
𝑝1 = 1 𝑝2 = 0
1 1

15. 5(c) 𝜆 = 1, −1,2
0 2 −1 𝜆1 0 0 1 0 0
−1
𝑃 = −1 −1 −1 , 𝑃 𝐴 𝑃= 𝐷= 0 𝜆2 0 = 0 −1 0
1 −1 2 0 0 𝜆3 0 0 2
5(d) 𝜆 = 1,4,9
−1 0 0 𝜆1 0 0 1 0 0
𝑃 = −1 1 −1 , 𝑃−1 𝐴 𝑃= 𝐷= 0 𝜆2 0 = 0 4 0
1 0 1 0 0 𝜆3 0 0 9

16. 6. 4 −3 𝜆−4 3
𝐴= , 𝜆𝐼 − 𝐴 =
1 0 −1 𝜆
1 0
𝑃−1 𝐴 𝑃 = 𝐷 = , from here, we know that λ1 = 1 and λ2 =3
0 3
For 𝜆 = 1 For 𝜆 = 3 𝑃 𝐼 𝐼 𝑃−1
−3 3 0 −1 3 0
−1 1 0 −1 3 0 1 3 1 0 ERO 1 0 −1/2 3/2
ERO ERO 1 1 0 1 0 1 1/2 −1/2
1 −1 0 1 −3 0 −1/2 3/2
0 0 0 0 0 0 𝑃−1 =
1/2 −1/2
𝐿𝑒𝑡 𝑥2 = 𝑡 𝐿𝑒𝑡 𝑥2 = 𝑡
1 3
𝑥= 𝑡 𝑥= 𝑡
1 1
1 3
𝑝1 = 𝑝2 =
1 1
1 3
𝑃=
1 1

17. 𝐷 = 𝑃−1 𝐴 𝑃
𝐷 𝑛 = 𝑃−1 𝐴𝑃 𝑛
𝐷 𝑛 = 𝑃−1 𝐴𝑃 ∙ 𝑃−1 𝐴𝑃 ∙ 𝑃−1 𝐴𝑃 ∙ 𝑃−1 𝐴𝑃… ∙ 𝑃−1 𝐴𝑃 𝑛
1 3𝑛
𝐴 = 3𝐼 − 𝐴 + 𝐴− 𝐼
𝐷𝑛= 𝑃−1 𝐴 𝑛 𝑃 2 2
𝑃𝐷 𝑛 = 𝑃𝑃−1 𝐴 𝑛 𝑃 3𝑛−1 3−3𝑛
𝐴𝑛 = 𝐴+ 𝐼
𝑃𝐷 𝑛 𝑃−1 = 𝑃𝑃−1 𝐴 𝑛 2 2
𝑃𝐷 𝑛 𝑃−1 = 𝐴𝑛 ∗ 𝑝𝑟𝑜𝑣𝑒𝑑
𝐴𝑛 = 𝑃𝐷 𝑛 𝑃−1
𝑛 1 3 1 0 𝑛 −1/2 3/2
𝐴 =
1 1 0 3 1/2 −1/2
𝑛 1 −1 3
𝑛 = 1 3∙3
𝐴
1 3 𝑛 2 1 −1
𝑛 =
1 −1 + 3 ∙ 3 𝑛 3 − 3 ∙ 3 𝑛
𝐴
2 −1 + 3 𝑛 3−3𝑛
1 3 0 4 −3 1 4 −3
𝐴𝑛 = − + ∙3𝑛
2 0 3 1 0 2 1 0

18. 7(a) 1 1 0
𝐴 = −1 −2 −1 𝐴𝑛 = 𝑃𝐷 𝑛 𝑃−1
3 1 −2 𝐴10 = 𝑃𝐷10 𝑃−1
λ = 0, −1, −2 1 1 −1 010 0 0 1 1 −1
10
= −1 −2 3 0 −1 0 −1 −2 3
1 1 −1 10
1 1 1 0 0 −2 1 1 1
𝑃 = −1 −2 3
1 1 1 510 −1 −511
10
ERO 𝐴 = −1532 2 1534
𝑃 𝐼 𝐼 𝑃−1 −514 −1 513
1 1 −1
𝑃−1 = −1 −2 3
1 1 1

19. 7(b) 2 0 1
𝐴 = 6 4 −3 𝐴 𝑛 = 𝑃𝐷 𝑛 𝑃−1
2 0 3 𝐴10 = 𝑃𝐷10 𝑃−1
λ = 4,4,1 1 0 −1 410 0 0 1/3 0 1/3
= 0 1 3 0 410 0 2 1 −1
1 0 −1 −2/3 0 1/3
2 0 1 0 0 110
𝑃= 0 1 3
2 0 1 349526 0 349525
10
ERO 𝐴 = 2097150 1048576 −1048575
𝑃 𝐼 𝐼 𝑃−1 699050 0 699051
1/3 0 1/3
𝑃−1 = 2 1 −1 Use calculator
−2/3 0 1/3

20. 8(a) 1 −3
𝐴=
−3 9
Step 1 λ = 0,10
For 𝜆 = 0 For 𝜆 = 10
−1 3 0 9 3 0
3 −9 0 3 1 0
ERO ERO
1 −3 0 1 1/3 0
0 0 0 0 0 0
𝐿𝑒𝑡 𝑥2 = 𝑡 𝐿𝑒𝑡 𝑥2 = 𝑡
3 −1
𝑥= 𝑡 𝑥 = 𝑡/3
1 3
3 −1
𝑝1 = 𝑝2 =
1 3

21. 8(a)
Step 2 Gram-Schmidt process 𝑣𝑛
𝑞𝑛 =
3 𝑣𝑛 −1
𝑝1 = 𝑝2 =
1 3
𝑣1 3,1 𝑣2 −1,3
𝑞1 = = 𝑞2 = =
𝑣1 10 𝑣2 10
3 1 −1 3
= , = ,
10 10 10 10
3 −1
10 10
= =
1 3
10 10
Step 3 3 −1
10 10
𝑃=
1 3
10 10
0 0
𝐷 = 𝑃−1 𝐴 𝑃=
0 10