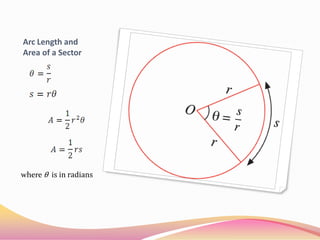
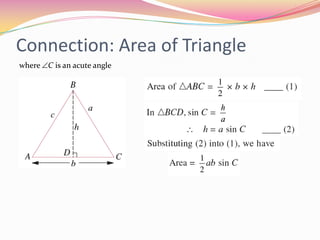
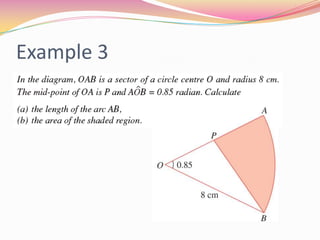
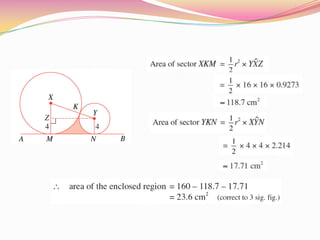
The document discusses calculating arc length and the area of a sector of a circle. It defines that the arc length s is equal to the radius r multiplied by the central angle θ in radians. The area of a sector is equal to (1/2) * r^2 * θ, where θ is in radians. It provides examples of calculating arc length when given r and θ, and the area of sectors when given r and the central angle measure.

1. Circular MeasureArc Length and Area of a Sector

2. Review: Radian MeasureIn general, if the length of arc, s units and the radius is r units, then That is the size of the angle (θ) is given by the ratio of the arc length to the length of the radius.For example:If s = 3 cm and r = 2 cm, then

3. Arc LengthFrom our definition of the radian, we have:s = rθwhere θ is in radiansFor example:If θ = 2.1 radians and r = 3 cmLength of arc AB, s = rθ= 3 × 2.1 cm= 6.3 cm

4. Example 1The diagram shows part of a circle, centre O, radius r cm. Calculate:The value of r,BOC in radians.In the sector AOB, s = 2.4 cm and θ= 1.2 radiansIn the sector BOC, s = 1.4 cm and r= 2 cm

5. Area of a SectorIn the diagram, the angle of the sector AOB is θradians.By proportion:rAsLet the area of sector AOB be A.Thus,rNow, as s = rθ, we have:

6. Example 2In the diagram, arc Ab and CD are arc of concentric circles, centre ). If OA = 6 cm, AC = 3 cm and the area of sector AOB is 12 cm2, calculateAOB in radians,The area and perimeter of the shaded region.Let be AOB = θ radiansArea of the sector AOB = 12 cm2(b) Now OC = OA + AC = 9 cmArea of the shaded region = area of sector COD – area of sector AOB= 27 – 12 = 15 cm2

7. Arc Length and Area of a Sectorwhere θ is in radians

8. Connection: Area of Trianglewhere C is an acute angle

9. Area of Trianglewhere C is an obtuse angle

10. Example 3

11. Solution:

12. Problem

13. Solutions