1) The function f(x) = 2x^2 + 8x + 6 can be written as f(x) = 2(x+2)^2 - 2. The maximum point is (-2, -2) and the equation of the tangent at this point is y = -2. 2) The function f(x) = -(x-4)^2 + h has a maximum point at (k, 9) so k = 4 and h = 9. 3) The function y = (x+m)^2 + n has an axis of symmetry at x = -m. Given the axis is x = 1, m = -1 and the minimum point is (1

1. SPM ZOOM–IN
Form 4: Chapter 1 Functions
4. (a) gf : x → x2 + 6x + 2
gf (x) = x2 + 6x + 2
g(x + 4) = x2 + 6x + 2
Paper 1
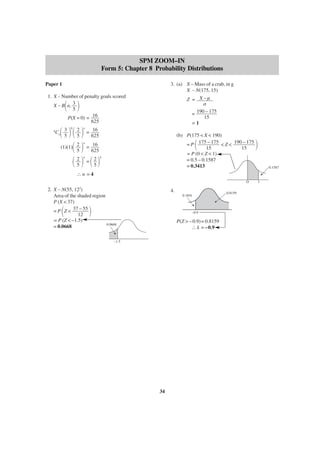
1. The relation in the given graph can be represented
using the following arrow diagram.
A
Let x + 4 = u
x=u–4
B
1
10
2
20
3
30
4
40
g(u) = (u – 4)2 + 6(u – 4) + 2
= u2 – 8u + 16 + 6u – 24 + 2
= u2 – 2u – 6
∴ g(x) = x2 – 2x – 6
[
Based on the above arrow diagram,
(a) the object of 40 is 3,
(b) the type of the relation is many-to-many
relation.
(b) fg(4) = f 42 – 2(4) – 6
= f(2)
=2+4
=6
2.
5. Let g–1(x) = y
g(y) = x
3y + k = x
x–k
y=
3
1
k
y = x–
3
3
1
k
∴ g–1(x) = x –
3
3
–4
–3
–2
2
3
4
16
9
4
(a) The above relation is a many-to-one relation.
(b) The function which represents the above
relation is f(x) = x2.
It is given that g–1(x) = mx –
5
6
Hence, by comparison,
1
k
5
5
m = and – = – ⇒ k =
3
3
6
2
3. f 2 (x) = ff (x)
= f (px + q)
= p (px + q) + q
= p2 x + pq + q
It is given that f 2 (x) = 4x + 9
By comparison,
p2 = 4
pq + q
p =–2
–2q + q
–q
q
]
=9
=9
=9
= –9
The question
requires p < 0.
1

2. Paper 2
2. (a) Let f –1(x)
f(y)
y
–2
2
y
2
y
y
∴ f –1(x)
∴ f –1(3)
hx
x–3
hx
f(x) =
x–3
1. (a) f : x →
Let f –1(x)
f(y)
hy
y–3
hy
hy
3x
3x
=y
=x
=x
= 2(x + 2)
= 2x + 4
= 2x + 4
= 2(3) + 4 = 10
Hence, by comparison,
2k + 4 = –4
2k = –8
k = –4
kx
, x ≠ 2.
x–2
Hence, by comparison, h = 2 and k = 3.
[
(c) hf(x) : x → 9x – 3
h[f(x)] = 9x – 3
x
h – 2 = 9x – 3
2
x
Let
–2 =u
2
x
=u+2
2
x = 2u + 4
]
gf –1(x) = g f –1(x)
3x
=g
x–2
΂
΂
΃
1
3x
x–2
x–2
=
3x
gf –1(x) = –5x
x–2
= –5x
3x
x – 2 = –15x2
2
15x + x – 2 = 0
(3x – 1)(5x + 2) = 0
1
2
x = or –
3
5
(
=x+2
But it is given that
f –1g : x → 6x – 4
f –1g (x) = 6x – 4
But it is given that f –1(x) =
=
=x
(b) f –1g(x) = f –1[g(x)]
= f –1(3x + k)
= 2(3x + k) + 4
= 6x + 2k + 4
= x (y – 3)
= xy – 3x
= xy – hy
= y(x – h)
3x
y=
x–h
3x
∴ f –1 (x) =
x–h
(b)
=y
=x
)
΃
h(u) = 9(2u + 4) – 3
= 18u + 33
∴ h : x → 18x + 33
2

3. SPM Zoom-In
Form 4: Chapter 2 Quadratic Equations
Paper 1
1.
4. x2 + 2x – 1 + k(2x + k) = 0
x2 + 2x – 1 + 2kx + k2= 0
x2 + 2x + 2kx + k2 – 1= 0
x2 + (2 + 2k)x + k2 – 1 = 0
12x2 – 5x(2x – 1) = 2(3x + 2)
12x2 – 10x2 + 5x = 6x + 4
2
12x – 10x2 + 5x – 6x – 4 = 0
2x2 – x – 4 = 0
x=
–b Ϯ
x=
–(–1) Ϯ
a = 1, b = 2 + 2k, c = k2 – 1
b2 – 4ac
2a
If a quadratic equation has two real and distinct
roots, then b2 – 4ac > 0.
(–1)2 – 4(2)(–4)
2(2)
b2 – 4ac > 0
(2 + 2k) – 4(1)(k2 – 1) > 0
4 + 8k + 4k2 – 4k2 + 4 > 0
8k + 8 > 0
8k > –8
k > –1
2
1 Ϯ 33
4
x = 1.6861 or –1.1861
x=
΂ ΃
Product of roots = ΂– 2 ΃΂– 3 ΃ = 2
3
5
5
2. Sum of roots = – 2 + – 3 = – 19
3
5
15
5.
a = 3, b = –2m, c = 12
The required quadratic equation is
x2 + 19 x + 2 = 0
15
5
If a quadratic equation has equal roots, then
b2 – 4ac = 0.
b2 – 4ac = 0
(–2m) – 4(3)(12) = 0
4m2 – 144 = 0
4m2 = 144
m2 = 36
m = ±6
x2 – (sum of roots)x + (product of roots) = 0
2
15x2 + 19x + 6 = 0
3. 3x2 + 4p + 2x = 0
3x2 + 2x + 4p = 0
a = 3, b = 2, c = 4p
If a quadratic equation does not have real roots,
then b2 – 4ac < 0.
<0
<0
<0
< –4
p > –4
–48
p> 1
12
b2 – 4ac
2 – 4(3)(4p)
4 – 48p
–48p
2
3(x2 + 4) = 2mx
3x2 + 12 = 2mx
2
3x – 2mx + 12 = 0
3

4. 6. x2 + 2x – 8 = 0
a = 1, b = 2, c = –8
7. x2 – (k + 2)x + 2k = 0
a = 1, b = –(k + 2), c = 2k
If one of the roots is α, then the other root is 2α.
The roots are p and q.
Sum of roots = – b
a
p + q = –2
1
p + q = –2
Sum of roots = – b
a
΂
α + 2α = – –(k + 2)
1
3α = k + 2
α = k+2 …
3
Product of roots = c
a
pq = – 8
1
΃
1
Product of roots = c
a
2α2 = 2k
1
pq = –8
The new roots are 2p and 2q.
Sum of new roots
= 2p + 2q
= 2(p + q)
= 2(–2)
= –4
α2 = k …
1
Substituting
΂ k+2΃
3
2
Product of new roots
= (2p)(2q)
= 4pq
= 4(–8)
= –32
(k + 2)2
9
(k + 2)2
k2 + 4k + 4
k2 – 5k + 4
(k – 1)(k – 4)
k
The quadratic equation that has the roots 2p and
2q is x2 + 4x – 32 = 0.
4
into
2
=k
=k
= 9k
= 9k
=0
=0
= 1 or 4
2
:

5. Paper 2
From 1 :
When m = 2,
6(2) = k – 3
k = 12 + 3
k = 15
1. (2x – 1)(x + 3) = 2x – 3 – k
2x2 + 6x – x – 3 = 2x – 3 – k
2x2 + 3x + k = 0
a = 2, b = 3, c = k
3. (a) 2x2 + px + q = 0
a = 2, b = p, c = q
The roots are –2 and p.
Sum of roots = – b
a
–2 + p = – 3
2
–p = – 3 + 2
2
p = 1
2
The roots are – 3 and 2.
2
Sum of roots = – b
a
p
–3 +2 =–
2
2
1 =– p
2
2
p = –1
Product of roots = c
a
–2p = k
2
Product of roots = c
a
΂ ΃
–2 1 = k
2
2
k = –2
q
– 3 ϫ2=
2
2
q = –6
2. 2x2 + (3 – k)x + 8m = 0
a = 2, b = 3 – k, c = 8m
(b)
2x2 – x – 6 = k
2x – x – 6 – k = 0
a = 2, b = –1, c = –6 – k
2
The roots are m and 2m.
Sum of roots = – b
a
m + 2m = – 3 – k
2
6m = k – 3 …
If the quadratic equation does not have real
roots, then b2 – 4ac < 0.
< 0,
<0
<0
< –49
49
k <–
8
1
k < –6
8
When
b2 – 4ac
2
(–1) – 4(2)(–6 – k)
1 + 48 + 8k
8k
1
Product of roots = c
a
m(2m) = 8m
2
2m2 = 4m
m2 = 2m
2
m – 2m = 0
m(m – 2) = 0
m = 0 or 2
m = 0 is not accepted.
∴m =2
5

6. SPM ZOOM–IN
Form 4: Chapter 3 Quadratic Functions
Paper 1
1. f(x) = 2x2 + 8x + 6
= 2(x2 + 4x + 3)
4 2
4
= 2 x2 + 4x +
–
2
2
= 2(x2 + 4x + 22 – 22 + 3)
= 2[(x + 2)2 – 1]
= 2(x + 2)2 – 2
∴ a = 2, p = 2, q = –2
[
–1
΂ ΃ ΂ ΃ + 3]
2
p
5
Hence, the required range of values of p is
p < –1 or p > 5.
5. 3x2 + hx + 27 = 0
a = 3, b = h, c = 27
If a quadratic equation does not have real roots,
b2 – 4ac < 0
2
h – 4(3) (27) < 0
h2 – 324 < 0
(h + 18)(h – 18) < 0
2. From f(x) = – (x – 4)2 + h, we can state that the
coordinates of the maximum point are (4, h). But it
is given that the coordinates of the maximum point
are (k, 9). Hence, by comparison,
(a) k = 4
(b) h = 9
(c) The equation of the tangent to the curve at its
maximum point is y = 9.
h
–18
3. (a) y = (x + m)2 + n
The axis of symmetry is x = –m.
But it is given that the axis of symmetry is
x = 1.
∴ m = –1
Hence, the required range of values of h is
–18 < h < 18.
6. g(x) = (2 – 3k)x2 + (4 – k)x + 2
a = 2 – 3k, b = 4 – k, c = 2
When m = –1, y = (x – 1)2 + n
Since the y-intercept is 3, the point is (0, 3).
∴ 3 = (0 – 1)2 + n
n =2
If a quadratic curve intersects the x-axis at two
distinct points, then
b2 – 4ac > 0
2
(4 – k) – 4(2 – 3k)(2) > 0
16 – 8k + k2 – 16 + 24k > 0
k2 + 16k > 0
k(k + 16) > 0
(b) When m = –1 and n = 2,
y = (x – 1)2 + 2
Hence, the minimum point is (1, 2).
4.
18
(2 + p)(6 – p) < 7
12 + 4p – p2 – 7 < 0
–p2 + 4p + 5 < 0
p2 – 4p – 5 > 0
(p + 1)(p – 5) > 0
–16
0
k
Hence, the required range of values of k is
k < –16 or k > 0.
6

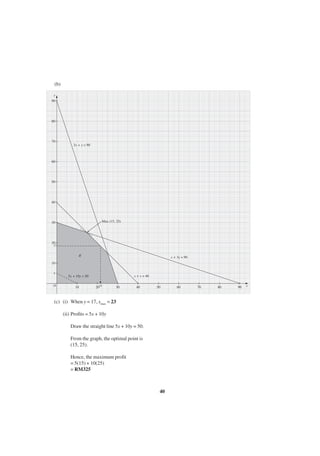
7. Paper 2
(b) g(x) = –2x2 + 8x – 12 = –2(x – 2)2 – 4
΂ 2 ϫ 5΃ = 4
(a) f(x) = 2x2 + 10x + k
k
= 2 x2 + 5x +
2
25
25 k
= 2 x2 + 5x +
–
+
4
4
2
5 2 25
k
=2 x+
–
+
2
4
2
2
5
25
=2 x+
–
+k
2
2
΂
΂
[΂
΂
΃
΃
1
2
25
The maximum point is (2, –4).
When x = 0, y = –12 ∴ (0, –12)
The graph of the function g(x) is as shown
below.
΃
y
]
O (2, –4)
΃
(b) (i) Minimum value = 32
25
–
+ k = 32
2
89
k =
2
(ii)
–12
3. y = h – 2x… 1
y2 + xy + 8 = 0 …
b2 – 4ac
2
10 – 4(2)(k)
100 – 8k
– 8k
<0
<0
<0
< –100
–100
k>
–8
25
k >
2
΂
(c) Minimum point is –2
2
Substituting 1 into 2 :
(h – 2x)2 + x(h – 2x) + 8 = 0
h2 – 4hx + 4x2 + hx – 2x2 + 8 = 0
2x2 – 3hx + h2 + 8 = 0
a = 2, b = –3h, c = h2 + 8
If a straight line does not meet a curve, then
b2 – 4ac < 0
2
(–3h) – 4(2) (h2 + 8) < 0
9h2 –8h2 – 64 < 0
h2 – 64 < 0
(h + 8)(h – 8) < 0
΃
1
, 32 .
2
2. (a) g(x) = –2x2 + px – 12 = –2(x + q)2 – 4
–2x2 + px – 12 = –2(x2 + 2qx + q2) – 4
= –2x2 – 4qx – 2q2 – 4
By comparison,
p = – 4q … 1 and –12
–2q2
q2
q
x
–8
= –2q2 – 4
= –8
=4
= ±2
8
h
Hence, the required range of values of h is
–8 < h < 8.
From 1 :
When q = 2, p = –4(2) = –8 (Not accepted)
When q = –2, p = –4(–2) = 8 (Accepted)
because p > 0 and q < 0)
7

8. SPM ZOOM–IN
Form 4: Chapter 4 Simultaneous Equations
Paper 2
1. 2x – 3y = 2
x2 – xy + y2 = 4
…
…
From 3 ,
When x = 0.70156, y = 2 – 4(0.70156)
= –0.80624
1
2
When x = –5.70156, y = 2 – 4(–5.70156)
= 24.80624
1
From
:
2 + 3y
x=
… 3
2
Substituting 3 into
2
Hence, the solutions are
x = 0.70156, y = –0.80624 or
x = –5.70156, y = 24.80624 (correct to five
decimal places).
:
΂ 2 +23y ΃ – y΂ 2 +23y ΃ + y – 4 = 0
2
2
(2 + 3y)2 – y(2 + 3y) + y2 – 4
4
2
(2 + 3y)2 – 2y(2 + 3y) + 4y2 – 16
4 + 12y + 9y2 – 4y – 6y2 + 4y2 – 16
7y2 + 8y – 12
(7y – 6)(y + 2)
3. (a) Since (16, m) is a point of intersection of
1
y = x – 2 and y2 + ky – x – 4 = 0, then
4
x = 16 and y = m satisfy both the equations.
=0
=0
=0
=0
=0
6
y=
or –2
7
From
3
When y = –2, x =
2+3
2
6
( 7 ) = 16
(b) When k = 8,
1
y= x–2…
4
7
2 + 3(–2)
= –2
2
΂
2 6
Hence, the points of intersection are 2 ,
7 7
and (–2, –2).
2. 4x + y = 2 … 1
x2 + x – y = 2 …
1
:
y = 2 – 4x…
2
=0
=0
= 16
=8
1
y2 + 8y – x – 4 = 0 …
΃
From 1 :
4y = x – 8
x = 4y + 8 …
3
,
2
3
Substituting 3 into
y2 + 8y – (4y + 8) – 4
y2 + 8y – 4y – 8 – 4
y2 + 4y – 12
(y – 2)(y + 6)
y
2
Substituting 3 into
x2 + x – (2 – 4x) = 2
x2 + 5x – 4 = 0
x = –5 ±
m2 + km – 16 – 4
22 + k(2) – 16 – 4
2k
k
:
6
When y = , x =
7
From
Therefore,
1
m = (16) – 2 = 2 and
4
2 ,
=0
=0
=0
=0
= 2 or –6
From 3 :
When y = 2, x = 4(2) + 8 = 16
When y = –6, x = 4(–6) + 8 = –16
52
– 4(1)(–4)
2(1)
= –5 ± 41
2
= 0.70156 or –5.70156
Hence, the other point of intersection,
other than (16, 2), is (–16, –6).
8

9. SPM ZOOM–IN
Form 4: Chapter 5 Indices and Logarithms
Paper 1
4.
5x
lg 5x
x lg 5
x lg 5
x lg 5 – 2x lg 3
x(lg 5 – 2lg 3)
5.
log10 (p + 3)
log10 (p + 3) – log10 p
log10 p + 3
p
p+3
p
p+3
9p
1. 2 x + 3 + 2x + 16 (2x – 1)
2x
= 2x.23 + 2x + 16
2
= 8(2x) + 2x + 8(2x)
= (8 + 1 + 8)( 2x)
= 17(2x)
΂ ΃
2.
3x + 3 – 3x + 2
3 (33) – 3x (32)
27(3x) – 9(3x)
(27 – 9)(3x)
18(3x)
x
3x
3x
3x
x
3.
m = 3a
log3 m = a
΂
=6
=6
=6
=6
=6
= 6
18
= 1
3
= 3–1
= –1
= 32x – 1
= lg 32x –1
= (2x – 1) lg 3
= 2x lg 3 – lg 3
= – lg 3
= –lg 3
–lg 3
x =
lg 5 – 2 lg 3
x = 1.87
΂
= 1 + log10 p
=1
΃ =1
= 101
= 10p
=3
1
p =
3
n = 3b
log3 n = b
6.
΃
mn4
log3
27
= log3 m + log3 n4 – log3 27
= log3 m + 4 log3 n – log3 33
= a + 4b – 3
log2 y – log8 x
log2 x
log2 y –
log2 8
log2 x
log2 y –
3
3 log2 y – log2 x
log2 y3 – log2 x
y3
log2
x
y3
x
y3
=1
=1
=1
=3
=3
΂ ΃ =3
= 23
= 8x
y3
x =
8
9
log2 8 = log2 23 = 3

10. SPM ZOOM–IN
Form 4: Chapter 6 Coordinate Geometry
Hence, the area of ∆PQR
1 4 0 2 4
=
2 0 –3 5 0
1 |–12 – (–6 + 20)|
=
2
= 1 |–26|
2
= 1 ϫ 26
2
= 13 units2
Paper 1
1. Let point A be (0, k).
AB = 10
2 + (k – 7)2 = 10
(0 – 8)
64 + k2 – 14k + 49 = 102
k2 – 14k + 13 = 0
(k – 1)(k – 13) = 0
k = 1 or 13
Based on the diagram, k < 7.
∴k=1
∴ A(0, 1)
4. (a) 2y = 3x – 12
At point L (on the x-axis), y = 0
2(0) = 3x – 12
x =4
∴ L (4, 0)
2. (a) x + 2y + 6 = 0
x + 2y = –6
x
2y
–6
+
=
(–6) (–6) –6
x
y
+
=1
(–6) (–3)
΂ ΃
(b) mMN = – –3 = – 1
–6
2
At point N (on the y-axis), x = 0.
2y = 3(0) – 12
y = –6
∴ N (0, –6)
Intercept form:
x y
+ =1
a b
΂
΃
∴ M = 4 + 0 , 0 + (–6) = (2, –3)
2
2
m = – y-intercept
x-intercept
(b) mLN = –6 – 0 = 3
0–4
2
Therefore, the gradient of the perpendicular
line is 2.
∴ Gradient of perpendicular line = – 2
3
Hence, the equation of the straight line which
passes through the point N and is
perpendicular to the straight line MN is
y = 2x – 3.
Hence, the equation of the perpendicular
line is
y – y1 = m(x – x1)
y – (–3) = – 2 (x – 2)
3
3(y + 3) = –2(x – 2)
3y + 9 = –2x + 4
3y = –2x – 5
y
3. x – = 1
4 3
At point P (on the x-axis), y = 0.
x – 0 =1⇒x=4
4 3
∴ P is point (4, 0).
5.
PA
(x –
+ (y – 2)2
2
(x – 1) + (y – 2)2
2
x – 2x + 1 + y2 – 4y + 4
–2x – 4y + 5
–2x + 2y – 4
–x + y – 2
y
At point Q (on the y-axis), x = 0.
0 – y = 1 ⇒ y = –3
4 3
∴ Q is point (0, –3).
1)2
10
= PB
= (x – 0)2 + (y – 3)2
= (x – 0)2 + (y – 3)2
= x2 + y2 – 6y + 9
= –6y + 9
=0
=0
=x+2

11. Paper 2
(c) A(–18, 0), B(2, 0), C(0, –6), D(–20, –6)
Area of ABCD
1 –18 2 0 –20 –18
=
2
0 0 –6 –6 0
1 |–12 – (120 + 108)|
=
2
= 1 ϫ 240
2
= 120 units2
1. (a) y – 3x + 6 = 0
At point B (x-axis), y = 0.
0 – 3x + 6 = 0 ⇒ x = 2
∴ B is point (2, 0).
y – 3x + 6 = 0
At point C (y-axis), x = 0.
y – 3(0) + 6 = 0 ⇒ y = –6
∴ C is point (0, –6).
2. (a) (i) y – 3x + 6 = 0
At point P (on the y-axis), x = 0.
y – 3(0) + 6 = 0 ⇒ y = –6
∴ P is point (0, –6).
(ii) The coordinates of point S are
4(0) + 3(7) , 4(–6) + 3(15) = (3, 3)
3+4
3+4
y = 3x – 6
mBC = 3
∴mAC = – 1
3
΂
Let A(k, 0).
∴ mAC = – 1
3
0 – (–6) = – 1
k–0
3
–k = 18
k = –18
∴ A is point (–18, 0).
(b) Let D (p, q).
Midpoint of BD = Midpoint of AC
2 + p , 0 + q = –18 + 0 , 0 + (–6)
2
2
2
2
΂
΃ ΂
΂ 2 + p , q ΃ = (–9, –3)
2
2
΃
(b) Area of ∆QRS = 48 units2
1 k
7 3 k = 48
2 0 15 3 0
15k + 21 – (45 + 3k) = 96
12k – 24 = 96
12k = 120
k = 10
(c) S(3, 3), Q(10, 0), T(x, y)
TS : TQ = 2 : 3
TS = 2
TQ 3
3TS = 2TQ
9(TS)2 = 4(TQ)2
9[(x – 3)2 + (y – 3)2] = 4[(x – 10)2 + (y – 0)2]
9(x2 – 6x + 9 + y2 – 6y + 9) =
4(x2 – 20x + 100 + y2)
2
2
9x – 54x + 81 + 9y – 54y + 81 =
4x2 – 80x + 400 + 4y2
2
2
5x + 26x + 5y – 54y – 238 = 0
΃
Equating the x-coordinates,
2 + p = –9
2
p = –20
Equating the y-coordinates,
q = –3
2
q = –6
∴ D is point (–20, –6).
11

12. SPM ZOOM–IN
Form 4: Chapter 7 Statistics
Paper 1
␴2 =
1. After the given score are arranged in
ascending order, we have
6
6
6
k
k
=
9
Since the mode is 6, then k ≠ 9.
6
6
8
8
4.
2
Number
1
k
6
2
2
1
(a) 1 < k < 6
k = 2, 3, 4, 5
After two new scores, 7 and 10, are added to the
original scores, the mean of the eight scores
= 6 + 6 + 6 + 8 + 8 + 9 + 7 + 10
8
= 7.5
(b)
΂ ΃
10 132
318
–
10
10
Frequency
9
Median = 7
2. (a)
2
= 1.96
For 7 to be the median, k = 8, as shown below.
6
΂ ΃
∑fx 2
∑fx
–
∑f
∑f
k + 3 11
3
1
13
1
6 < k + 3 < 11
3<k<8
k = 4, 5, 6, 7
Taking into consideration both cases,
k = 4 or 5
(b) 1, 1, 4, 4, 6,
– ∑x
x =
n
189
27 =
n
189
n=
27
n =7
7, 7, 7, 11, 13
M
Q3
∴ Q3 = 7
Paper 2
1.
Mass (kg)
␴=
1.1 – 2.0
2.1 – 3.0
3.1 – 4.0
4.1 – 5.0
5.1 – 6.0
∑x 2
_
— – ( x )2
—
n
=
Frequency
5278
— — – 27 2
—
7
= 25
= 5
(a)
5
9
12
8
6
Cumulative
frequency
5
14
26
34
40
Frequency
12
3.
x
30
32
34
Sum
f
3
5
2
10
fx
90
160
68
318
fx2
2700
5120
2312
10 132
10
8
6
4
2
0
1.05
2.05
Mode = 3.5 kg
12
3.05 4.05 5.05
3.5 (Mode)
6.05
Mass (kg)

13. (b) The Q1 class is given by
(a)
Median = 46.5
΄ ΅
n –F
2
c = 46.5
L+
fm
T 40 = T 10 = 2.1 – 3.0
4
Q1 = 2.05 +
΄
40 – 5
4
(1) = 2.61 kg
9
΅
΄
The Q3 class is given by
΄
T 3 (40) = T 30 = 4.1 – 5.0
4
Q3 = 4.05 +
΄
΅
26 + k– –11
2
(10) = 46.5
39.5 +
k
΅
3
(40) – 26
4
(1) = 4.55 kg
8
΅
26 + k– –11
2
(10) = 7
k
26 + k – 11 = 0.7k
2
26 + k – 22 = 1.4k
Hence, the interquartile range
= Q3 – Q1 = 4.55 – 2.61 = 1.94 kg
0.4k = 4
k = 10
(c) New interquartile range
= Original interquartile range
= 1.94 kg
(b)
Marks
2.
Marks
f
20 – 29
30 – 39
40 – 49
50 – 59
60 – 69
70 – 79
4
7
k
8
5
2
20 – 29
30 – 39
40 – 49
50 – 59
60 – 69
70 – 79
Cumulative
frequency
4
11
11 + k
19 + k
24 + k
26 + k
f
4
7
10
8
5
2
36
Midpoint (x)
24.5
34.5
44.5
54.5
64.5
74.5
Variance =
=
fx
fx2
98.0
241.5
445.0
436.0
322.5
149.0
1692
2401.00
8331.75
19802.50
23762.00
20801.25
11100.50
86199
΂ ΃
∑fx 2
∑fx
–
∑f
∑f
΂
2
86 199
1692
–
36
36
΃
2
= 185.42
(c) (i) New median = Original median + 10
= 46.5 + 10
= 56.5
(ii) New variance = Original variance
= 185.42
13

14. SPM ZOOM–IN
Form 4: Chapter 8 Circular Measure
Paper 1
1.
2. ∠BOC = 20º = 20 ϫ 3.142 rad
180
΂
B
C
OB =
π – 1.8
A
0.9 rad
8 cm
O
0.9 rad
8 cm
΃
15.36
= 44 cm
20 ϫ 3.142
180
(
)
D
r=
∠BOC = π – ∠AOB – ∠COD
= 3.142 – 0.9 – 0.9
= 1.342 rad.
s
θ
3. Area of the shaded region
= Area of sector OAB – Area of sector OXY
= 1 ϫ 82 ϫ 1.2 – 1 ϫ 5 ϫ 4
2
2
1 2
rθ
2
= 38.4 – 10
= 28.4 cm2
14
·
·
Area of sector BOC
= 1 ϫ 82 ϫ 1.342
2
= 42.94
1
rs
2

15. Paper 2
(c) Perimeter of the shaded region
1.
= 2r sin θ + rθ
2
C
΂
= 2(10) sin 1.982
2
= 16.73 + 19.82
= 36.55 cm
6 cm
8 cm
8 cm
M
΃ + 10(1.982)
r
B
A
(r – 6) cm
3.
r cm
D
4c
O
m
(a) MO = r – 6
In ∆OMB, using Pythagoras’ theorem,
MO2 + MB2 = OB2
(r – 6)2 + 82 = r2
MB =
C
4c
m
3 cm
1
1
AB = ϫ 16 = 8 cm
2
2
5 cm
r =8 1
3
In ∆ADB,
cos ∠ABD = 8
10
∠ABD = 0.6435 rad
(b) In ∆BOM,
8
81
3
(b) ∠AOD = 2 ϫ ∠ABD
= 2 ϫ 0.6435
= 1.2870 rad
sin ∠BOM = 24
25
∠BOM = 1.287 rad.
∴ ∠AOB = 2 ϫ 1.287 = 2.574 rad.
The angle at the centre
is twice the angle at
circumference.
∴ Length of the arc AD
= 5 ϫ 1.2870
= 6.435 cm
(c) Area of the shaded region
2
=1 ϫ 81
2.574 – sin 2.574r
2
3
= 70.71 cm2
΂ ΃΂
5 cm
(a) Since ∆ADB is inscribed in a semicircle,
it is a right-angled triangle.
r2 – 12r + 36 + 64 – r2 = 0
–12r + 100 = 0
sin ∠BOM =
B
O
A
(c) Area of ∆ODB
= 1 ϫ8ϫ3
2
= 12 cm2
΃
2. (a) ∠BOA = π – 0.822 = 1.160 rad.
2
∴ ∠BOQ = π – 1.160 = 1.982 rad.
Area of sector BOC
= 1 ϫ 52 ϫ 0.6435
2
= 8.04375 cm2
(b) Area of the shaded region
= 1 r 2 (θ – sin θ)
2
= 1 (10)2 (1.982 – sin 1.982 r )
2
= 53.27 cm2
Hence, the area of the shaded region
= Area of ∆ODB – Area of sector BOC
= 12 – 8.04375
= 3.956 cm2
15

16. SPM ZOOM–IN
Form 4: Chapter 9 Differentiation
Paper 1
4. z = xy
z = x(30 – x)
z = 30x – x2
dz = 30 – 2x
dx
1
= (5x – k)–2
(5x – k)2
f ′(x) = –2(5x – k)–3 (5)
= –10 3
(5x – k)
1. f (x) =
f ′(1)
–10
[5(1) – k]3
(5 – k)3
5–k
k
2.
= 10
= 10
= –1
=–1
=6
d 2z = –2 (negative)
dx2
Hence, the maximum value of z
= 30(15) – 152
= 225
y = (x + 1) (2x – 1)2
dy = (x + 1) 2 (2x – 1)1 (2) + (2x – 1)2 (1)
dx
= (2x – 1)[4(x + 1) + (2x – 1)]
= (2x – 1)(6x + 3)
[
3.
When z has a stationary value,
dz = 0
dx
30 – 2x = 0
x = 15
]
5.
y=
1
= (2x – 5)–3
(2x – 5)3
dy = –3 (2x – 5)–4 (2) = – 6
dx
(2x – 5)4
3
y = 2x – 4x + 5
dy = 6x2 – 4
dx
δy ≈ dy
δx dx
δy ≈ dy ϫ δy
dx
= – 6 4 ϫ (3.01 – 3)
(2x – 5)
–6
=
ϫ 0.01
[2(3) – 5]4
= – 0.06
Gradient at the point (–1, 7)
= 6 (–1)2 – 4
=2
Equation of the tangent is
y – 7 = 2[x – (–1)]
y – 7 = 2(x + 1)
y – 7 = 2x + 2
y = 2x + 9
6. A = 2πr 2 + 2πrh
= 2πr 2 + 2πr(3r)
= 8πr 2
dA = dA ϫ dr
dt
dt
dr
= 16πr ϫ 0.1
= 16π (5) ϫ 0.1
= 8π cm2 s–1
16

17. Paper 2
1.
(b) When p = –3 and k = 4,
y = –3x3 + 4x
dy = –9x 2 + 4
dx
d 2 y = –18x
dx2
y = 12 – 13 = x–2 – x–3
x
x
dy = –2x – 3 + 3x – 4 = – 2 + 3
dx
x3 x4
2
d y = 6x– 4 – 12x– 5 = 6 – 12
x4 x5
dx2
At turning points,
dy = 0
dx
–9x2 + 4 = 0
x2 = 4
9
x =± 2
3
΂
΃
x ΂ – 2 + 3 + 6 – 12 ΃ +
x
x
x
x
x4 dy + d y + x 2y + 5 = 0
dx dx 2
2
4
3
4
4
5
x2
΂ x1 – x1 ΃ + 5 = 0
2
3
–2x + 3 + 6 – 12 + 1 – 1 + 5 = 0
x
x
–2x + 15 – 13 = 0
x
2
–2x + 15x – 13 = 0
2x2 – 15x + 13 = 0
(2x – 13)(x – 1) = 0
x = 13 or 1
2
When x = 2 ,
3
΂ ΃ + 4΂ 2 ΃ = 1 7
3
9
d y = – 18 2 = –12 (< 0)
΂ 3΃
dx
∴ ΂ 2 , 1 7 ΃ is a turning point which is
3 9
y = –3 2
3
2
2
2. (a) y = px3 + kx
dy = 3px2 + k
dx
a maximum.
When x = – 2 ,
3
At (1, 1), x = 1 and m = dy = –5.
dx
∴ 3px2 + k = –5
3p(1)2 + k = –5
3p + k = –5 … 1
΂ ΃ + 4΂– 2 ΃ = –1 7
9
3
d y = –18 – 2 = 12 (> 0)
΂ 3΃
dx
∴ ΂ – 2 , –1 7 ΃ is a turning point which is
3
9
y = –3 – 2
3
–
2
2
2
a minimum.
: 2p = –6 ⇒ p = –3
From
3
2
The curve passes through point (1, 1).
∴ 1 = p(1)3 + k(1)
p+k=1… 2
: –3 + k = 1 ⇒ k = 4
1
3
17

18. 3.
(b)
V
4x m
5x m
H
E
F
G
D
3x m y m
At stationary point,
dL = 0
dx
3888 = 0
192x –
x2
192 x = 3888
x2
x 3 = 3888
192
C
6x m
A
6x m
L = 96x2 + 3888 = 96x2 + 3888x–1
x
dL = 192x – 3888x–2 = 192x – 3888
dx
x2
B
(a) Volume of the cuboid = 5832 cm3
(6x)(6x)(y) = 5832
36x2y = 5832
x2y = 162
y = 162
x2
x 3 = 20.25
x = 2.73
L = Area of ABCD + 4 (Area of GBCH)
+ 4 (Area of VGH)
L = (6x)2 + 4(6xy) + 4 ϫ 1 (6x)(5x)
2
L = 36x2 + 24xy + 60x2
L = 96x2 + 24xy
L = 96x2 + 24x 162
x2
L = 96x2 + 3888 (shown)
x
d 2L = 192 + 7776x–3 = 192 + 7776 (> 0)
x3
dx 2
∴ L is a minimum.
4.
΂ ΃
y=
h
= h(1 + 2x)–2
(1 + 2x)2
dy = –2h(1 + 2x)–3 (2) = – 4h
dx
(1 + 2x)3
δy = dy ϫ δx
dx
8c = – 4h
–
ϫc
3
(1 + 2x)3
4h
– 8c = –
ϫc
3
[1 + 2(1)]3
– 8c = – 4hc
3
27
h = 8 ϫ 27
3
4
h = 18
18

19. SPM ZOOM–IN
Form 4: Chapter 10 Solution of Triangles
2. (a) In ∆PQS, using the sine rule,
sin ∠QSP = sin 35º
8
7
sin ∠QSP = sin 35º ϫ 8
7
sin ∠QSP = 0.65552
∠QSP = 40.96º
Paper 2
1. (a) ∠UST = 180º – 65º = 115º
∠SUT = 180º – 43º – 115º = 22º
In ∆UST, using the sine rule,
US = 9
sin 43º sin 22º
US = 9 ϫ sin 43º
sin 22º
= 16.385 cm
∴ ∠PQS = 180º – 35º – 40.96º
= 104.04º
Hence, the area of ∆PQS
= 1 ϫ 8 ϫ 7 ϫ sin 104.04º
2
U
22°
= 27.16 cm2
16
(b) This problem involves the ambiguous case of
sine rule. The sketch of ∆QRS1 is as shown
below.
.3
85
cm
Q
115°
65°
R
43°
S
7 cm
9 cm
T
10 cm
(b) In ∆USR, using the cosine rule,
UR2 = 72 + 16.3852 – 2(7)(16.385)cos 65º
UR2 = 220.5238
UR = 14.85 cm
1 ϫ 7 ϫ 12 ϫ sin ∠RSV
2
sin ∠RSV
Basic ∠
∠RSV
R
7 cm
7 cm
43°
R
S1
S
In ∆QRS, using the sine rule,
sin ∠QSR = sin 43º
10
7
sin 43º ϫ 10
sin ∠QSR =
7
Area of ∆RSV = 41.36 cm2
(c)
7 cm
= 41.36
= 0.98476
= 79.98º
= 180º– 79.98º
= 100.02º
sin ∠QSR = 0.974283
Basic ∠ = 76.98º
∴ ∠QSR = 76.98º or ∠QS1R = 103.02º
S
100.02°
In ∆QS1R,
∠RQS1 = 180º – 43º – 103.02º = 33.98º
12 cm
In ∆QS1R, using the sine rule,
RS1
10
=
sin ∠RQS1
sin ∠RS1Q
RS1
10
=
sin 33.98º
sin 103.02º
10
RS1 =
ϫ sin 33.98º
sin 103.02º
= 5.737 cm
V
In ∆RSV, using the cosine rule,
RV 2 = 72 + 122 – 2(7)(12)cos 100.02º
RV 2 = 222.23064
RV = 14.91 cm
19

20. SPM ZOOM–IN
Form 4: Chapter 11 Index Numbers
Paper 2
1. (a)
(a) Supplement A
x ϫ 100 = 120
400
x = 480
I2004 (based on 2002) = 115
P2004
ϫ 100 = 115
P2002
69
ϫ 100 = 115
P2002
P2002 = 69 ϫ 100
115
P2002 = RM60.00
P2004
I= P
ϫ 100
2002
y = 525 ϫ 100 = 105
500
660 ϫ 100 = 110
z
z = 600
(b) Supplement B
I2006 (based on 2002)
P
= 2006 ϫ 100
P2002
P
P
= 2006 ϫ 2004 ϫ 100
P2004
P2002
= 130 ϫ 120 ϫ 100
100 100
= 156
–
(b)
I = 115
(120 ϫ 20) + 130m + (105 ϫ 80) + (110 ϫ 40) = 115
20 + m + 80 + 40
15 200 + 130m = 115
140 + m
15 200 + 130m = 16 100 + 115m
15m = 900
m = 60
(c)
–
(c) I 2006 (based on 2002)
–
= 100 + 25 ϫ I 2004
100
= 125 ϫ 115
100
= 143.75
(115 ϫ 3) + (120 ϫ 2) + 105x
3+2+x
585 + 105x
5+x
585 + 105x
30
x
–
(d) I 2006 (based on 2004)
(d) Total yearly cost in 2006
= 143.75 ϫ 5 500 000
100
= RM7 906 250
= 111
= 111
= 555 + 111x
= 6x
=5
= (150 ϫ 3) + (130 ϫ 2) + (120 ϫ 5)
3+2+5
= 1310
10
= 131
P
Thus, 2006 ϫ 100 = 131
P2004
P2006
ϫ 100 = 131
300
P2006 = 131 ϫ 300
100
P2006 = RM393
2.
Health
I2004 (based
supplement on 2002)
A
115
B
120
C
105
–
I 2004 (based on 2002) = 111
I2006 (based
Weightage
on 2004)
150
3
130
2
120
x
20

21. SPM ZOOM–IN
Form 5: Chapter 1 Progressions
4.
Paper 1
1. (a)
T6 = 38
a + 5d = 38
a + 5(7) = 38
a =3
r = – 1 or 3
2
2
(b) S9 – S3
= 9 [2(3) + 8(7)] – 3 [2(3) + 2(7)]
2
2
= 279 – 30
= 249
2. (a)
T2 – T1
2h – 1 – (h – 2)
h+1
h
5. 0.242424 …
= 0.24 + 0.0024 + 0.000024 + …
a
= 0.24
S∞ =
1 – 0.01
1–r
= 0.24
0.99
= 24
99
= 8
33
= T3 – T2
= 4h – 7 – (2h – 1)
= 2h – 6
=7
(b) When h = 7, the arithmetic progression is 5,
13, 21, … with a = 5 and d = 8.
6. The numbers of bacteria form a geometric
progression 3, 6, 12, …
S8 – S3
= 8 [2(5) + 7(8)] – 3 [2(5) + 2(8)]
2
2
= 264 – 39
= 225
3.
T3 – T2 = 3
ar 2 – ar = 3
4r 2 – 4r = 3
2
4r – 4r – 3 = 0
(2r + 1)(2r – 3) = 0
The number of bacteria after 50 seconds
= T11 = ar10 = 3(210) = 3072
Paper 2
1. (a) The volumes of cylinders are
πr 2h, πr 2 (h + 1), πr 2 (h + 2), …
T2 T3
=
T1 T2
x+2 = x–4
9x + 4
x+2
(x
= (x – 4)(9x + 4)
x2 + 4x + 4 = 9x2 – 32x – 16
2
8x – 36x – 20 = 0
2x2 – 9x – 5 = 0
(2x + 1)(x – 5) = 0
x = – 1 or 5
2
T2 – T1 = πr 2 (h + 1) – πr 2h
= πr 2h + πr 2 – πr 2h
= πr2
T3 – T2 = πr 2 (h + 2) – πr 2 (h + 1)
= πr 2h + 2πr 2 – πr 2h – πr 2
= πr2
Since T2 – T1 = T3 – T2 = πr 2, the
volumes of cylinders form an arithmetic
progression with a common difference of πr2.
21

22. 2. (a)
(b) a = πr 2h, d = πr 2
T4 = 32π
a + 3d = 32π
πr 2h + 3πr 2 = 32π
r 2h + 3r 2 = 32
r 2 (h + 3) = 32 …
2
1
1
2
: a (1 + r) = 150
45
ar (r – 1)
1 + r = 10
r (r – 1)
3
1
2
2
3 + 3r = 10r2 – 10r
10r – 13r – 3 = 0
(2r – 3)(5r + 1) = 0
r = 3 or – 1
2
5
2
2
: r 2(2h + 3) = 52
32
r (h + 3)
2h + 3 = 13
h+3
8
16h + 24 = 13h + 39
3h = 15
h =5
From 1
r 2 (5 + 3)
r2
r
= 150
= 150
= 150
= 150 …
T3 – T2 = 45
ar 2 – ar = 45
ar (r – 1) = 45 …
1
S4 = 104π
4 (2a + 3d) = 104π
2
4a + 6d = 104π
4πr 2h + 6πr 2 = 104π
2r 2h + 3r 2 = 52
r 2 (2h + 3) = 52 …
S2
T1 + T2
a + ar
a (1 + r)
(b) For the sum to infinity to exist, – 1 < r < 1.
Thus, r = 3 is not accepted.
2
Therefore, r = – 1
5
:
= 32
=4
=2
From
1
:
1 = 150
a 1–
5
΂
΃
a = 187 1
2
1
187
a
2
∴ S∞ =
=
1–r 1– –1
5
΂ ΃
22
= 156 1
4

23. SPM ZOOM–IN
Form 5: Chapter 2 Linear Law
Paper 2
Paper 1
y = 2 + qx
x
y = 2 +q
x x2
y =2( 1 )+q
x
x2
1.
1
x2
1. (a)
y = hxk
log10 y = log10 (hxk)
1
log10 y 2 = log10 h + log10 xk
1 log y = log h + klog x
10
10
2 10
log10 y = 2log10 h + 2klog10 x
y
x
log10 y = 2k log10 x + 2 log10 h
5 = 2(1) + q
q=3
(1, 5)
(b)
1
x2
q=3
y
x
(3, p)
2.
y
k
lg
x
x
lg y – lg k
p = 2(3) + 3
p=9
1.5
142
0.18
2.15
2.0
338
0.30
2.53
2.5
660
0.40
2.82
3.0
1348
0.48
3.13
3.5
1995
0.54
3.30
The graph of log10 y against log10 x is as
shown below.
=p
= lg p
y
k
x
y
log 10 x
log 10 y
x
log10 y
= lg p
Graph of log10 y against log10 x
3.5
lg y – x lg k = lg p
3.0
lg y = x lg k + lg p
∴ Y = lg y, X = x, m = lg k, c = lg p
2.0
2
3. y – ax = b2
x
x
2
3
xy – ax = b
xy2 = ax3 + b
1.0
0.5
O
x3
1
xy2
–
2
:
12 = –6a
a = –2
From
2
:
0.55 – 0.06 = 0.49
1.55 1.5
10 = a(–1) + b … 1
–2 = a(5) + b … 2
(–1, 10):
(5, –2):
3.35 – 1.75
= 1.6
2.5
–2 = –2(5) + b
b =8
23
0.1
0.2
0.3
0.4
0.5
0.6
log10 x

24. (c) 2k = Gradient
2k = 3.35 – 1.75
0.55 – 0.06
2k = 3.2653
k = 1.63
2 log10 h
2 log10 h
log10 h
h
(b) (i) 1
=
y
1 = x+p
y2
q
1 = 1x+ p
y2 q
q
= Y–intercept
= 1.55
= 0.775
= 5.96
Gradient =
x
y
0.1 0.3
0.78 0.60
0.4
0.54
0.5
0.50
0.7
0.44
0.8
0.42
1
y2
1.64 2.78
3.43
4.00
5.17
5.67
Graph of
Y-intercept
p
q
p
0.17
p
1
against x
y2
4.6 – 2
0.6 – 0.16
= 1.1
= 1.1
= 1.1
= 0.19
(ii) When x = 0.6, from the graph,
1 = 4.6
y2
y2 = 0.2174
y = 0.47
5.0
4.6 4.5
4.0
3.5
4.6 – 2 = 2.6
3.0
2.5
2.0
0.6 – 0.16 = 0.44
1.5
1.1 1.0
0.5
O
Squaring both sides.
1 = 5.91
q
q = 0.17
2. (a)
1
y2
5.5
x+p
q
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
x
24

25. SPM ZOOM–IN
Form 5: Chapter 3 Integration
4. Area of the shaded region
Paper 1
(y – 5) dy = 8
5
k
]
[
΂
2
2
=
k
1.
΃
2
=
=
–1
y2 –5y = 8
5
2
2
k – 5k – 5 – 5(5) = 8
2
2
2
k – 5k + 25 = 8
2
2
k2 – 10k + 25
= 16
k2 – 10k + 9 = 0
(k – 1)(k – 9) = 0
k = 1 or 9
–1
y dx
(x2 – 2x + 1) dx
2
[ x3 – x + x]
3
2
–1
΂
΃
= 8 – 4 + 2 – – 1 –1 – 1
3
3
= 3 units2
Paper 2
y
1.
y = –x3 – x
2.
2
–1
4
3g (x) dx +
[
= 3[
=3
2
–1
4
–1
2
3g (x) dx
4
g(x) dx +
2
]
g(x) dx
1O
]
g(x) dx
x
2
P
Q
= 3(20)
= 60
3. dy = x4 – 8x3 + 6x2
dx
y=
΂
4
3
Area P
0
x – 8x + 6x
5
΃
2
–1
dx
0
=
΂ ΃ ΂ ΃+c
4
y dx
3
y = x –8 x +6 x
5
4
3
5
4
3
y = x – 2x + 2x + c
5
–1
(–x3 –x) dx
0
[
]
4
2
= – x – x
4
2 –1
(–1)4 – (–1)2
=0– –
4
2
= 1 + 1
4
2
= 3
4
[
Since the curve passes through the point
΂1, – 1 4 ΃,
5
– 9 = 1 –2 + 2 + c
5
5
c = –2
Area Q
Hence, the equation of the curve is
5
y = x – 2x4 + 2x3 – 2.
5
=
2
0
y dx
2
0
[
(–x3 – x) dx
2
]
4
2
= – x – x
4
2 0
24 – 22 – 0
=–
4
2
= –4 – 2
= –6
25
]

26. Hence, the total area of the shaded region
= Area P + |Area Q|
= 3 + |–6|
4
= 6 3 units2
4
2. (a)
(b) When h = 1 and k = 4, y = x2 + 4
y
y = x2 + 4
P
y = hx2 + k
dy = 2hx
dx
x =3
4
At the point (–2, 8), the gradient of the
curve is – 4.
∴ dy = – 4
dx
2hx = – 4
2h (–2) = – 4
– 4h = – 4
h =1
x
O
2
3
Q
Volume generated, Vx
= Volume generated by the curve –
Volume generated by the straight line PQ
(from x = 0 to x = 2)
3
= π 0 y2 dx – 1 πr2h
3
3
2
2
= π 0 (x + 4) dx – 1 π(4)2 (2)
3
3
4
2
= π 0 (x + 8x + 16) dx – 32 π
3
3
5
3
32 π
= π x + 8x + 16x –
0
3
5
3
5
= π 3 + 8 (3)3 + 16(3) – 0] – 32 π
3
3
5
14 π units3
= 157
15
The curve y = hx2 + k passes through the
point (–2, 8).
∴ 8 = h(–2)2 + k
8 = 4h + k
8 = 4(1) + k
k =4
[
[
26
]

27. SPM ZOOM–IN
Form 5: Chapter 4 Vectors
Paper 1
4. (a) If the vectors _ and _ are parallel, then
a
b
→
→
1. (a) EA = 3 DC = 3 (12p) = 9p
_
_
4
4
a = hb (h is a constant).
_ _
2i – 5j = h(ki – 3j)
_ _
_ _
2i – 5j = hki – 3hj
_ _
_
_
→
→
(b) EQ = 1 ED
2
→ → → →
= 1 EA + AB + BC + CD
2
Equating the coefficients of _
j
–3h = –5
h= 5
3
΂
΃
= 1 ΂ 9p – 6r – 9q – 12p΃
_ _
_
2 _
= 1 ΂ – 3p – 6r – 9q ΃
_ _ _
2
Equating the coefficients of _
i
hk = 2
5 k =2
3
k= 6
5
→
→ →
2. XY = XD + DY
→
→
= 1 BD + 2 DC
2
3
→ →
→
= 1 BA + AD + 2 AB
2
3
(b)
΂
΃
= 1 ΂ –6b + 2a΃ + 2 (6b)
_ _
2
3 _
|a| 5
|b| = 3
|a| : |b| = 5 : 3
= –3b + _ + 4b
_ a _
=_ +_
a b
→ → →
5. (a) AC = AB + BC
= 9i – 4j + (–6i + mj )
_ _
_
_
3. (a) _ + 1 _ + 2c
a
b _
5
= 7j + 1 (10i – 5j ) + 2(–4i +_ )
_ _
_ j
_ 5
= 7j + 2i – _ – 8i + 2j
_ _ j _ _
= 3i + (m – 4)_
_
j
→
(b) If AC is parallel to the x-axis, the
coefficient of _ equals zero.
j
m–4 =0
m =4
= – 6i + 8j
_ _
(b) |a + 1 _ + 2c | = (–6)2 + 82 = 10
b _
_
5
Hence, the unit vector in the direction of
a 1b _
_ + _ + 2c
5
΂
= 1 –6i + 8j
_ _
10
a
_ = hb
_
5
a
_ = b
_
3
΃
= – 3_ + 4_
i
j
5
5
27

28. Paper 2
(c) Since the points O, T and S are collinear,
→
→
then, OT = kOS , where k is a constant.
→ → →
1. (a) OT = OA + AT
→
= 4x + 1 AQ
_
3
→ →
= 4x + 1 (AO + OQ )
_
3
= 4x + 1 (–4x + 6y)
_
_ _
3
= 8 _ + 2y
x _
3
→
→
OT = kOS
8 _ + 2y = k [(6 – 6h)y + 16hx
x _
_]
_
3
8 _ + 2y = k (6 – 6h)y + 16hkx
x _
_
_
3
8 _ + 2y = (6k – 6hk)y + 16hkx
x _
_
_
3
→
→ →
(b) OS = OQ + QS
→
= 6y + hQP
_
→ →
= 6y + h(QO + OP )
_
→
→
= 6y + h(QO + 4OA )
_
Equating the coefficients of _,
x
8 = 16hk
3
1 = 6hk
hk = 1 … 1
6
= 6y + h[–6y + 4(4x
_)]
_
_
Equating the coefficients of _,
y
6k – 6hk = 2 … 2
= (6 – 6h) _ + 16hx
y
_
Substituting
1
into
΂ ΃
6k – 6 1 = 2
6
6k = 3
k= 1
2
From
2
:
hk = 1
6
΂ ΃
h 1 =1
2
6
h= 1
3
28
2
:

29. →
→
2. (a) (i) OM = 5 OB = 5 (14y) = 10y
_
_
7
7
→ → →
(c) AK = AL + LK
΂
_
_
– 1 _ + 7 _ = –2px + 10py + 3 qx + 7 qy
x
y
_
_
2
2
2
2
→
→
(ii) AK = 1 AB
4
→
→
= 1 AO + OB
4
΂
–x + 7y = (–4p + 3q)x + (20p + 7q)y
_ _
_
_
Equating the coefficients of _ ,
x
– 4p + 3q = –1 … 1
=– 1 _ + 7_
x
y
2
2
Equating the coefficients of _ ,
y
20p + 7q = 7 … 2
→
→
(b) (i) AL = pAM
→
→
= p AO + OM
΃
+
= p(–2x + 10y)
_
_
= –2px + 10py
_
→
→
(ii) KL = qKO
→ →
= q KA + AO
΃
·
΂
΃
– 1 _ + 7 _ = –2p + 3 q _ + 10p + 7 q _
x
y
x
y
2
2
2
2
΂
΃
= 1 ΂ –2x + 14y΃
_
_
4
΂
΃ ΂
΃
–20p + 15q = –5 …
20p + 7q= 7 …
22q = 2
q= 1
11
From
1
2
1
:
– 4p + 3 1 = –1
11
΂ ΃
→
→
KA = –AK
= 1_ – 7_
x
y
2
2
– 4p = – 14
11
7
p=
22
΂
΃
= q΂ – 3 _ – 7 _΃
x
y
2
2
= q 1 _ – 7 _ – 2x
x
y _
2
2
= – 3 qx – 7 qy
_
2
2 _
29
ϫ5

30. WebsiteZI F505_4th pp
10/15/08
9:40 AM
Page 30
SPM ZOOM–IN
Form 5: Chapter 5 Trigonometric Functions
Paper 1
3.
3 tan θ = 2 tan (45º – θ)
3 tan θ = 2
45º –
΂ 1tantan 45ºtan θθ ΃
+
tan
3 tan θ = 2
1.
– tan
΂ 11 + tan θθ ΃
1 + p2
θ
1
O
–p
3 tan θ + 3 tan2 θ = 2 – 2 tan θ
3 tan2 θ + 5 tan θ – 2 = 0
(3 tan θ – 1)(tan θ + 2) = 0
tan θ = 1 or tan θ = –2
3
sin (90º – θ)
= cos θ
=–
p
When tan θ = 1 ,
3
Basic ∠ = 18.43º
θ = 18.43º, 198.43º
1 + p2
2.
3
– 10 tan x = 0
cos2 x
3 sec2 x – 10 tan x = 0
2
3(tan x + 1) – 10 tan x = 0
3 tan2 x + 3 – 10 tan x = 0
3 tan2 x – 10 tan x + 3 = 0
(3 tan x – 1)(tan x – 3) = 0
tan x = 1 or tan x = 3
3
When tan θ = –2,
Basic ∠ = 63.43º
θ = 116.57º, 296.57º
∴ θ = 18.43º, 116.57º, 198.43º, 296.57º
When tan x = 1 ,
3
x = 18.43º, 198.43º
When tan x = 3,
x = 71.57º, 251.57º
∴ x = 18.43º, 71.57º, 198.43º, 251.57º
30

31. WebsiteZI F505_4th pp
10/15/08
9:40 AM
Page 31
Paper 2
2. (a), (b)
1. (a) LHS =
=
=
y
1 – cos 2x
sin 2x
y = 3 sin x
2
3
2
1 – (1 – 2 sin2 x)
2 sin x cos x
O
␲
2␲
x
–2
2 sin2 x
2 sin x cos x
y = 2 – 2x
2
sin x
cos x
= tan x
= RHS
=
x
2x
+
=2
2
π
x
2x
3 sin
=2–
2
π
3 sin
(b) (i), (ii)
The graph of y = |tan x| is as shown below.
Sketch the straight line y = 2 –
x
y
y
y=
π
0
2
2π
–2
(2π, 1)
O
π
π
3π
2
π
Number of solution
= Number of intersection point
=1
x
1 – cos 2x
x
–
=0
sin 2x
2π
1 – cos 2x
x
=
sin 2x
2π
x
|tan x| =
2π
Sketch the
straight line
y= x .
2π
Number of solutions
= Number of points of intersection
=4
31
2x
π

32. WebsiteZI F506_4th pp
10/15/08
9:40 AM
Page 32
SPM ZOOM–IN
Form 5: Chapter 6 Permutations and Combinations
Paper 1
3. Number of different committees that can be
formed
1.
Number of arrangements
2
1
2
3
3P
2
2
5
Choosing a female
secretary and a female
treasurer from 7 females
3P
2
3P
2
= 4C1 ϫ 7C2 ϫ 8C3
Hence, the number of 4-digit odd numbers greater
than 2000 but less than 3000 that can be formed
= 3 ϫ 3P2
= 18
Choosing a male
president from 4 males
= 4704
2. Each group of boys and girls is counted as one
item.
B1, B2 and B3
√
This gives 2!.
G1, G2 and G3
√
√ √
√
At the same time, B1, B2, and B3 can be arranged
among themselves in their group. This gives 3!.
√ √
√
In the same way, G1, G2, and G3 can also be
arranged among themselves in their group. This
gives another 3!.
Using the multiplication principle, the total
number of arrangements
= 2! ϫ 3! ϫ 3! = 72
32
Choosing 3
subcommittee
members from 8
(males or females).

33. SPM ZOOM–IN
Form 5: Chapter 7 Probability
Paper 1
1. P(Not a green ball) = 3
5
h+5 = 3
h+k+5
5
5h + 25 = 3h + 3k + 15
2h = 3k – 10
h = 3k – 10
2
2. P (not getting any post)
=2 ϫ3 ϫ4
3
5
7
8
=
35
–
3. There are 3 ‘E’ and 4 ‘E ’ in the bag
(a) P(EE) = 3 ϫ 2 = 1
7
6 7
–
(b) P(EE ) = 3 ϫ 4 = 2
7
6 7
33

34. SPM ZOOM–IN
Form 5: Chapter 8 Probability Distributions
Paper 1
3. (a) X – Mass of a crab, in g
X ∼ N(175, 15)
1. X – Number of penalty goals scored
X ∼ B n, 3
5
P(X = 0) = 16
625
΂
΃
΂ ΃΂ ΃
Co 3
5
n
Z = X–µ
σ
= 190 – 175
15
=1
0
2
5
n
= 16
625
(b) P(175 < X < 190)
= P 175 – 175 < Z < 190 – 175
15
15
= P (0 < Z < 1)
= 0.5 – 0.1587
= 0.3413
΂
16
΂ ΃ = 625
΂ 2 ΃ =΂ 2΃
5
5
(1)(1) 2
5
n
n
4
΃
0.1587
∴n =4
O
2. X ∼ N(55, 12 )
Area of the shaded region
P (X < 37)
= P Z < 37 – 55
12
= P (Z < –1.5)
0.0668
= 0.0668
2
΂
4.
0.1841
΃
–0.9
P(Z > – 0.9) = 0.8159
∴ k = –0.9
–1.5
34
0.8159
1

35. (ii) P(10 < X < 13)
= P 10 – 12 < Z < 13 – 12
3.1201
3.1201
= P(–0.641 < Z < 0.321)
= 1 – 0.2608 – 0.3741 0.2608
= 0.3651
Paper 2
΂
1. (a) X – Number of blue beads drawn
΂ ΃
X ∼ B΂ 10, 1 ΃
3
X ∼ B 10, 6
18
0.3741
–0.641
(i) P(X ≥ 3)
= 1 – P(X = 0) – P(X = 1) – P(X = 2)
΂ ΃ ΂2΃
3
C΂1΃ ΂2΃
3
3
= 1 – 10C0 1
3
– 10
΃
0
10
2
2. (a) X – Number of customers requiring a
supplementary card
΂ ΃ ΂2΃
3
– 10C1 1
3
0.321
1
΂
΃
X ∼ B΂ 7, 14 ΃
25
9
X ∼ B 7, 280
500
8
2
= 0.7009
(i) P(X = 3)
΂ ΃ ΂ 11 ΃
25
(ii) Mean = np = 10 ϫ 1 = 3 1
3
3
= 7C3 14
25
= 0.2304
Standard deviation = npq
΂ ΃΂ ΃
C ΂ 14 ΃ ΂ 11 ΃
25
25
΂ ΃΂ ΃
5
2
= 0.1402
P(X > 8) = 90%
΂
2
7
(b) X – Lifespan of a species of dog
X ∼ N(12, σ2)
(b) X – Time taken to settle invoices
X ∼ N(30, 52)
΃
P΂ Z > –4 ΃ = 0.9
σ
P Z > 8 – 12
σ
4
(ii) P(X = 3)
= P(X = 0) + P(X = 1) + P(X = 2)
0
11 7 +7C 14 1 11 6 +
= 7C0 14
1
25
25
25
25
= 10 ϫ 1 ϫ 2
3 3
= 1.49
(i)
3
= 0.9
(i) P(28 ≤ X ≤ 36)
΂
= P 28 – 30 ≤ Z ≤ 36 – 30
5
5
= P(–0.4 ≤ Z ≤ 1.2)
= 1– 0.3446 – 0.1151
= 0.5403
0.9
0.1
–1.282
0.3446
0.1151
– 4 = –1.282
σ
–0.4
σ = 3.1201 years
35
1.2
΃

36. (ii) P(X < 22)
΂
= P Z < 22 – 30
5
= P(Z < –1.6)
= 0.0548
΃
Hence, the expected number of invoices which are
given discounts
= 0.0548 ϫ 220
= 12
36

37. SPM ZOOM–IN
Form 5: Chapter 9 Motion Along a Straight Line
Paper 2
(c) When particle A reverses its direction,
vA = 0
12 + t – t2 = 0
t2 – t – 12 = 0
(t + 3)(t – 4) = 0
t = –3 or 4
t = –3 is not accepted
∴t=4
1. (a) For particle A, at maximum velocity,
dvA = 0
dt
1 – 2t = 0
t= 1
2
d 2vA = –2 (negative)
dt 2
vB = dsB
dt
vB = 6t2 – 14t – 15
΂ ΃
Hence, vmax = 12 + 1 – 1
2
2
= 12 1 m s–1
4
2
aB = dvB
dt
aB =12t – 14
(b) sB = 2t 3 – 7t 2 – 15t
When particle B returns to O,
sB = 0
2t 3 – 7t 2 – 15t = 0
t(2t 2 – 7t – 15) = 0
t(2t + 3)(t – 5) = 0
t = 0, – 3 or 5
2
t = 0 and t = – 3 are not accepted
2
∴t=5
When t = 4,
aB =12(4) – 14 = 34 m s–2
2 (a) a = 12 – 6t
v = a dt
v = (12 – 6t) dt
v = 12t – 3t2 + c
When t = 0, v = 15. Thus, c = 15
∴ v = 12t – 3t2 + 15
At maximum velocity,
dv = 0
dt
12 – 6t = 0
t=2
sA = vA dt
sA = (12 + t – t2) dt
2
3
sA = 12t + t – t + c
2 3
When t = 0, sA = 0. ∴ c = 0
2
3
∴ sA = 12t + t – t
2
3
When t = 2,
v = 12(2) – 3(2)2 + 15 = 27 m s–1
d2v = –6 (< 0)
dt2
Therefore, v is a maximum.
When t = 5, 2
3
sA = 12(5) + 5 – 5 = 30 5 m
6
2
3
37

38. (b) s = v dt
s = (12t – 3t2 + 15) dt
s = 6t 2 – t 3 + 15t + c
When t = 0, s = 0. Thus, c = 0.
∴ s = 6t 2 – t 3 + 15t
(c) When the particle travels to the right,
v >0
12t – 3t 2 + 15 > 0
3t 2 – 12t – 15 < 0
t 2 – 4t – 5 < 0
(t + 1)(t – 5) < 0
At maximum displacement,
ds = 0
dt
12t – 3t2 + 15 = 0
3t2 – 12t – 15 = 0
t2 – 4t – 5 = 0
(t – 5)(t + 1) = 0
t = 5 or –1
t = –1 is not accepted
∴t=5
–1
5
t
–1 < t < 5
Since the values of t cannot be negative,
therefore 0 ≤ t < 5.
When t = 5,
s = 6(5)2 – 53 + 15(5) = 100 m
d 2s = 12 – 6t
dt 2
2
When t = 5, d s = 12 – 6(5) = –18
dt 2
Therefore, s is a maximum.
38

39. SPM ZOOM–IN
Form 5: Chapter 10 Motion Along a Straight Line
(c) (i) x = 4
y
3
3x = 4y
y = 3x
4
Paper 2
1. (a) I 180x + 90y ≤ 5400
2x + y ≤ 60
x
y
0
60
30
0
The furthest point on the straight line y = 3 x
4
inside the feasible region R is (20,15).
∴ xmax = 20, ymax = 15
II 3x + 4y ≤ 120
x
y
III
0
30
40
0
0
0
30
60
(ii) Profits = 200x + 150y
Draw the straight line
200x + 150y = 3000
y ≤ 2x
x
y
200 ϫ 150 ϫ 0.1 = 3000
The optimal point is (24, 12).
(b)
Hence, the maximum profit
= 200(24) + 150(12)
= RM6600
y
60
2x + y = 60
2. (a) Mixing:
30x + 10y ≤ 15 ϫ 60
3x + y ≤ 90
y = 2x
50
Baking:
40x + 40y ≤ 26 2 ϫ 60
3
x + y ≤ 40
40
30
y=
3
x
4
Decorating:
10x + 30y ≤ 15 ϫ 60
x + 3y ≤ 90
(20, 15)
20
Max (24, 12)
10
R
3x + 4y = 120
O
10
15
20
200x + 150y = 3000
30
40
x
39
x
y
0
90
30
0
x
y
0
40
40
0
x
y
0
30
90
0

40. (b)
y
90
80
70
3x + y = 90
60
50
40
Max (15, 25)
30
20
17
R
x + 3y = 90
10
5
O
x + y = 40
5x + 10y = 50
10
2023
30
40
50
(c) (i) When y = 17, xmax = 23
(ii) Profits = 5x + 10y
Draw the straight line 5x + 10y = 50.
From the graph, the optimal point is
(15, 25).
Hence, the maximum profit
= 5(15) + 10(25)
= RM325
40
60
70
80
90
x