Linear law

additionalmathematicsadditionalmat
hematicsadditionalmathematicsaddit
ionalmathematicsadditionalmathema
ticsadditionalmathematicsadditional
LINEAR LAW
mathematicsadditionalmathematicsa
Name
dditionalmathematicsadditionalmath
........................................................................................

ematicsadditionalmathematicsadditi
onalmathematicsadditionalmathemat
icsadditionalmathematicsadditional

LINEAR LAW

2.1 Understand and use the concept of lines of best fit
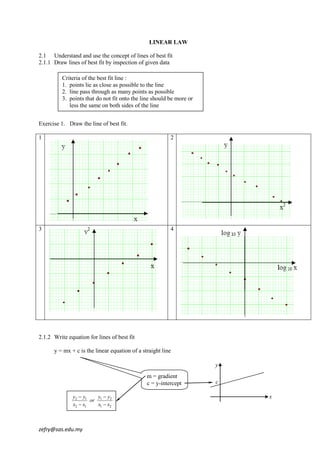
2.1.1 Draw lines of best fit by inspection of given data

Criteria of the best fit line :
1. points lie as close as possible to the line
2. line pass through as many points as possible
3. points that do not fit onto the line should be more or
less the same on both sides of the line

Exercise 1. Draw the line of best fit.

1 2

3 4

2.1.2 Write equation for lines of best fit

y = mx + c is the linear equation of a straight line

y
m = gradient
c = y-intercept c

y2  y1 y  y2 x
or 1
x2  x1 x1  x2

zefry@sas.edu.my

Exercise 2. Write the equation of the line of best fit for each of the following graphs

Example: y (ii) Example: V
(i) x (1, 6)
x
2 (4, 6)
(5, 1)
x
O
x O t
62 6 1
m m
Find m: 40 Find m: 1 5
1 
5
4
Find c: c = y-intercept Find c: V = mt + c
c=2 The line passes through (1, 6)
t , V
5
6 1  c
4
29
c
4
Substitute into y = mx + c Substitute into V= mt + c
The equation of the line : y = x + 2 5 29
The equation of the line : y   x 
4 4

a y b V
9 (1, 5)
x
(7, 1)
x (8, 1) x
O
x O t

2 17
y x
y=x+9 3 3
c F d S
x (8, 8) x
(3, 6)
x
(6, 4)
O
v O t
1

y = 2x  8
y = 3x  3

zefry@sas.edu.my

e f

y =  3x2 + 11
y = 2x2 + 6
g h

1
9 27 P v4
s t 2
2 2
i j

5 7
p q 3
6 6 p  v5
2
zefry@sas.edu.my

3.1.3 Determine the values of variables
a) from lines of best fit

Exercise 3
1 2

(2.8, 3.3) (3.6, 22)

b) from equations of lines of best fit

1 2

zefry@sas.edu.my

2.2 Applications of Linear Law to Non-linear Relations
2.2.1 Reduce non-linear relations to the linear form

LINEAR FORM OF EQUATION

Y = mX + c or Y = mX , c = 0
Variables for the y-axis Constant (no variable)
coefficient = 1 m = gradient y-intercept
Variable for the x-axis

Example : Identify Y, X, m and c for the following linear form

(i) y = 2x2  3

Y = y, m = 2, X = x2 , c = 3

y
(ii) = 3x2  5
x
y
Y= , m = 3, X = x2 , c = 5
x

Exercise 4. Reduce the following non-linear equation to linear equation in the form of Y = mX + c.
Hence, identify Y, X, m and c.

Example: Example:
3y = 5x2 + 7x y = px2
Create the y-intercept Create the y-intercept

x :
3 y 5x2 7 x
   
takelog : log10 y  log px 2
x x x
log10 y  log10 p  log10 x 2
3y
 5x  7 log10 y  log10 p  2 log10 x
x
Create coefficient of y = 1 & Create coefficient of y = 1 &
arrange in the form Y = mX + c arrange in the form Y = mX + c
3 y 5x 7 log10 y  2 log10 x  log10 p
3 :  
3x 3 3
y 5x 7
 
x 3 3
Compare to Y = mX + c Compare to Y = mX + c
y 5x 7 log10 y  2 log10 x  log10 p
 
x 3 3
y 5 7 Y =log10 y, m = 2, X = log10 x, c = log10 p
Y = , m = , X = x, c =
x 3 3

zefry@sas.edu.my

Equation Y = mX + c Y X m c
a) y2 = ax + b

b) y = ax2 + bx

c) y2 = 5x2 + 4x

d) 5
y= c
x
e) xy = a + bx
a
f) xy   bx
x

g) y = a ( x+ b)2

h) y= a x b
x

a b
i)  1
y x

j) y = abx

zefry@sas.edu.my

2.2.2a Determine values of constants of non-linear relations when given lines of best fit
Example :
a
The variables x and y are related by the equation by  x  where a and b are constants.
x
The diagram below shows part of a line of best fit obtained by plotting a graph of xy against x2.
Find the values of a and b. xy

(4, 50)
(1, 35)

O
x2
From the graph identify the representation of y-axis and x-axis
Y = xy, X = x2
Reduce the equation given to linear form, Y = mX + c
by x a
b :  
 b  b  b  x
x a
y 
b bx
x  x a  x
x :  x  y  
b bx
1 a
xy  x 2 
b b
Compare with Y = mX + c
1 a
Y = xy , m = , X = x2 , c =
b b
50  35
Find m from the graph : m 5
4 1
Find c, substitute X = 1, Y = 35, m = 5 into the equation Y = mX + c
35 = 5 (1) + c
c = 30
a
1  30
m 5 b
b a
Find the variables a and b :  30
1 1
b
5 5
a6

Exercise 5.
1 2

[y = 2x + 4] [y2 = 5(1/x) + 2]
zefry@sas.edu.my

3 4

5 6

zefry@sas.edu.my

7 y 8 y2
x
(2, 9) 
(4, 10)

(2, 6)
(6, 1)
x 1
x
The variables x and y are related by the equation The variables x and y are related by the equation
y = px2 + qx. k
y 2   c . Find
Find the values of p and q. x
(i) the value of k and c
(ii) the value of x when y = 2

p = 2, q = 13 (i) k = 2, c = 2 (ii) x = 1
9 y 10 log y

 (3, 6) 1(1, 9)

1
1 1 log x
x
The above figure shows part of a straight line The above figure shows part of a straight line
graph drawn to represent the equation of graph drawn to represent the equation of
xy = a + bx. y = axb.
Find the value of a and b. Find the value of a and b.

a = 3, b = 3 a = 11, b = 8

zefry@sas.edu.my

2.2.2b Determine values of constants of non-linear relations when given data

A. Using a graph paper
1. Identify the graph to be drawn
2. Change the non-linear function with variables x and y
to a linear form Y = mX + c
3. Construct a table for X and Y
4. Choose a suitable scale & label both axes
5. Draw line of best fit
6. Determine : gradient , m and Y-intercept , c from the graph to find the values of
constants in the non-linear equation.

Example:
The table shows the corresponding values of two variables, x and y, obtained from an experiment.
k
The variables x and y are related by the equation y  hx  , where h and k are constants
hx

x 1.0 2.0 3.0 4.0 5.0 6.0
y 6.0 4.7 5.2 6.2 7.1 7.9

a) Using a scale of 2 cm to 10 units on both axes, plot a graph of xy against x2.
Hence, draw a line of best fit.
b) Use your graph from (a) to find the value of
(i) h,
(ii) k.

Solution :
1. Drawn graph : Y = xy and X = x2.
2. Change non-linear to linear form.
k
y  hx 
hx
k  x
 x:  x  y  hx  x  
hx
k
xy  hx  2
h
k
Y  xy, X  x , m  h, c 
2
h
3.
x 1.0 2.0 3.0 4.0 5.0 6.0
y 6.0 4.7 5.2 6.2 7.1 7.9
x2 1.0 4.0 9.0 16.0 25.0 36.0
xy 6.0 9.4 15.6 24.8 35.5 47.4

37
6. From the graph, gradient , m   1.233
30
Hence, h = 1.233

From the graph, Y-intercept , c = 4.5
h
 4.5
k
k
Hence,  4. 5
1.233
k  5.549

zefry@sas.edu.my

xy

50
0
x

45

40
0

x
35

30
0

25 x

20
0

x
15
0

10
x
0

x
5

0 5 10 15 20 25 30 35 40 x2
0 0 0 0 0 0

zefry@sas.edu.my

Exercise 6.
1. The table below shows some experimental data of two related variable x and y. It is known that
x and y are related by an equation in the form y = ax + bx2, where a and b are constants.

x 1 2 3 4 5 6 7
y 7 16 24 24 16 0 24

y
a) Draw the straight line graph of against x.
x
b) Hence, use the graph to find the values of a and b.
a = 1, b = 10

2. The table below shows some experimental data of two related variable x and y.

x 0 2 4 6 8 10
y 1.67 1.9 2.21 2.41 2.65 2.79

It is known that x and y are related by an equation in the form
ax b
y  , where a and b are constants.
y y
a) Draw the straight line graph of y2 against x.
b) Hence, use the graph to find the values of a and b.
a = 0.5, b = 2.8
3. The table below shows two variable x and y, which are obtained from an experiment. The
r
variables are related by the equation y  px  , where p and r are constants.
px

x 0 2 4 6 8 10
y 1.67 1.9 2.21 2.41 2.65 2.79

a) Plot xy against x2. Hence draw the line of best fit.

b) Based on the graph, find the values of p and r.
p =1.38, r = 5.52

zefry@sas.edu.my

Linear law

More Related Content

What's hot

Viewers also liked

Similar to Linear law

Linear law