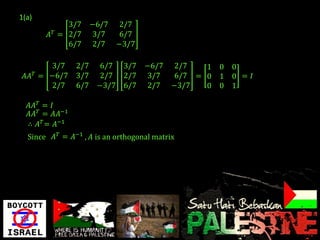
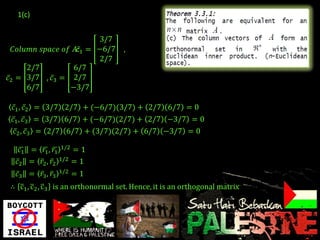
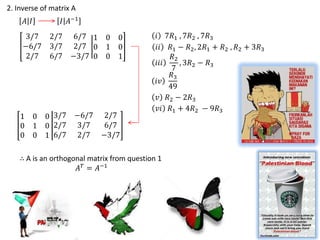
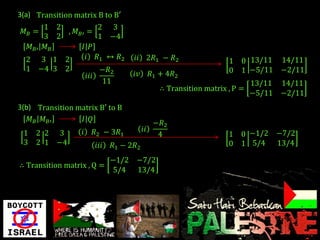
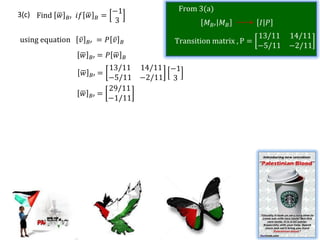
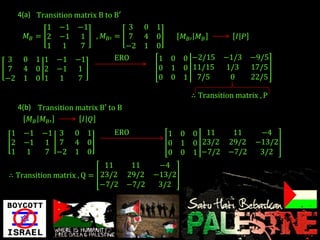
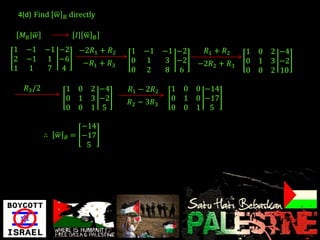
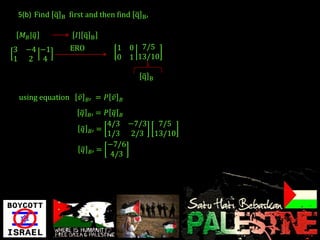
The document provides information about linear algebra tutorial 7. It discusses properties of orthogonal matrices including: - Matrix A is an orthogonal matrix since AT = A-1 - The rows and columns of A form orthonormal sets, confirming A is orthogonal - Methods to find the inverse and transition matrices between different bases are presented. Properties of orthogonality and procedures for working with orthogonal matrices are examined through examples.

2. TUTORIAL 7
MTH3201 LINEAR ALGEBRA

3. 1(a)
3/7 −6/7 2/7
𝐴 𝑇 = 2/7 3/7 6/7
6/7 2/7 −3/7
3/7 2/7 6/7 3/7 −6/7 2/7 1 0 0
𝑇
𝐴𝐴 = −6/7 3/7 2/7 2/7 3/7 6/7 = 0 1 0 = 𝐼
2/7 6/7 −3/7 6/7 2/7 −3/7 0 0 1
𝐴𝐴 𝑇 = 𝐼
𝐴𝐴 𝑇 = 𝐴𝐴−1
∴ 𝐴 𝑇 = 𝐴−1
Since 𝐴 𝑇 = 𝐴−1 , 𝐴 is an orthogonal matrix

4. 1(b)
𝑅𝑜𝑤 𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 𝐴: 𝑟1 = 3/7 2/7 6/7
𝑟2 = −6/7 3/7 2/7
𝑟3 = 2/7 6/7 −3/7
𝑟1 , 𝑟2 = 3/7 −6/7 + (2/7)(3/7) + 6/7 2/7 = 0
𝑟1 , 𝑟3 = 3/7 2/7 + (2/7)(6/7) + 6/7 −3/7 = 0
𝑟2 , 𝑟3 = −6/7 2/7 + (3/7)(6/7) + 2/7 −3/7 = 0
𝑟1 = 𝑟1 , 𝑟1 1/2 = 3/7 2 + 2/7 2 + 6/7 2 = 1
𝑟2 = 𝑟2 , 𝑟2 1/2 = −6/7 2 + 3/7 2 + 2/7 2 = 1
𝑟3 = 𝑟3 , 𝑟3 1/2 = 2/7 2 + 6/7 2 + −3/7 2 =1
∴ r1 , r2 , r3 is an orthonormal set. Hence, it is an orthogonal matrix

5. 1(c)
3/7
𝐶𝑜𝑙𝑢𝑚𝑛 𝑠𝑝𝑎𝑐𝑒 𝑜𝑓 𝐴:𝑐1 = −6/7 ,
2/7
2/7 6/7
𝑐2 = 3/7 , 𝑐3 = 2/7
6/7 −3/7
𝑐1 , 𝑐2 = 3/7 2/7 + (−6/7)(3/7) + 2/7 6/7 = 0
𝑐1 , 𝑐3 = 3/7 6/7 + (−6/7)(2/7) + 2/7 −3/7 = 0
𝑐2 , 𝑐3 = 2/7 6/7 + (3/7)(2/7) + 6/7 −3/7 = 0
𝑐1 = 𝑟1 , 𝑟1 1/2 = 1
𝑐2 = 𝑟2 , 𝑟2 1/2 = 1
𝑐3 = 𝑟3 , 𝑟3 1/2 =1
∴ c1 , c2 , c3 is an orthonormal set. Hence, it is an orthogonal matrix

6. 2. Inverse of matrix A
𝐴 𝐼 𝐼 𝐴−1
3/7 2/7 6/7 1 0 0 𝑖 7𝑅1 , 7𝑅2 , 7𝑅3
−6/7 3/7 2/7 0 1 0 𝑖𝑖 𝑅1 − 𝑅2 , 2𝑅1 + 𝑅2 , 𝑅2 + 3𝑅3
2/7 6/7 −3/7 0 0 1 𝑅2
𝑖𝑖𝑖 , 3𝑅2 − 𝑅3
7
𝑅3
𝑖𝑣
49
𝑣 𝑅2 − 2𝑅3
𝑣𝑖 𝑅1 + 4𝑅2 − 9𝑅3
1 0 0 3/7 −6/7 2/7
0 1 0 2/7 3/7 6/7
0 0 1 6/7 2/7 −3/7
∴ A is an orthogonal matrix from question 1
𝐴 𝑇 = 𝐴−1

7. 3(a) Transition matrix B to B′
1 2 2 3
𝑀𝐵 = , 𝑀 𝐵′ =
3 2 1 −4
𝑀 𝐵′ 𝑀 𝐵 𝐼 𝑃
2 3 1 2 𝑖 𝑅1 ↔ 𝑅2 𝑖𝑖 2𝑅1 − 𝑅2 1 0 13/11 14/11
1 −4 3 2 −𝑅2 0 1 −5/11 −2/11
𝑖𝑖𝑖 𝑖𝑣 𝑅1 + 4𝑅2
11 13/11 14/11
∴ Transition matrix , P =
−5/11 −2/11
3(b) Transition matrix B′ to B
𝑀 𝐵 𝑀 𝐵′ 𝐼 𝑄 −𝑅2
𝑖 𝑅2 − 3𝑅1 𝑖𝑖
1 2 2 3 4 1 0 −1/2 −7/2
3 2 1 −4 𝑖𝑖𝑖 𝑅1 − 2𝑅2 0 1 5/4 13/4
−1/2 −7/2
∴ Transition matrix , Q =
5/4 13/4

8. −1 From 3(a)
3(c) Find 𝑤 𝐵′ 𝑖𝑓 𝑤 𝐵 =
3 𝑀 𝐵′ 𝑀 𝐵 𝐼 𝑃
using equation 𝑣 = 𝑃 𝑣 13/11 14/11
𝐵′ 𝐵 Transition matrix , P =
−5/11 −2/11
𝑤 𝐵′ = 𝑃 𝑤 𝐵
13/11 14/11 −1
𝑤 𝐵′ =
−5/11 −2/11 3
29/11
𝑤 𝐵′ =
−1/11

9. 4(a) Transition matrix B to B′
1 −1 −1 3 0 1
𝑀𝐵 = 2 −1 1 , 𝑀 𝐵′ = 7 4 0 𝑀 𝐵′ 𝑀 𝐵 𝐼 𝑃
1 1 7 −2 1 0
3 0 1 1 −1 −1 ERO 1 0 0 −2/15 −1/3 −9/5
7 4 0 2 −1 1 0 1 0 11/15 1/3 17/5
−2 1 0 1 1 7 0 0 1 7/5 0 22/5
∴ Transition matrix , P
4(b) Transition matrix B′ to B
𝑀 𝐵 𝑀 𝐵′ 𝐼 𝑄
1 −1 −1 3 0 1 ERO 1 0 0 11 11 −4
2 −1 1 7 4 0 0 1 0 23/2 29/2 −13/2
1 1 7 −2 1 0 0 0 1 −7/2 −7/2 3/2
11 11 −4
∴ Transition matrix , Q = 23/2 29/2 −13/2
−7/2 −7/2 3/2

10. From 4(a)
4(c) Find w B′ first and then find w B
𝑀 𝐵′ 𝑀 𝐵 𝐼 𝑃
𝑀 𝐵′ 𝑤 𝐼 w B′ 13/11 14/11
Transition matrix , P =
3 0 1 −2 1 0 0 −22/15 −5/11 −2/11
ERO
7 4 0 −6 0 1 0 16/15
−2 1 0 4 0 0 1 12/5
w B′
using equation 𝑣 𝐵 = 𝑃−1 𝑣 𝐵′
𝑤 𝐵 = 𝑃−1 𝑤 𝐵′
𝑤= 𝑄 𝑤 𝐵′
𝐵
11 11 −4 −22/15
𝑤 𝐵 = 23/2 29/2 −13/2 16/15
−7/2 −7/2 3/2 12/5
−14
𝑤 𝐵 = −17
5

11. 4(d) Find w B directly
𝑀𝐵 𝑤 𝐼 w B
1 −1 −1 −2 −2𝑅1 + 𝑅2 1 −1 −1 −2 𝑅1 + 𝑅2 1 0 2 −4
2 −1 1 −6 0 1 3 −2 0 1 3 −2
−𝑅1 + 𝑅3 −2𝑅2 + 𝑅3
1 1 7 4 0 2 8 6 0 0 2 10
𝑅3 /2 1 0 2 −4 𝑅1 − 2𝑅2 1 0 0 −14
0 1 3 −2 𝑅2 − 3𝑅3 0 1 0 −17
0 0 1 5 0 0 1 5
−14
∴ 𝑤 𝐵 = −17
5

12. 5(a) Transition matrix B to B′
3 −4 2 1
𝑀𝐵 = , 𝑀 𝐵′ =
1 2 0 3
𝑀 𝐵′ 𝑀 𝐵 𝐼 𝑃
2 1 3 −4
0 3 1 2
𝑖 𝑅1 /2
𝑖𝑖 𝑅2 /3
𝑅2
𝑖𝑖𝑖 𝑅1 −
2
1 0 4/3 −7/3
0 1 1/3 2/3
4/3 −7/3
∴ Transition matrix , P =
1/3 2/3

13. 5(b) Find q B first and then find q B′
𝑀𝐵 𝑞 𝐼 q B
3 −4 −1 ERO 1 0 7/5
1 2 4 0 1 13/10
q B
using equation 𝑣 𝐵′ = 𝑃 𝑣 𝐵
𝑞 = 𝑃 𝑞 𝐵
𝐵′
4/3 −7/3 7/5
𝑞 𝐵′ =
1/3 2/3 13/10
−7/6
𝑞 𝐵′ =
4/3

14. 5(c) Find q B′ directly
𝑀 𝐵′ 𝑞 𝐼 q B′
2 1 −1 𝑅1 /2
1 1/2 −1/2
0 3 4 𝑅2 /3 0 1 4/3
−𝑅2
+ 𝑅1
2 1 0 −7/6
0 1 4/3
−7/6
∴ 𝑞 𝐵′ =
4/3