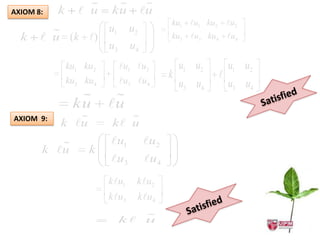
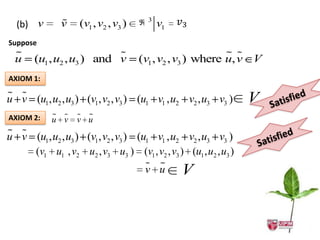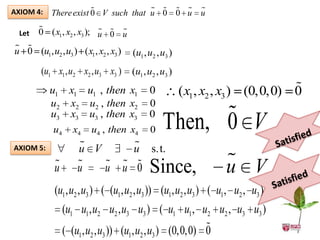The document provides examples to determine if given sets with operations are vector spaces by checking if they satisfy the 10 axioms of a vector space. Set 1 of 2x2 non-singular matrices is not a vector space as it fails axioms 4 and 5. Set 2 of triples of real numbers is a vector space as it satisfies all axioms. Set 3 is not a vector space as it fails axiom 4.

1. Tutorial MTH 3201
Linear Algebras

2. Tutorial 1

3. 1. Determine whether the given set V with the given operations is a vector
space or not. For those that are NOT, list all axioms that fail to hold.
(a) V is the set of all 2 × 2 non-singular matrices. The operations of
addition and scalar multiplication are the standard matrix
operations. V=2 × 2 non-singular matrices Operation=-standard matrix operations.
Let
Suppose u1 u2 v1 v2

u 
and v
u3 u4 v3 v4
AXIOM 1:
u1 u2 v1 v2 u1 v1 u2 v2
 
u v V
u3 u4 v3 v4 u3 v3 u4 v4
AXIOM 2:    
u v v u
u1 u2 v1 v2 u1 v1 u2 v2 v1 u1 v2 u2 u1 u2 v1 v2
 
u v
u3 u4 v3 v4 u3 v3 u4 v4 v3 u3 v4 u4 u3 u4 v3 v4
 
v u V

4. AXIOM 3:
   u1 u2 v1 v2 w1 w2
u (v w)
u3 u4 v3 v4 w3 w4
u1 u2 v1 w1 v2 w2
u3 u4 v3 w3 v4 w4
u1 v1 w1 u2 v2 w2
u3 v3 w3 u4 v4 w4 V
   u1 u2 v1 v2 w1 w2
(u v) w
u3 u4 v3 v4 w3 w4
u1 v1 u2 v2 w1 w2
u3 v3 u4 v4 w3 w4
u1 v1 w1 u2 v2 w2
V
u3 v3 w3 u4 v4 w4
     
u (v w) (v u ) w

5. AXIOM 4:     
There exist 0 V such that u 0 0 u 
u
Let x1 x2

0 ; u 0 u
  
x3 x4
u1 u2 x1 x2 u1 u2
 
u 0
u3 u4 x3 x4 u3 u4
u1 x1 u2 x2 u1 u2
u3 x3 u4 x4 u3 u4
u1 x1 u1 , then x1 0  V
Then, 0
u2 x2 u2 , then x2 0
u3 x3 u3 , then x3 0
u4 x4 u4 , then x4 0

But 0 0 which is a singular matrix

6. AXIOM 5: 
u V 
u 
s.t. u 
u 
u  
u 0
 V
Since, 0
AXIOM 6:
 
If k is any scalar and u V then ku V .
 k u1 u2 ku1 ku2
ku
u3 u4
V
ku3 ku4
AXIOM 7: 
k u 
v 
ku 
kv
  u1 u2 v1 v2
k u v k
u3 u4 v3 v4
u1 u2 v1 v2  
k k ku kv V
u3 u4 v3 v4

7. AXIOM 8: k 
 u 
ku 
u
ku1 u1 ku2 u2
 u1 u2
k  u ( k ) ku3 u3 ku4 u4
u3 u4
ku1 ku2 u1 u2 u1 u2 u1 u2
ku3 ku4 u3 u4
k 
u3 u4 u3 u4

ku 
u
AXIOM 9: 
k u 
k u
 u1 u 2
k u k
u3 u 4
k u1 k u2
k u3 k u4

k u

8. AXIOM 10:  
11 u 
u
u1 u2 u1 u2
1
u 1 
u
u3 u4 u3 u4
CONCLUSION :
Hence, V is is not a vector space
since Axiom 4 and Axiom 5 aren't satisfied.

9. V=2 × 2 non-singular matrices
• i.e., one that has a matrix inverse (invertable)
• A square matrix is nonsingular iff its
determinant is nonzero.
Example:
0 0
0 0
 V
0

10. (b) v 
v (v1 , v2 , v3 )  3 v1 v2
Suppose

u 
(u1 , u2 , u3 ) and v  
(v1 , v2 , v3 ) where u, v V
AXIOM 1:
 
u v (u1, u2 , u3 ) (v1, v2 , v3 ) (u1 v1 , u2 v2 , u3 v3 ) V
AXIOM 2:    
u v v u
 
u v (u1, u2 , u3 ) (v1, v2 , v3 ) (u1 v1 , u2 v2 , u3 v3 )
(v1 u1 , v2 u2 , v3 u3 ) (v1 , v2 , v3 ) (u1 , u2 , u3 )
 
v u V

11. AXIOM 3:      
u (v w) (v u ) w
  
u (v w) (u1, u2 , u3 ) (v1, v2 , v3 ) (w1, w2 , w3 )
(u1, u2 , u3 ) v1 w1 , v2 w2 , v3 w3
(u1 v1 w1 , u2 v2 w2 , u3 v3 w3 ) V
  
(u v) w (u1, u2 , u3 ) (v1, v2 , v3 ) (w1, w2 , w3 )
u1 v1, u2 v2 , u3 v3 (w1, w2 , w3 )
(u1 v1 w1 , u2 v2 w2 , u3 v3 w3 ) V
     
u (v w) (v u ) w

12. AXIOM 4:     
There exist 0 V such that u 0 0 u 
u
Let    
0 ( x1, x2 , x3 ); u 0 u
 
u 0 (u1, u2 , u3 ) ( x1, x2 , x3 ) (u1 , u2 , u3 )
(u1 x1 , u2 x2 , u3 x3 ) (u1 , u2 , u3 )
u1 x1 u1 , then x1 0 
( x1, x2 , x3 ) (0,0,0) 0
u2 x2 u2 , then x2 0
u3 x3 u3 , then x3
u4 x4 u4 , then x4
0
0
 V
Then, 0
AXIOM 5: 
u V 
u s.t.

u 
u   
u u 0 Since,  V
u
(u1 , u2 , u3 ) ( (u1 , u2 , u3 )) (u1, u2 , u3 ) ( u1, u2 , u3 )
(u1 u1 , u2 u2 , u3 u3 ) ( u1 u1 , u2 u2 , u3 u3 )

( (u , u , u )) (u , u , u ) (0,0,0) 0
1 2 3 1 2 3

13. AXIOM 6:
If k is any scalar and  
u V then ku V.
 (ku1 , ku2 , ku3 )
ku k u1 , u2 , u3 V
AXIOM 7:

k u 
v 
ku 
kv
 
k u v k (u1 , u2 , u3 ) (v1 , v2 , v3 )
k (u1 , u2 , u3 ) k (v1 , v2 , v3 )
 
ku kv V

14. AXIOM 8: k 
 u 
ku 
u
k 
 u (k ) u1, u2 , u3 (ku1 u1 , ku2 u2 , ku3 u3 )
(ku1 , ku2 , ku3 ) (u1 , u2 , u3 )
k u1, u2 , u3  u1, u2 , u3

ku 
u
AXIOM 9: 
k u 
k u

k u k u1 , u2 , u3
(k u1 , k u2 , k u3 )

k u

15. AXIOM 10: 1 
1 u 
u
1 1(u1 , u2 , u3 )
u (u1 , u2 , u3 ) 
u
CONCLUSION :
Hence, V is a vector space.

16. (c) v 
v (v1 , v2 , v3 )  3 v1 v2
Suppose

u 
(u1 , u2 , u3 ) and v  
(v1 , v2 , v3 ) where u, v V
AXIOM 1:
 
u v (u1, u2 , u3 ) (v1, v2 , v3 ) (u1 v1 , u2 v2 , u3 v3 ) V
AXIOM 2:    
u v v u
 
u v (u1, u2 , u3 ) (v1, v2 , v3 ) (u1 v1 , u2 v2 , u3 v3 )
(v1 u1 , v2 u2 , v3 u3 ) (v1 , v2 , v3 ) (u1 , u2 , u3 )
 
v u V

17. AXIOM 3:      
u (v w) (v u ) w
  
u (v w) (u1, u2 , u3 ) (v1, v2 , v3 ) (w1, w2 , w3 )
(u1, u2 , u3 ) v1 w1 , v2 w2 , v3 w3
(u1 v1 w1 , u2 v2 w2 , u3 v3 w3 ) V
  
(u v) w (u1, u2 , u3 ) (v1, v2 , v3 ) (w1, w2 , w3 )
u1 v1, u2 v2 , u3 v3 (w1, w2 , w3 )
(u1 v1 w1 , u2 v2 w2 , u3 v3 w3 ) V
     
u (v w) (v u ) w

18. AXIOM 4:     
There exist 0 V such that u 0 0 u 
u
Let    
0 ( x1, x2 , x3 ); u 0 u
 
u 0 (u1, u2 , u3 ) ( x1, x2 , x3 ) (u1 , u2 , u3 )
(u1 x1 , u2 x2 , u3 x3 ) (u1 , u2 , u3 )

( x1, x2 , x3 ) (0,0,0) 0
Hence v1 v2 .Then, 
0 V.
AXIOM 5:
 V
Since, 0

19. AXIOM 6:
If k is any scalar and  
u V then ku V.
 (ku1 , ku2 , ku3 )
ku k u1 , u2 , u3 V
AXIOM 7:

k u 
v 
ku 
kv
 
k u v k (u1 , u2 , u3 ) (v1 , v2 , v3 )
k (u1 , u2 , u3 ) k (v1 , v2 , v3 )
 
ku kv V

20. AXIOM 8: k 
 u 
ku 
u
k 
 u (k ) u1, u2 , u3 (ku1 u1 , ku2 u2 , ku3 u3 )
(ku1 , ku2 , ku3 ) (u1 , u2 , u3 )
k u1, u2 , u3  u1, u2 , u3

ku 
u
AXIOM 9: 
k u 
k u

k u k u1 , u2 , u3
(k u1 , k u2 , k u3 )

k u

21. AXIOM 10: 1
u 
u
1 1(u1 , u2 , u3 )
u (u1 , u2 , u3 ) 
u
CONCLUSION :
Hence, V is not a vector space because
Axiom 4 and Axiom 5 not satisfied.

22. 2. x1
v 
x x1 , x2 
x2
u1 v1 u1 v1 u1 ku1 1
 
u v 
ku k
u2 v2 u2 v2 u2 ku2 1

a) u ( 1, 2) 
v (3, 4)
1 3 2   1 3
 
i) u v iii ) 5u 5v 5 5
2 4 2 2 4
1 2 5( 1) 1 5(3) 1
( 1) 1
1 1 1 3 3 5(2) 1 5( 4) 1
ii ) u
3 3 2 1 1 4 16 12
(2) 1
3 3 9 21 12

23.  v) 5 2
iv)5( u 
5(2) 1 11
2 5( 2) 1 11
 1 5( 1) 1 4

v) (2 5) u 5u 5
2 5(2) 1 9
  1 1
vi ) 2u 3u 2 3
2 2
2( 1) 1 5( 1) 1
2(2) 1 3(2) 1
3 2 1
5 5 0

24. 
(b) Find the object 0 
V such that 0 
u  
u for any u V.
 x1 u1
Suppose 0 
and u
x2 u2
  x1 u1 u1
0 u
x2 u2 u2
x1 u1 u1
x2 u2 u2
Then x1 u1 u1 x1 0
x2 u2 u2 x2 0.
 0
0 V
0

25. 
(c) If the object 0 in (b) exist,
    
find the object w V such that u w 0 for any u V .
 0 w1 u1
Suppose 0 
,w 
and u
0 w2 u2
w1 u1 0
 
w u
w2 u2 0
w1 u1 0
w2 u2 0
Then w1 u1 0 w1 u1
w2 u2 0 w2 u2 .
u1

w V
u2

26. 
(d) Is 1v  
v for each v V?
v1

Suppose v
v2
v1

1v 1
v2
1(v1 ) 1 v1
1(v2 ) 1 v2

27. 
(e) Is v with the given two operation a vector space?
V is not a vector space because
Axiom 8 is not satisfied.

28. 3. x1
v 
x x1 , x2 
x2
u1 v1 u1v1 u1 u1 k
 
u v 
ku k
u2 v2 u2 v2 u2 ku2

a) u ( 2, 7) 
v (1, 2)
  2 1
2 1 2(1) 2 iii ) 3u 3v 3 3
 
i) u v 7 2
7 2 7 2 5
3( 2)(1) 3 1
1 3
2 3(7) 3( 2)
1 1 2 2 2
ii ) u
2 2 7 1 7 1 4 4
(7)
2 2 21 6 15

29.  v) 3( 2 )
iv)3( u 
3 2 21
5 3(5) 15
 2 2 7 5

v) (2 5) u 7u 7
7 7(7) 49
  2 2
vi ) 2u 5u 2 5
7 7
2 2 5 2
2(7) 5(7)
0 3 0
14 35 49

30. 
(b) Find the object 0 
V such that 0 
u  
u for any u V.
 x1 u1
Suppose 0 
and u
x2 u2
  x1 u1 u1
0 u
x2 u2 u2
x1u1 u1
x2 u2 u2
Then x1u1 u1 x1 1
x2 u2 u2 x2 0.
 1
0 V
0

31. 
(c) If the object 0 in (b) exist,
    
find the object w V such that u w 0 for any u V .
 1 w1 u1
Suppose 0 
,w 
and u
0 w2 u2
w1 u1 1 1
Then w1u1 1 w1
 
w u u1
w2 u2 0
w2 u2 0 w2 u2 .
w1u1 1 1
w2 u2 0 
w u1 V
u2

32. (d) Is (k 
)v 
kv  
v for each v V and k ,  ?
v1

Suppose v
v2
v1 (k ) v1

( k  )v ( k )
v2 (k )v2
v1 v1 k v1  v1 (k v1 )( v1 )
 
kv v k 
v2 v2 kv2 v2 kv2 v2

(k )v  
kv v

33. 
(e) Is v with the given two operation a vector space?
V is not a vector space because
Axiom 8 is not satisfied.

34. v 
x u1 , u2 (v1 v2 ) u1 , u2 , v1 , v2 
4.
 
u v (u1 , u2 ) (v1 , v2 ) (u1 v1 , 0)

ku k (u1 , u2 ) ( ku1 , ku2 )

a) u ( 3, 2) 
v ( 1,5)
 
i) u v ( 3, 2) ( 1,5)  
iii ) 2u 2v 2 3, 2 2( 1,5)
( 3 ( 1),0) ( 4,0) ( 6, 4) ( 2,10)
1 1 ( 8, 0).
ii ) u ( 3, 2)
2 2
1 1 3
( ( 3), (2)) ( ,1)
2 2 2

35.  
iv) 2( u v) 2( 4,0) 8,0
 
v) (2 5) u 7u 7( 3, 2)
(7( 3),7(2)) ( 21,14)
 
vi ) 2u 5u 2( 3, 2) 5( 3, 2)
( 6, 4) ( 15,10)
( 21,0)

36. 
(b) Find the object 0 
V such that 0 
u  
u for any u V.

Suppose 0 ( x1 , x2 ) 
and u (u1 , u2 )
 
0 u ( x1, x2 ) (u1, u2 ) (u1, u2 )
( x1 u1 , 0) (u1 , u2 )
Then x1 u1 u1 x1 0
0 u2 x2 0.
 0
0 V
0

37. 
(c) If the object 0 in (b) exist,
    
find the object w V such that u w 0 for any u V .
 
Since 0 not exist and then w is not exist.

38. (d) Is 
k (v 
w) 
kv   
kw for each v, w V and k ?

Suppose v v1, v2 
and w (w1, w2 )
 
k (v w ) k (v1 , v2 ) k ( w1 , w2 ) (kv1 , kv2 ) (kw1 , kw2 )
(kv1 kw1 , 0)
 
kv kw k (v1 , v2 ) k ( w1 , w2 ) (kv1 , kv2 ) (kw1 , kw2 )
(kv1 kw1 , 0)

k (v 
w) 
kv 
kw

39. 
(e) Is v with the given two operation a vector space?
V is not a vector space since

0 is not exist.

40. 5. Is the set W subspace of vector space V
From lecture note,

41. 5. Is the set W subspace of vector space V
a) W u1 , u2 , u3  3 u1 u2 u3 
 
Let u (u2 u3 , u2 , u3 ) v (v2 v3 , v2 , v3 )
Axiom1
 
( u v) (u2 u3 , u2 , u3 ) (v2 v3 , v2 , v3 )
((u2 v2 ) (u3 v3 ), u2 v2 , u3 v3 ) W
Axiom 6

k u k (u u3 , u2 , u3 ) W
2
W is subspace of V

42. 5. Is the set W subspace of vector space V
b) W x, y 2 x 0 ; V 
 
Let u (u1 , u2 ) v (v1 , v2 )
Axiom1
 
( u v) (u1 , u2 ) (v1 , v2 )
(u1 v1 , u2 v2 ) W
Axiom 6

ku k (u1 , u2 ) (ku1 , ku2 )
If k 0, then ku1 0 W
W is not subspace of V

43. 5. Is the set W subspace of vector space V
2 2
c) W x, y  y 2x ; V 
 
Let u (u1 , 2u1 ) v (v1 , 2v1 )
Axiom1
 
( u v) (u1 , 2u1 ) (v1 , 2v1 )
(u1 v1 , 2(u1 v1 )) W
Axiom 6

k u k (u1 , 2u1 ) (ku1 , 2ku2 ) W
W is subspace of V

44. 5. Is the set W subspace of vector space V
d) W p x P2 p(0) 0 ; V P2
Let P ( x) a1 x n b1 x n
1
1
... 0
P2 ( x) a2 x n b2 x n 1
... 0
Axiom1
P ( x) P2 ( x) a1 x n b1 x n
1
1
... 0 a2 x n b2 x n 1
... 0
(a1 a2 ) x n (b1 b2 ) x n 1
... 0 W
Axiom 6
kP ( x) k (a1 x n b1 x n
1
1
... 0) ka1 x n kb1 x n 1
... 0 W
W is subspace of V

45. 5. Is the set W subspace of vector space V
e) W p ( x) ax 2 3x 2a  ; V P( x)
Let P ( x) a1 x 2 3x 2
1
P2 ( x) a2 x 2 3 x 2
Axiom1
P ( x) P2 ( x) a1 x 2 3x 2 a2 x 2 3x 2
1
(a1 a2 ) x 2 6 x 4 W
Axiom 6
kP ( x) k (a1 x 2 3x 2) ka1 x 2 3kx 6 W
1
W is not subspace of V

46. 5. Is the set W subspace of vector space V
a c
f) W a, c  ; V M 22
c a
u1 u2 v1 v2

Let u 
v
u2 u4 v2 v4
Axiom1
u1 u2 v1 v2 u1 v1 u2 v2
 
u v W
u2 u4 v2 v4 u2 v2 (u4 v4 )
Axiom 6
u1 u2 ku1 ku2

ku k
u2 u4 ku2 ku4
If k 0, then ku1 0 W
W is not subspace of V

47. 5. Is the set W subspace of vector space V
a b
g) W a, b, c  ; V M 22
c 0
u1 u2 v1 v2

Let u 
v
u2 0 v2 0
Axiom1
u1 u2 v1 v2 u1 v1 u2 v2
 
u v W
u2 0 v2 0 u2 v2 (0 0)
Axiom 6
u1 u2 ku1 ku2

ku k W
u2 0 ku2 0
W is subspace of V

48. Thank You!!!
“Satu itu Alif, Alif itu Ikhlas,
Ikhlas itu perlu diletakkan pada tempat Pertama,
Juga Perlu di Utamakan”