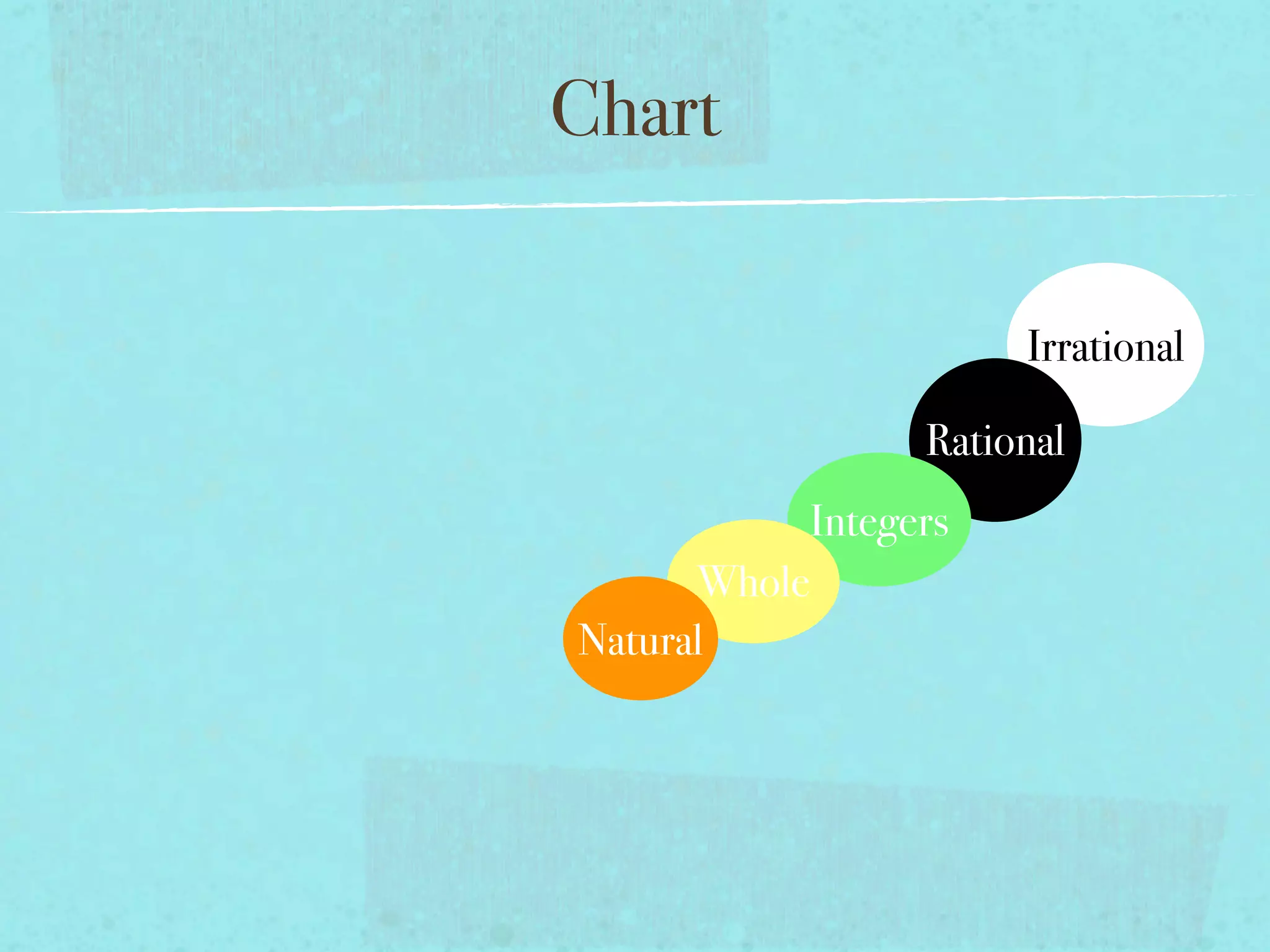
The document discusses different types of real numbers including natural numbers, whole numbers, integers, rational numbers, and irrational numbers. Natural numbers can be defined as positive integers or non-negative integers. Whole numbers are sometimes used to refer to non-negative integers, positive integers, or all integers. Rational numbers are numbers that can be expressed as fractions, while irrational numbers like √2 have decimal expansions that continue forever without repeating.

1. Real Numbers

2. Real Numbers
By Kristle Wilson

3. By Kristle Wilson

5. What are Natural Numbers

6. What are Natural Numbers
In math, there are two conventions for the set of
natural numbers: it is either the set of positive
integers {1, 2, 3, ...} according to the traditional
definition or the set of non-negative integers {0,
1, 2, ...} according to a definition first appearing
in the nineteenth century.

7. What are Natural Numbers
In math, there are two conventions for the set of
natural numbers: it is either the set of positive
integers {1, 2, 3, ...} according to the traditional
definition or the set of non-negative integers {0,
1, 2, ...} according to a definition first appearing
in the nineteenth century.
Natural numbers have two main purposes: counting
("there are 6 coins on the table") and ordering ("this
is the 3rd largest city in the country"). These
purposes are related to the linguistic notions of

8. What are Natural Numbers
Natural numbers have two main purposes: counting
("there are 6 coins on the table") and ordering ("this
is the 3rd largest city in the country"). These
purposes are related to the linguistic notions of

9. What are Natural Numbers

11. What Is a Whole Number

13. The term whole number does not have a Real
definition. Various authors use it in one of
the following senses:

14. The term whole number does not have a Real
definition. Various authors use it in one of
the following senses:
■ the nonnegative integers (0, 1, 2, 3, ...)

15. The term whole number does not have a Real
definition. Various authors use it in one of
the following senses:
■ the nonnegative integers (0, 1, 2, 3, ...)
■ the positive integers (1, 2, 3, ...)

16. The term whole number does not have a Real
definition. Various authors use it in one of
the following senses:
■ the nonnegative integers (0, 1, 2, 3, ...)
■ the positive integers (1, 2, 3, ...)
■ all integers (..., -3, -2, -1, 0, 1, 2, 3, ...).

17. ■ the nonnegative integers (0, 1, 2, 3, ...)
■ the positive integers (1, 2, 3, ...)
■ all integers (..., -3, -2, -1, 0, 1, 2, 3, ...).

18. ■ the positive integers (1, 2, 3, ...)
■ all integers (..., -3, -2, -1, 0, 1, 2, 3, ...).

19. ■ all integers (..., -3, -2, -1, 0, 1, 2, 3, ...).

22. What Are Integers

24. S: (n) integer, whole number (any of the natural numbers (positive or
negative) or zero) "an integer is a number that is not a fraction"

27. What is A real Number

29. In Math the real numbers may be described
informally in several different ways. The real
numbers include both rational numbers, such as
42 and −23/129, and irrational numbers, such
as pi and the square root of two; or, a real
number can be given by an infinite decimal
representation, such as 2.4871773339..., where
the digits continue in some way; or, the real
numbers may be thought of as points on an
infinitely long number line.

32. Rational Numbers

34. In Math, a rational number is any number that can be expressed as the quotient a/b of
t wo integers, with the denominator b not equal to zero. Since b may be equal to 1, every
integer corresponds to a rational number. The set of all rational numbers is usually
denoted (for quotient).

35. In Math, a rational number is any number that can be expressed as the quotient a/b of
t wo integers, with the denominator b not equal to zero. Since b may be equal to 1, every
integer corresponds to a rational number. The set of all rational numbers is usually
denoted (for quotient).
Formally each rational number corresponds to an equivalence class. The space , where ×
denotes the Product, consists of all ordered pairs (m,n) where m and n are integers with n ≠ 0.
The rational numbers are given by the quotient space where the equivalence relation is given
by (m1,n1) ~ (m2,n2) if, and only if, m1n2 - m2n1 = 0.

36. In Math, a rational number is any number that can be expressed as the quotient a/b of
t wo integers, with the denominator b not equal to zero. Since b may be equal to 1, every
integer corresponds to a rational number. The set of all rational numbers is usually
denoted (for quotient).
Formally each rational number corresponds to an equivalence class. The space , where ×
denotes the Product, consists of all ordered pairs (m,n) where m and n are integers with n ≠ 0.
The rational numbers are given by the quotient space where the equivalence relation is given
by (m1,n1) ~ (m2,n2) if, and only if, m1n2 - m2n1 = 0.
The decimal expansion of a rational number always either terminates after finitely many
digits or begins to repeat the same sequence of digits over and over. However, any repeating or
terminating decimal represents a rational number. These statements hold true not just for
base 10, but also for binary, hexadecimal, or any other integer base.

37. In Math, a rational number is any number that can be expressed as the quotient a/b of
t wo integers, with the denominator b not equal to zero. Since b may be equal to 1, every
integer corresponds to a rational number. The set of all rational numbers is usually
denoted (for quotient).
Formally each rational number corresponds to an equivalence class. The space , where ×
denotes the Product, consists of all ordered pairs (m,n) where m and n are integers with n ≠ 0.
The rational numbers are given by the quotient space where the equivalence relation is given
by (m1,n1) ~ (m2,n2) if, and only if, m1n2 - m2n1 = 0.
The decimal expansion of a rational number always either terminates after finitely many
digits or begins to repeat the same sequence of digits over and over. However, any repeating or
terminating decimal represents a rational number. These statements hold true not just for
base 10, but also for binary, hexadecimal, or any other integer base.
A real number that is not rational is called irrational. Irrational numbers include √2, π, and e.
The decimal expansion of an irrational number continues forever without repeating. Since the
set of rational numbers is countable, and the set of real numbers is uncountable, almost every
real number is irrational.

38. Formally each rational number corresponds to an equivalence class. The space , where ×
denotes the Product, consists of all ordered pairs (m,n) where m and n are integers with n ≠ 0.
The rational numbers are given by the quotient space where the equivalence relation is given
by (m1,n1) ~ (m2,n2) if, and only if, m1n2 - m2n1 = 0.
The decimal expansion of a rational number always either terminates after finitely many
digits or begins to repeat the same sequence of digits over and over. However, any repeating or
terminating decimal represents a rational number. These statements hold true not just for
base 10, but also for binary, hexadecimal, or any other integer base.
A real number that is not rational is called irrational. Irrational numbers include √2, π, and e.
The decimal expansion of an irrational number continues forever without repeating. Since the
set of rational numbers is countable, and the set of real numbers is uncountable, almost every
real number is irrational.

39. The decimal expansion of a rational number always either terminates after finitely many
digits or begins to repeat the same sequence of digits over and over. However, any repeating or
terminating decimal represents a rational number. These statements hold true not just for
base 10, but also for binary, hexadecimal, or any other integer base.
A real number that is not rational is called irrational. Irrational numbers include √2, π, and e.
The decimal expansion of an irrational number continues forever without repeating. Since the
set of rational numbers is countable, and the set of real numbers is uncountable, almost every
real number is irrational.

40. A real number that is not rational is called irrational. Irrational numbers include √2, π, and e.
The decimal expansion of an irrational number continues forever without repeating. Since the
set of rational numbers is countable, and the set of real numbers is uncountable, almost every
real number is irrational.

43. What Is A Irrational

46. A real number !at " not rational " called irrational. Irrational numbers include
√2, π, and e. &e decimal expansion of an irrational number continues forever
wi!(t repeating. Since ) set of rational numbers " c(ntable, and ) set of real
numbers " unc(ntable, almo* every real number " irrational.

47. A real number !at " not rational " called irrational. Irrational numbers include
√2, π, and e. &e decimal expansion of an irrational number continues forever
wi!(t repeating. Since ) set of rational numbers " c(ntable, and ) set of real
numbers " unc(ntable, almo* every real number " irrational.
In abstract algebra, the rational numbers form a field. This is the archetypical field of
characteristic zero, and is the field of fractions for the ring of integers. Finite
extensions of are called algebraic number fields, and the algebraic closure of is the
field of algebraic numbers.

48. A real number !at " not rational " called irrational. Irrational numbers include
√2, π, and e. &e decimal expansion of an irrational number continues forever
wi!(t repeating. Since ) set of rational numbers " c(ntable, and ) set of real
numbers " unc(ntable, almo* every real number " irrational.
In abstract algebra, the rational numbers form a field. This is the archetypical field of
characteristic zero, and is the field of fractions for the ring of integers. Finite
extensions of are called algebraic number fields, and the algebraic closure of is the
field of algebraic numbers.

49. A real number !at " not rational " called irrational. Irrational numbers include
√2, π, and e. &e decimal expansion of an irrational number continues forever
wi!(t repeating. Since ) set of rational numbers " c(ntable, and ) set of real
numbers " unc(ntable, almo* every real number " irrational.
In abstract algebra, the rational numbers form a field. This is the archetypical field of
characteristic zero, and is the field of fractions for the ring of integers. Finite
extensions of are called algebraic number fields, and the algebraic closure of is the
field of algebraic numbers.

50. In abstract algebra, the rational numbers form a field. This is the archetypical field of
characteristic zero, and is the field of fractions for the ring of integers. Finite
extensions of are called algebraic number fields, and the algebraic closure of is the
field of algebraic numbers.

53. Chart
Irrational
Rational
Integers
Whole
Natural

54. Bibliography

56. Bibliography

57. Bibliography
http://en.wikipedia.org/wiki/Natural_number

58. Bibliography
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Whole_number

59. Bibliography
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Whole_number
http://wordnetweb.princeton.edu/perl/webwn?s=integer

60. Bibliography
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Whole_number
http://wordnetweb.princeton.edu/perl/webwn?s=integer
http://en.wikipedia.org/wiki/Real_number

61. Bibliography
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Whole_number
http://wordnetweb.princeton.edu/perl/webwn?s=integer
http://en.wikipedia.org/wiki/Real_number
http://en.wikipedia.org/wiki/Rational_numbers

62. Bibliography
http://en.wikipedia.org/wiki/Natural_number
http://en.wikipedia.org/wiki/Whole_number
http://wordnetweb.princeton.edu/perl/webwn?s=integer
http://en.wikipedia.org/wiki/Real_number
http://en.wikipedia.org/wiki/Rational_numbers

63. Bibliography
http://en.wikipedia.org/wiki/Whole_number
http://wordnetweb.princeton.edu/perl/webwn?s=integer
http://en.wikipedia.org/wiki/Real_number
http://en.wikipedia.org/wiki/Rational_numbers

64. Bibliography
http://wordnetweb.princeton.edu/perl/webwn?s=integer
http://en.wikipedia.org/wiki/Real_number
http://en.wikipedia.org/wiki/Rational_numbers

65. Bibliography
http://en.wikipedia.org/wiki/Real_number
http://en.wikipedia.org/wiki/Rational_numbers

66. Bibliography
http://en.wikipedia.org/wiki/Rational_numbers

67. Bibliography

68. Bibliography