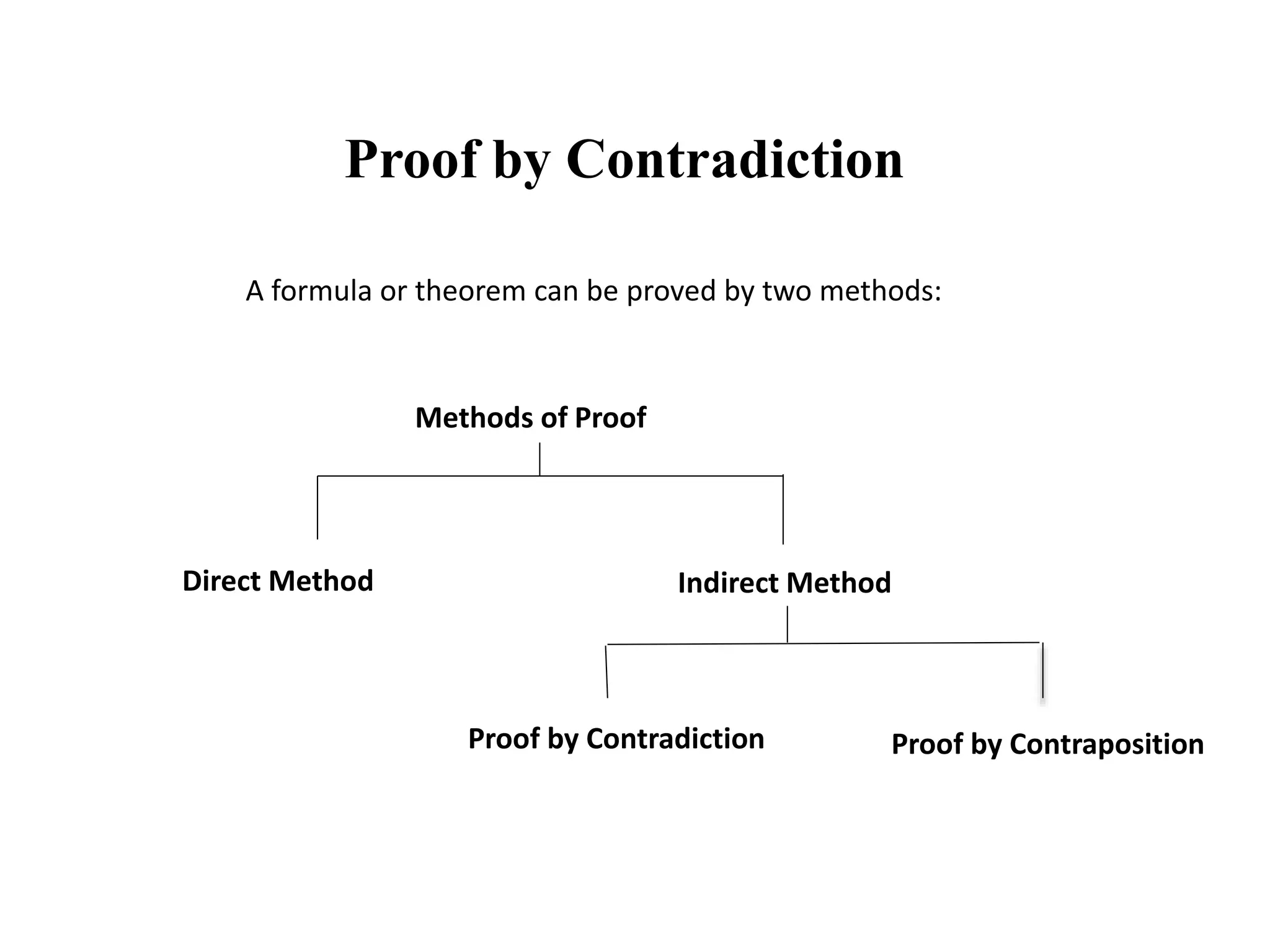
This document discusses proof by contradiction in mathematics. It begins by defining proof by contradiction as proving the truth of a statement by showing that assuming the statement is false leads to a contradiction. The document then provides examples of proofs by contradiction, including: 1) Proving there is no greatest integer by supposing there is a greatest integer N and showing that N+1 would also be an integer, contradicting that N was the greatest. 2) Proving the square root of 2 is irrational by supposing it is rational and showing this leads to a contradiction. 3) Explaining the general steps in a proof by contradiction: assume the statement is false, show this assumption leads to a contradiction, and thus

2. Proof By Contradiction
By:
M. Anas Makki
Roll No: 301
Abdul Rehman
Roll No: 334
Arslan
Roll No:315

3. Proof by Contradiction
A formula or theorem can be proved by two methods:
Methods of Proof
Direct Method Indirect Method
Proof by Contradiction Proof by Contraposition

4. Proof by Contradiction:
In Mathematics Proof by contradiction is a
technique that determines the truth value of a preposition/statement
by showing that assuming the preposition to be false.
A Proof by Contradiction is based on the fact that either a
statement is true or false but not both. Hence the supposition, that
the statement to be proved is false, leads logically to a
contradiction, impossibility or absurdity, then the supposition
must be false.

5. Steps Involved in Contradiction
1. Assume that the statement to be proved is false.
2. Show that our supposition is false.
3. In last step, we conclude that our actual statement is
true because our supposition is false.

6. Theorem:
Prove that There is no greatest integer.
Solution:
Suppose there is a greatest integer N. i.e. n ≤ N
Let M=N+1
Now, M is an integer because it is sum of two integers
Also, M>N
Hence our supposition is false that there is a greatest integer.
Therefore, it has been proved that there is no greatest integer.

7. EXERCISE:
Give a proof by contradiction for the statement:
“If n2 is an even integer then n is also an even integer.”
Proof:
Suppose n2 is even and n is not even, means n is odd.
If n is odd then :
Let n=2k+1
squaring both sides
n2 = (2k+1)2
= 4k2+4k+1
= 2(2k2+2k)+1
let r= 2k2+2k
Then n2= 2r+1 here n2 becomes odd
but we have specify at the beginning that n2 is even.
hence our supposition is false , So the statement is true.

8. Exercise:
Prove that √𝟐+ 𝟑 𝒊𝒔 𝒊𝒓𝒓𝒂𝒕𝒊𝒐𝒏𝒂𝒍.
Solution:
Let √2+ 3 is rational
Then,
√2+ 3 =
𝑎
𝑏
Squaring both sides.
2+3+2 2 3 =
𝑎2
𝑏2
5 + 2( 6 =
𝑎2
𝑏2
2 6 =
𝑎2
𝑏2 - 5
√6 =
𝑎2 − 5𝑏2
2𝑏2
Here √6 become rational but in actual it is not rational, it is a contradiction.
So the Theorem is true that √2+ 3 is a irrational.

9. EXERCISE:Prove that √2is irrational.
Solution:
let √2 is rational number. Where a, b ε Z
b ≠ 0
(also a, b are in lowest form)
√2 =
𝑎
𝑏
Squaring both sides…
2 =
𝑎2
𝑏2
2b2 = a2 _________ (1)
here a2 is even
if a2 is even then a is also even
let a = 2m __________(2)
Put a= 2m in eq. (1)
2b2 = 4m2
b2= 2m2 __________________(3)
here b2 is even
if b2 is even it means b is also even
b = 2r _________(4)
dividing (2) by (4)
𝑎
𝑏
=
2𝑚
2𝑟
Here we can see that
2𝑚
2𝑟
is not in lowest form.But
𝑎
𝑏
was in lowest form. It is a
contradiction . Hence 2𝑖𝑠 𝑖𝑟𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙.

10. Exercise:
Prove by contradiction method, the statement: If n and m are odd
integers, then n + m is an even integer.
Solution:
• In first step we suppose that n and m are odd and n + m is not
even (odd i.e. by taking contradiction).
• Now
n = 2p + 1(General form of odd) for some integer p
m = 2q + 1 for some integer q
• Adding above two equation we get,
n + m = (2p + 1) + (2q + 1)
= 2p + 2q + 2 (General Odd’s Form)
= 2· (p + q + 1) Taking two common.
This is a contradiction to our supposition, because when we
multiply 2 with odd, we get even number…..
e.g. 2(7)=14

11. EXERCISE:
Prove that if n is an integer and n3 + 5 is odd, then n is even using
contradiction method.
Solution:
• We assume that the our statement to be proved is false,
• Suppose that n3 + 5 is odd and n is not even (odd).
• Since n is odd and the product of two odd numbers is odd,
•It means that n2 is odd and
and n3 = n2 .n is also odd
•Further, since the difference of two odd number is even,
which is given
5 = (n3 + 5) – n3
Which is even.
This is a contradiction, therefore our supposition is false,
So our statement is true.

12. THEOREM:
The sum of any rational number and any irrational number is irrational.
We suppose that there is a rational number r and an irrational number s
such that r + s is rational.
as r is a rational
So r =
𝑎
𝑏
r + s =
𝑐
𝑑
_____________(2)
put r =
𝑎
𝑏
in equation .. 2
𝑎
𝑏
+ s =
𝑐
𝑑
s =
𝑐
𝑑
-
𝑎
𝑏
s =
𝑏𝑐 −𝑎𝑑
𝑏𝑑
Here s is become rational but we have assumed that s is irrational. It is a
contradiction. So the theorem has been proved.

13. Exercise:
Prove by contradiction that 6 − 7 is irrational
Proof:
•Since a, b are integers
•And is the quotient of two integers.
• , then is irrational , which shows that our supposition is false, so
given statement is true.
2
2
2

14. Proof By CONTRAPOSITIVE
What is CONTRAPOSITIVE?
The contra-positive of the conditional statement p → q is
~ q → ~ p.
A conditional and its contra-positive are equivalent.
Symbolically p → q ≡ ~q → ~p
For example a contra-positive of a conditional statement is,
• If today is Friday, then 2 + 3 = 5.
The contra-positive of the above statement will be,
•If 2 + 3 ≠ 5, then today is not Friday.
We can see that these above two statement are logically equivalent to each
others.

15. STEPS INVOLVED PROOF BY CONTRAPOSITION
1. Express the statement in the form if p then q.
2. Rewrite this statement in the contra-positive form,
if not q then not p
3. Prove the contra-positive by a direct proof.

16. EXERCISE:
Prove that for all integers n, if n2 is even then n is even.
SOLUTON:
•First we write then the contra-positive of the given
statement,
“if n is not even (odd) then n2 is not even (odd)”
•Now prove the contra-positive directly.
•Suppose n is odd, which means
n=2k+1 [General form of Odd]
•Now take the square root of n,
n2 =(2k+1)2
n2 = 4k2 +4k+1
= 2·(2k 2 + 2k) + 1
• = 2·r + 1 [where r = 2k2 + 2k € Z]
Hence n2 is odd and both statements are true. Thus the
contra-positive statement is true and so the given
statement is true.

17. EXERCISE:
Prove that if 3n + 2 is odd, then n is odd.
SOLUTON:
The contra-positive of the given conditional statement is,
“ if n is even then 3n + 2 is even”
Lets us assume that n is even which means,
n=2k [By the definition of even]
Also 3n+2 is also even, so
3n+2= 3(2k)+2 [using the value of n]
= 6k + 2
= 2(3k+1)
= 2.r where r = (3k + 1) € Z
Hence 3n + 2 is even. We conclude that the given statement is true
since its contra-positive is true.

18. EXERCISE:
Prove that if n is an integer and n3 + 5 is odd, then n is even.
Solution:
•First we write the contra-positive of the statement,
“n is odd and n3 + 5 is even.”
Suppose n is an odd integer. Since, a product of two odd
integers is odd, therefore
n2 = n.n is also odd.
then n3 = n2.n is also odd.
Further since the sum of two odd number is even,
For example,
9+3=12 (Which is even)
So,
n3 +5 will also be even.
Thus we have prove that if n is odd then n3 + 5 is even.
So our statement will also be true.

19. THE END