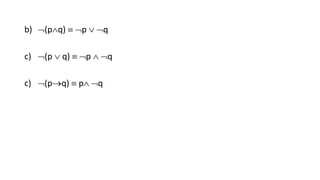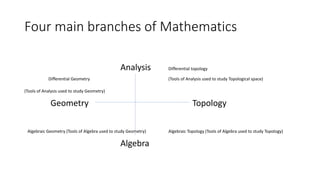
This document provides an introduction to mathematical analysis by outlining key topics including: - An overview of analysis and its focus on real-valued functions of a single real variable and their analytic properties like limits, continuity, and differentiability. - A review of logic including definitions of statements, connectives, implications, and equivalences. - An introduction to proof, discussing the difference between conjectures, theorems, lemmas, and corollaries and how proofs demonstrate statements are universally true or find counter examples.

1. Welcome

2. INTRODUCTION TO
MATHEMATICAL ANALYSIS

3. TOPICS
•Brief Overview of Analysis
•Review of Logic
•Introduction to Proof

4. Overview of Analysis
• Analysis is the study of functions, especially those representing
continuous change in a particular space.
Example
Real coordinate space – Domain of Real Analysis
Complex coordinate space – Domain of Complex Analysis
Arbitrary Vector Space – Domain of Functional Analysis

5. • We will focus on real-valued functions of a single real variable.
Example
f : R R
Analysis focuses on analytic properties of functions.
Example
Limits, Continuity, Differentiability, Smoothness, Integrability,
Convergence, Analyticity, Measurability.

6. • Historically, Calculus preceded Analysis. Analysis began as an effort to
establish a strong theoretical foundation for calculus.
• Modern analysis is part of the core theoretical framework for many
fields of Mathematics.
Example
ODEs, PDEs, Probability Theory, Analytic Number Theory, Ergotic
Theory, Optimization Theory, etc.

7. Four main branches of Mathematics
Analysis Differential topology
Differential Geometry (Tools of Analysis used to study Topological space)
(Tools of Analysis used to study Geometry)
Geometry Topology
Algebraic Geometry (Tools of Algebra used to study Geometry) Algebraic Topology (Tools of Algebra used to study Topology)
Algebra

8. Introduction to Real analysis needs some concepts from Topology such
as open/closed sets and compactness.

9. Review of Logic
• Definition
A statement is a sentence that is either true or false, but not
both.
Example
a) “Every continuous function is differentiable”
This is a false statement.
b) “The set of integers is countable”
This is a true statement.

10. • c) “𝑥2 − 5𝑥 + 6 = 0”
This is not a statement since it is both true and false depending
upon x.
If x = 2 or 3 , then it is true, otherwise, it is false.
“𝑥2 − 5𝑥 + 6 = 0 whenever x = 2” is a statement.
Statements can be combined with connectives:
and , or, if … then , if and only if

11. Definition
• A statement without a connective is called a prime statement. A
statement with a connective is called a composite statement.
• Let p be a statement. The negation of p is the logical opposite of p
and is denoted  p (read “not p”).
p  p
T F
F T

12. Example
a) p : Every continuous function is differentiable.
 p : Not every continuous function is differentiable.
b) P : The set of integers is countable.
 p : The set of integers is not countable
or The set of integers is uncountable

13. Definition
• Let p and q be statements. The statement “p and q” is called the
conjunction of p and q and is denoted pq . pq is true precisely
when both p and q are true and is false otherwise.
p q pq
T T T
T F F
F T F
F F F

14. Definition
• Let p and q be statements. The statement “p or q” is called
disjunction of p and q and is denoted pq . pq is false precisely
when both p and q are false and is true otherwise.
p q p  q
T T T
T F T
F T T
F F F

15. Definition
• A statement of the form “if p then q” is called an implication or a
conditioned statement and is denoted pq. In an implication pq,
p is called the antecedent or hypothesis while q is called the
consequent or conclusion.
• An implication pq is false precisely when the hypothesis is true and
the conclusion is false.
p q p  q
T T T
T F F
F T T
F F T

16. • The cases for which the hypothesis is false are called vacuously true
cases.
An implication pq can be written in several ways:
if p, then q
p implies q
q if p
q whenever p
q provided that p

17. Definition
• The converse of an implication pq is qp. The contrapositive of an
implication pq is q  p . The inverse of an implication p q is
p  q .
• A statement of the form “p if and only if q” is called an equivalence or
biconditional statement and is denoted pq. pq is true precisely
when p and q have the same truth values.
p q p  q
T T T
T F F
F T F
F F T

18. • The phrase “if and only if” is abbreviated iff.
• A definition, whether stated as such or not, is always a biconditional
statement.
A statement that is true in all cases is called a tautology. A statement
that is false in all cases is called a contradiction.
Two statements composed of the same prime statements are logically
equivalent iff their truth tables are identical or, equivalently, iff the
biconditional joining them is a tautology.

19. Examples
a) pq  (pq)(qp)
p q (pq)(qp) pq
T T T T T T
T F F F T F
F T T F F F
F F T T T T

20. b) (pq)  p  q
c) (p  q)  p  q
c) (pq)  p q

21. Introduction to Proof
Definitions
An assertion (claim) that is still to be proved or refuted is called a conjecture.
An assertion that has been proved is called a theorem.
Lemmas and corollaries are special types of theorem.
A lemma is a theorem that is used primarily in the proof of a more general
theorem in order to simplify the proof and to make the proof more
straightforward.
A corollary is a theorem that can be stated as a special case of a more
general theorem.
Theorems build upon lemmas and tend toward increasing generality while
corollaries follow from more general theorems and tend toward increasing
specificity.

22. • To prove a conjecture, we must demonstrate that it is true for every
case.
• To refute a conjecture, we need only find one example where it is
false, such an example is called a counter example.
• Many theorems in Mathematics take the form of an implication pq.
• To prove an implication, we assume p is true and show that q is also.
• To refute the claim that pq is true in every case, we show pq is
true in at least one example.
So we need an example where p is true and q is false.

23. Thank you