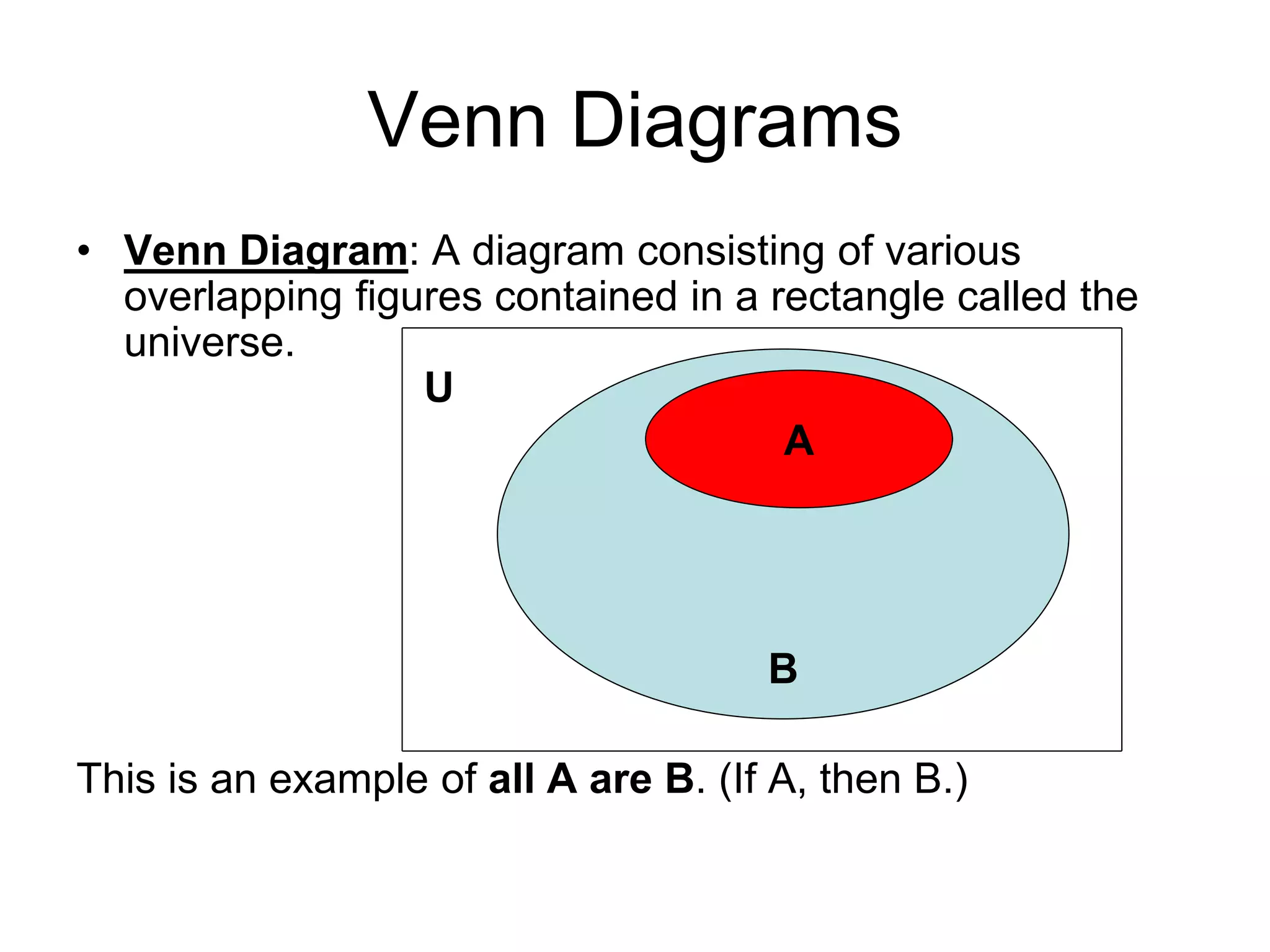
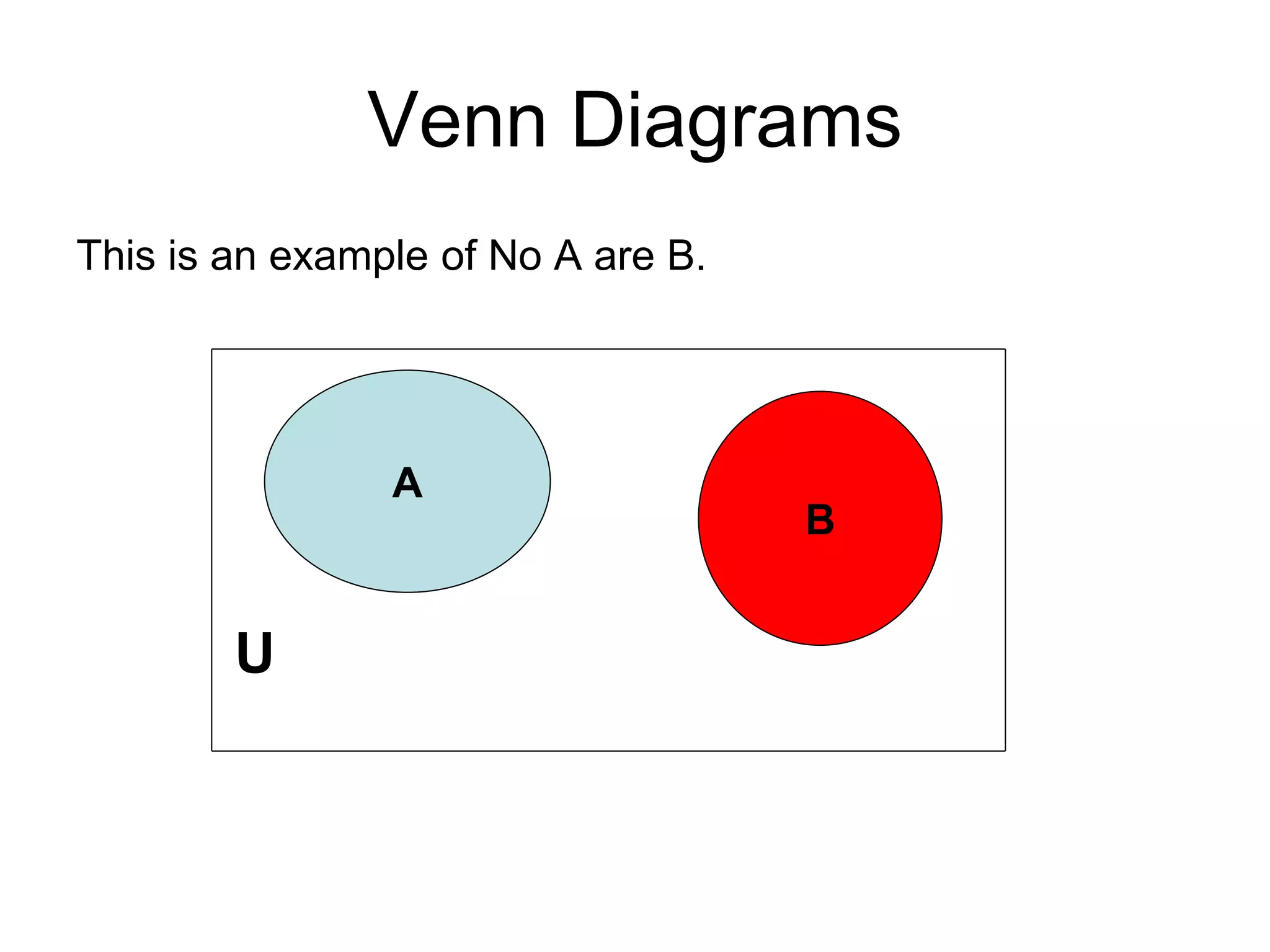
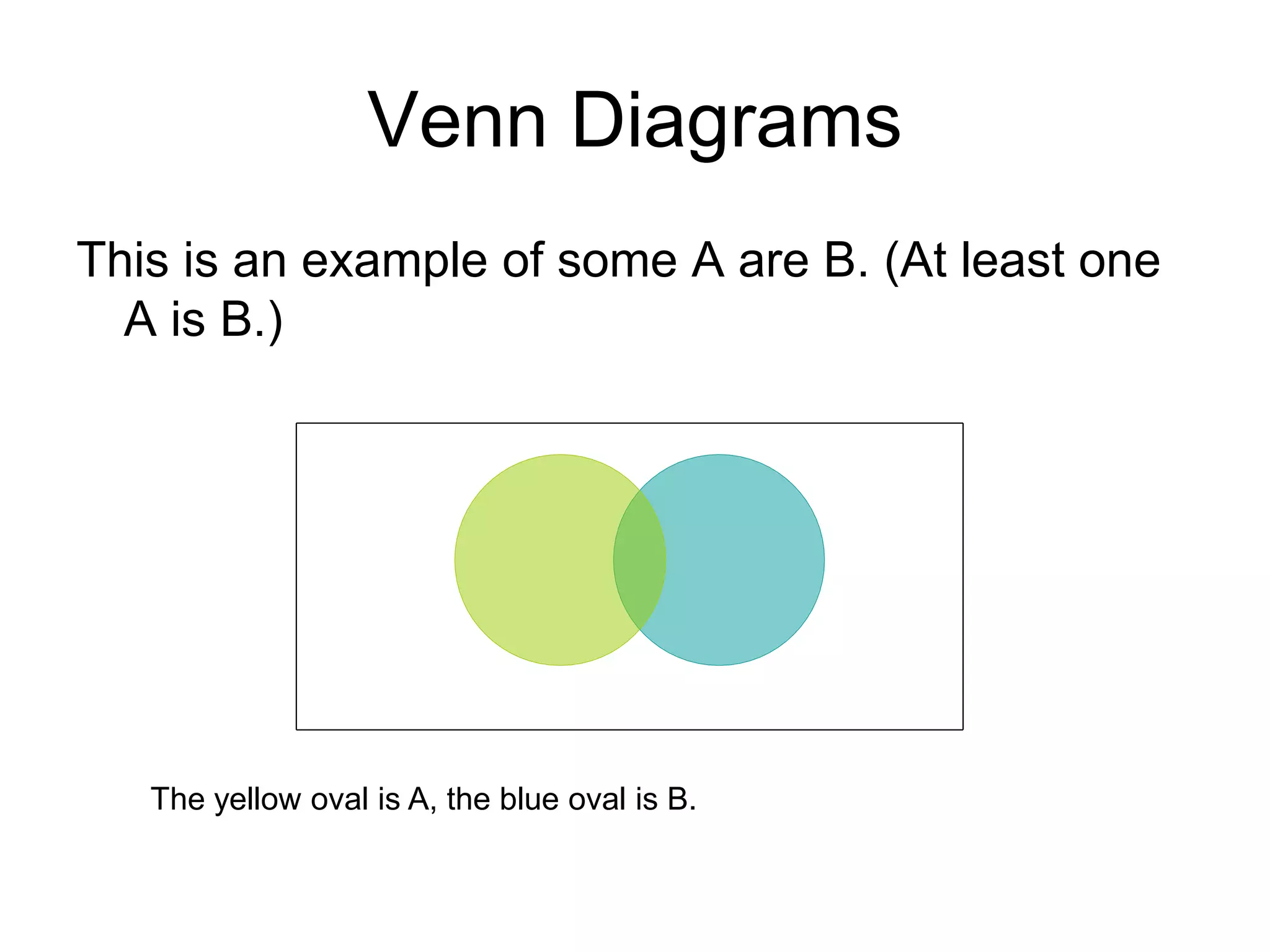
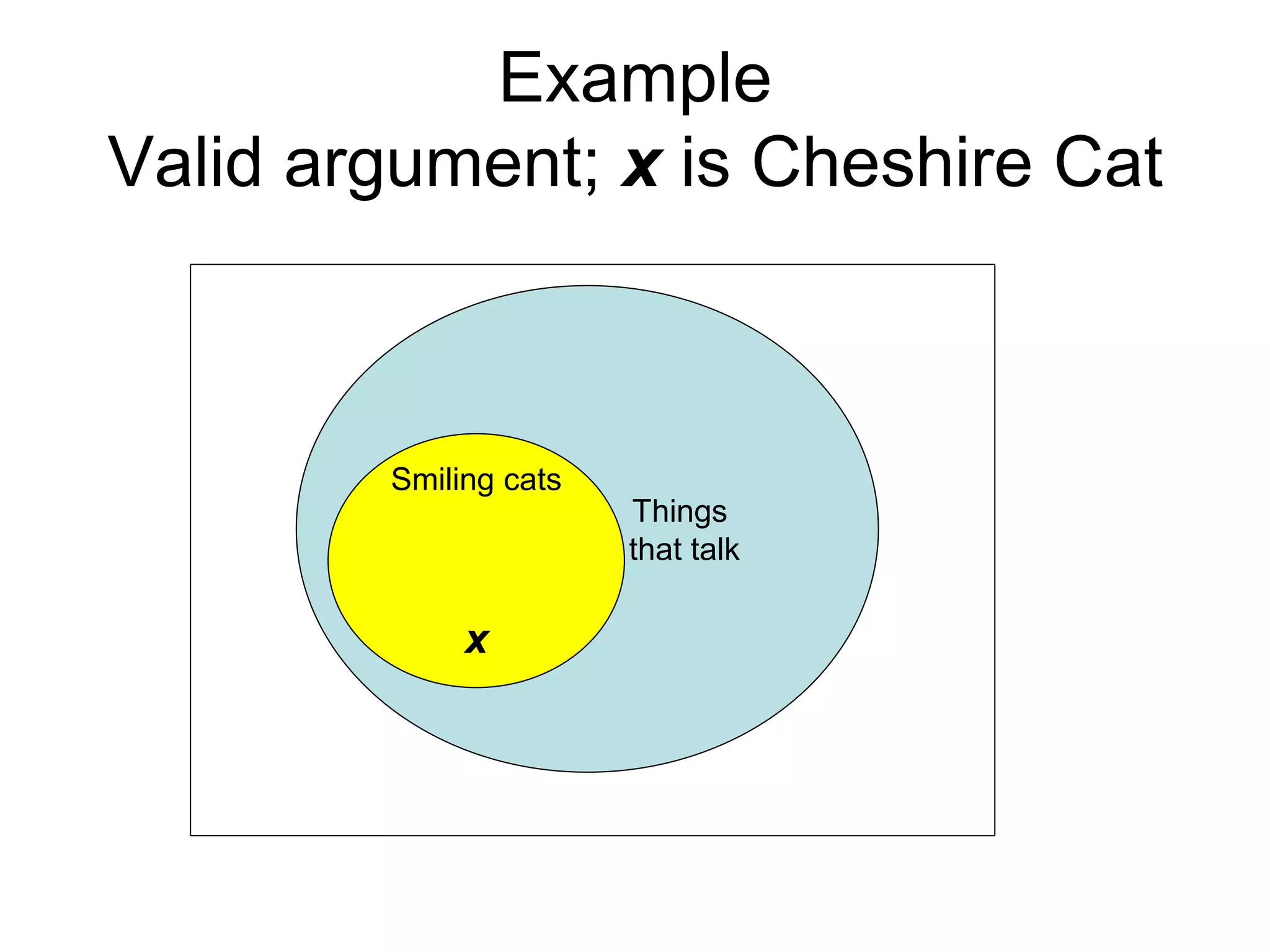
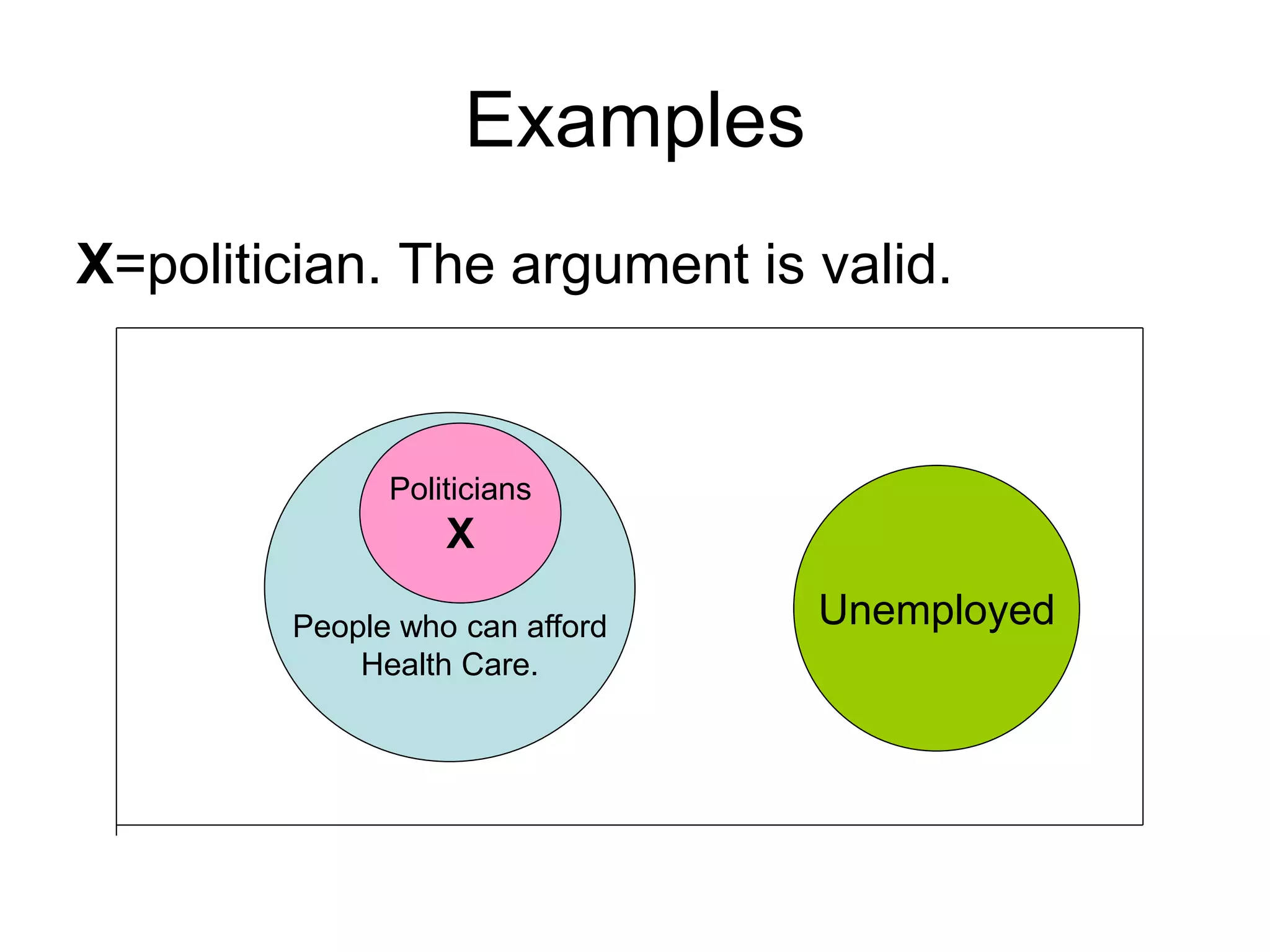
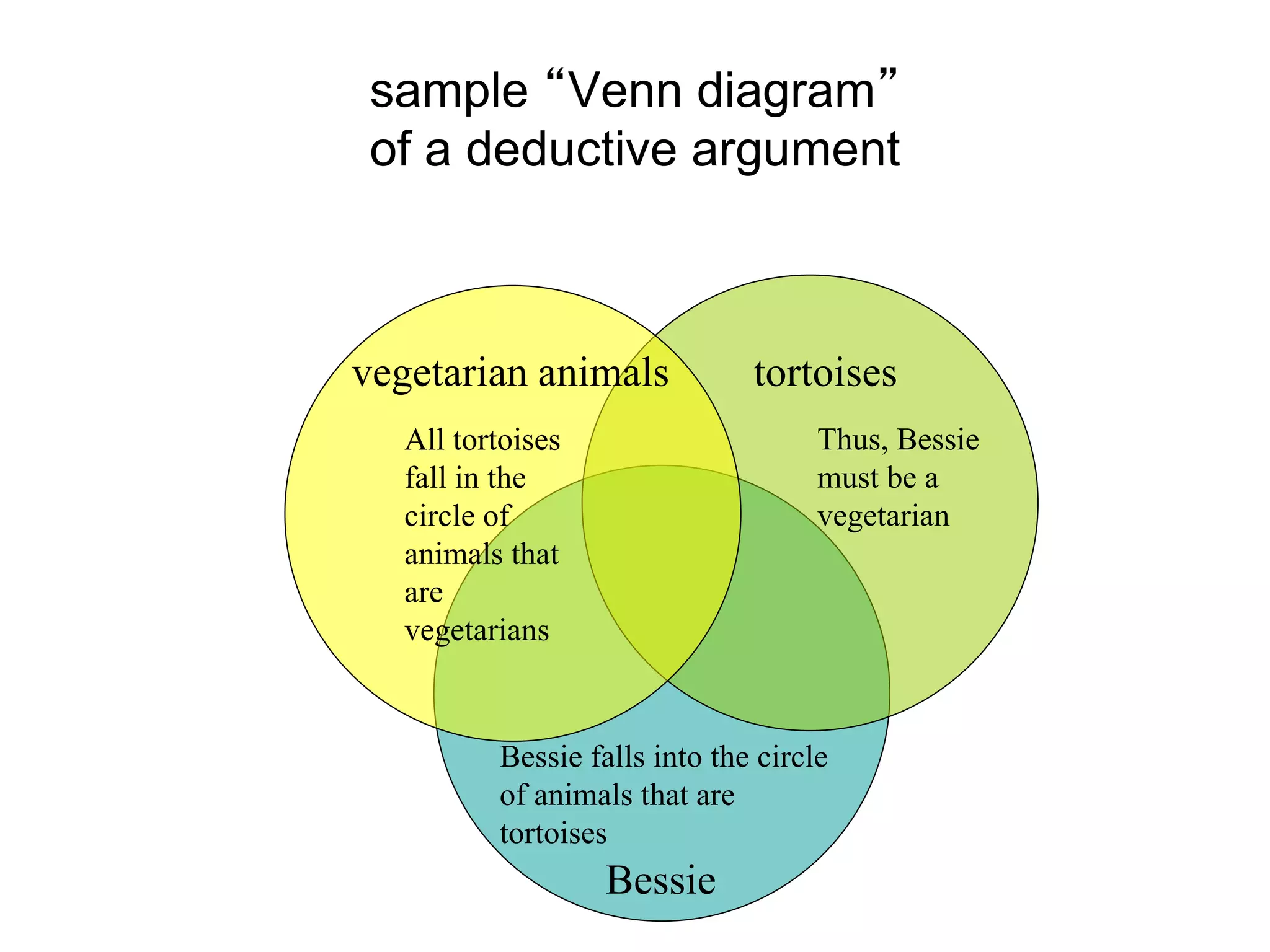
The document differentiates between deductive and inductive reasoning, explaining that deductive reasoning moves from general premises to specific conclusions, while inductive reasoning moves from specific instances to general conclusions. It emphasizes the validity of deductive arguments, which require the truth of premises for soundness, and the uncertain but probable nature of inductive arguments. The document also provides examples of both reasoning types and mentions their applications in various fields.

1. DEDUCTIVE vs. INDUCTIVE
REASONING

2. Problem Solving
• Logic – The science of correct reasoning.
• Reasoning – The drawing of inferences or
conclusions from known or assumed facts.
When solving a problem, one must
understand the question, gather all
pertinent facts, analyze the problem i.e.
compare with previous problems (note
similarities and differences), perhaps use
pictures or formulas to solve the problem.

3. Deductive Reasoning
• Deductive Reasoning – A type of logic in
which one goes from a general statement
to a specific instance.
• The classic example
All men are mortal. (major premise)
Socrates is a man. (minor premise)
Therefore, Socrates is mortal. (conclusion)
The above is an example of a syllogism.

4. Deductive Reasoning
• Syllogism: An argument composed of two
statements or premises (the major and minor
premises), followed by a conclusion.
• For any given set of premises, if the conclusion
is guaranteed, the arguments is said to be valid.
• If the conclusion is not guaranteed (at least one
instance in which the conclusion does not
follow), the argument is said to be invalid.
• BE CARFEUL, DO NOT CONFUSE TRUTH
WITH VALIDITY!

5. Deductive Reasoning
Examples:
1. All students eat pizza.
Claire is a student at ASU.
Therefore, Claire eats pizza.
2. All athletes work out in the gym.
Barry Bonds is an athlete.
Therefore, Barry Bonds works out in the gym.

6. Deductive Reasoning
3. All math teachers are over 7 feet tall.
Mr. D. is a math teacher.
Therefore, Mr. D is over 7 feet tall.
• The argument is valid, but is certainly not true.
• The above examples are of the form
If p, then q. (major premise)
x is p. (minor premise)
Therefore, x is q. (conclusion)

7. Venn Diagrams
• Venn Diagram: A diagram consisting of various
overlapping figures contained in a rectangle called the
universe.
U
This is an example of all A are B. (If A, then B.)
B
A

8. Venn Diagrams
This is an example of No A are B.
U
A
B

9. Venn Diagrams
This is an example of some A are B. (At least one
A is B.)
The yellow oval is A, the blue oval is B.

10. Example
• Construct a Venn Diagram to determine
the validity of the given argument.
#14 All smiling cats talk.
The Cheshire Cat smiles.
Therefore, the Cheshire Cat talks.
VALID OR INVALID???

11. Example
Valid argument; x is Cheshire Cat
Things
that talk
Smiling cats
x

12. Examples
• #6 No one who can afford health
insurance is unemployed.
All politicians can afford health
insurance.
Therefore, no politician is unemployed.
VALID OR INVALID?????

13. Examples
X=politician. The argument is valid.
People who can afford
Health Care.
Politicians
X
Unemployed

14. Example
• #16 Some professors wear glasses.
Mr. Einstein wears glasses.
Therefore, Mr. Einstein is a professor.
Let the yellow oval be professors, and the blue oval be glass
wearers. Then x (Mr. Einstein) is in the blue oval, but not in the
overlapping region. The argument is invalid.

15. Inductive Reasoning
Inductive Reasoning, involves going from a
series of specific cases to a general
statement. The conclusion in an inductive
argument is never guaranteed.
Example: What is the next number in the
sequence 6, 13, 20, 27,…
There is more than one correct answer.

16. Inductive Reasoning
• Here’s the sequence again 6, 13, 20, 27,…
• Look at the difference of each term.
• 13 – 6 = 7, 20 – 13 = 7, 27 – 20 = 7
• Thus the next term is 34, because 34 – 27 = 7.
• However what if the sequence represents the
dates. Then the next number could be 3 (31 days
in a month).
• The next number could be 4 (30 day month)
• Or it could be 5 (29 day month – Feb. Leap year)
• Or even 6 (28 day month – Feb.)

17. Two basic categories
of human reasoning
• Deduction: reasoning from general premises, which are
known or presumed to be known, to more specific, certain
conclusions.
• Induction: reasoning from specific cases to more general,
but uncertain, conclusions.
• Both deductive and inductive arguments occur frequently
and naturally…both forms of reasoning can be equally
compelling and persuasive, and neither form is preferred
over the other (Hollihan & Baske, 1994).

18. Deduction Vs. Induction
Deduction:
• commonly associated
with “formal logic.”
• involves reasoning
from known premises,
or premises presumed
to be true, to a certain
conclusion.
• the conclusions
reached are certain,
inevitable,
inescapable.
Induction
• commonly known as
“informal logic,” or
“everyday argument”
• involves drawing
uncertain inferences,
based on probabalistic
reasoning.
• the conclusions
reached are probable,
reasonable, plausible,
believable.

19. Deductive Versus
Inductive Reasoning
Deduction
• It is the form or structure
of a deductive argument
that determines its validity
• the fundamental property
of a valid, deductive
argument is that if the
premises are true, then
the conclusion necessarily
follows.
• The conclusion is said to
be “entailed” in, or
contained in, the premises.
– example: use of DNA
testing to establish
paternity
Induction
• By contrast, the form or
structure of an inductive
argument has little to do with
its perceived believability or
credibility, apart from making
the argument seem more
clear or more well-organized.
• The receiver (or a 3rd party)
determines the worth of an
inductive argument

20. Sample Deductive and Inductive Arguments
Example of
Deduction
• major premise: All
tortoises are
vegetarians
• minor premise:
Bessie is a tortoise
• conclusion:
Therefore, Bessie
is a vegetarian
Example of
Induction
• Boss to employee:
“Biff has a tattoo of an
anchor on his arm. He
probably served in the
Navy.”

21. Bessie
tortoises
vegetarian animals
sample “Venn diagram”
of a deductive argument
All tortoises
fall in the
circle of
animals that
are
vegetarians
Bessie falls into the circle
of animals that are
tortoises
Thus, Bessie
must be a
vegetarian

22. Deduction Versus Induction
---continued
• Deductive
reasoning is either
“valid” or “invalid.”
A deductive
argument can’t be
“sort of” valid.
• If the reasoning
employed in an
argument is valid
and the argument’s
premises are true,
then the argument is
said to be sound.
valid reasoning
+ true premises
= sound
argument
• Inductive reasoning
enjoys a wide range of
probability; it can be
plausible, possible,
reasonable, credible,
etc.
• the inferences drawn
may be placed on a
continuum ranging from
cogent at one end to
fallacious at the other.
fallacious cogent

23. Deduction Versus Induction
--still more
• Deductive reasoning is
commonly found in the
natural sciences or
“hard” sciences, less so
in everyday arguments
• Occasionally, everyday
arguments do involve
deductive reasoning:
Example: “Two or more
persons are required to
drive in the diamond
lane. You don’t have
two or more persons.
Therefore you may not
drive in the diamond
lane”
• Inductive reasoning is
found in the courtroom,
the boardroom, the
classroom, and
throughout the media
• Most, but not all everyday
arguments are based on
induction
– Examples: The
“reasonable person”
standard in civil law, and
the “beyond a
reasonable doubt”
standard in criminal law

24. all rectangles are squares.
abcd is a square.
so,abcd is a rectangle.
is this valid?