Embed presentation







This document provides an introduction to integration, which is the inverse process of differentiation. It discusses the basic notation and concepts of integration, such as taking the integral of a function to find its anti-derivative and adding a constant C. Examples are provided of integrating common functions and determining the constant value based on initial conditions. Questions and answers about integration techniques are also presented.
Overview of integration as the inverse of differentiation. Focus on integration notation and process.
Introduction to indefinite integration with the formula for integrating power functions.
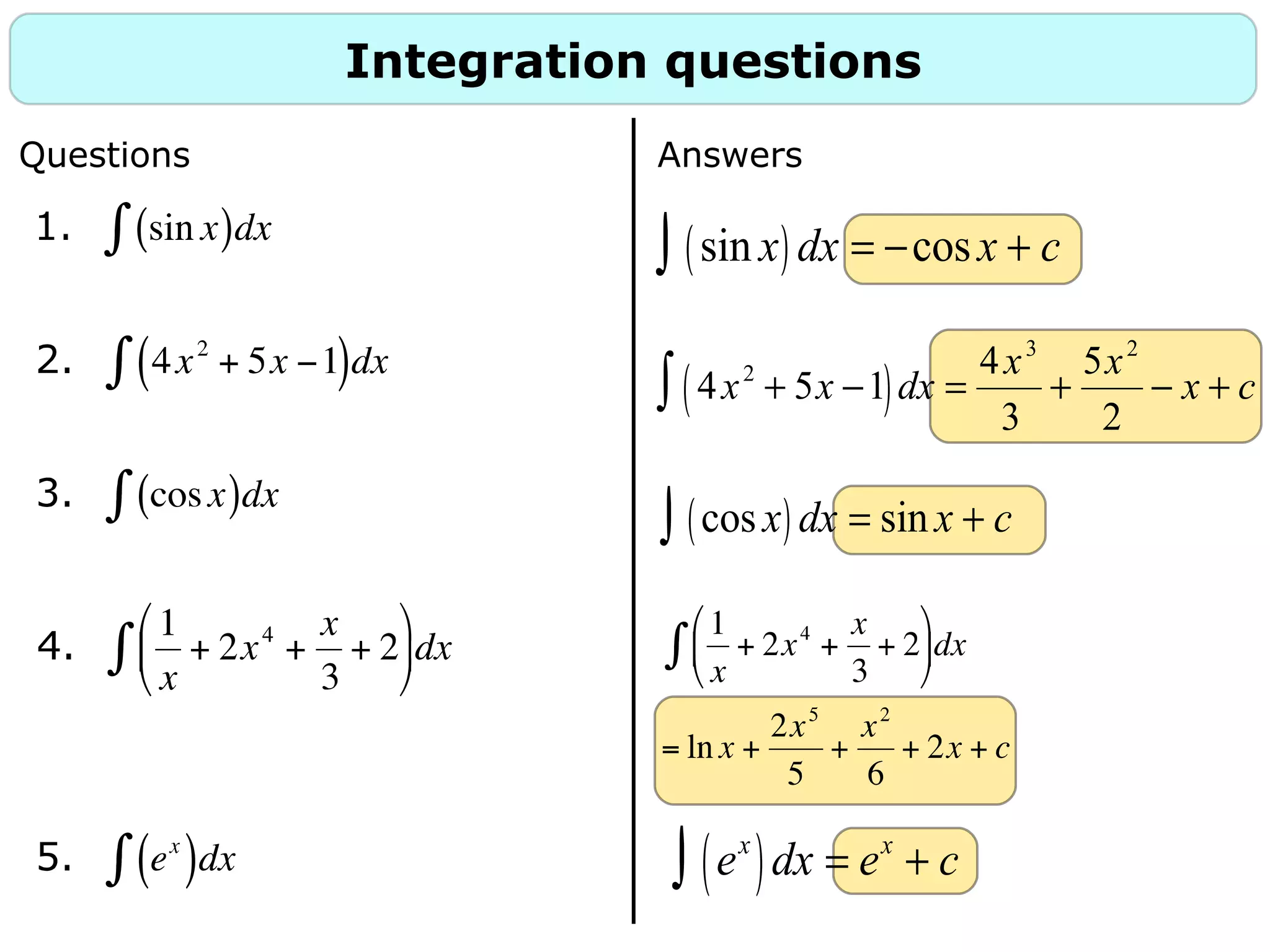
Presentation of integration questions, providing solutions for various functions including trigonometric and exponential.
Integration involves rewriting functions for simpler integration, including worked examples.
Determining the constant term 'c' in polynomial functions by using specific points for evaluation.







