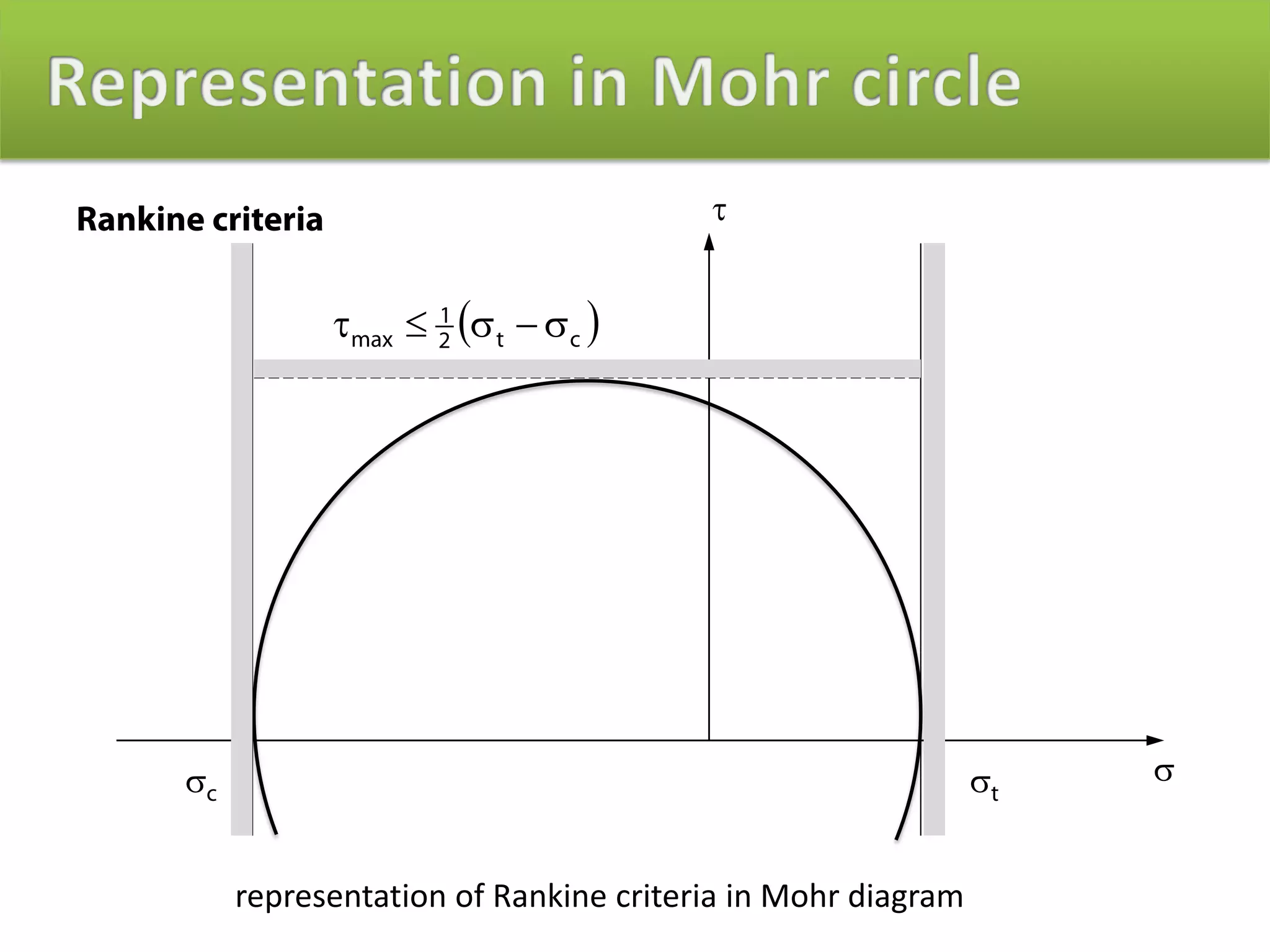
The document discusses different stress and failure criteria used to analyze materials. It describes the Tresca, Von Mises, and Rankine criteria, which use maximum shear stress, equivalent deviatoric strain energy, and limits on principal stresses respectively to determine failure. The Von Mises criterion applies best to isotropic ductile metals, while Tresca and Rankine criteria can also be used for such materials. Rankine is more suitable for low-cohesion materials like ceramics. The appropriate criterion depends on the material properties.

1. Stress
Measures and Failure Criteria
Alan Ho
08 February 2010

2. Stress tensor: principal components
By calculating its eigen-values & eigen-vectors, the stress tensors can be
written in its principal coordinate system in a purely diagonal form
containing only normal stress components which are called the principal
stress components. The eigenvectors of σ determine the orientation of the
principal coordinate system ê1,2,3 and thus of the principal stress directions :
σ1 0 0
σê =  0 σ2
 0 
1, 2 , 3
0 0
 σ3 

The principal stresses are also one set of invariants of the stress tensor.
Conventionally, the principal stresses σ1, σ2 and σ3 are ordered such that:
σ1 > σ2 > σ3

3. Stress tensor decomposition: hydrostatic - deviatoric parts
The stress tensor can be divided in hydrostatic and deviatoric part:
σ = σh + σ = pl + ~
~ σ
Where p = 3 σ ii is the hydrostatic pressure and ~ is called the deviatoric stress tensor.
1
σ
Strain energy decomposition
Using the hydrostatic - deviatoric stress & strain decomposition, the strain
energy can be written as:
~
E = 2 σ : ε = 2 σh : ε h + 2 σ : ~ = E h + E
1 1 1~
ε

4. Tresca equivalent stress criteria
The Tresca stress criteria is based on the comparison of maximum shear τmax
and is thus defined basically from the maximum principal stress difference :
σ eq = max( σ1 − σ2 , σ2 − σ3 , σ3 − σ1 )
tresca
The corresponding yield / failure criteria is simply written as a comparison
with the maximum allowed shear stress τy or from a uniaxial stress state
σ y : σ eq ≤ 2τ y = σ y
tresca
Postulates that yielding occur when the maximum shearing stress at a
particle of a body in a general, triaxial state of stress attains a value equal to
the maximum shearing stress at yielding in uniaxial tension.
Also known as the maximum shear stress criterion.

5. Tresca criteria τ
τmax = 2 (σ1 − σ3 ) ≤ τ y
1
σ3 σ1 σ
representation of Tresca criteria in Mohr diagram

6. Rankine stress criteria
The Rankine stress criteria simply imposes that the principal stress
components are bounded between σc (compression) and σt (tension) :
σ c < σi < σ t ∀i = 1,2,3
As a result, the maximum shear stress is also bounded: τmax ≤ 1
2 (σ t − σc )

7. Rankine criteria τ
τmax ≤ 2 (σ t − σ c )
1
σc σt σ
representation of Rankine criteria in Mohr diagram

8. Von Mises equivalent stress criteria
The Von Mises equivalent stress criteria is based on a comparison of maximum
~
deviatoric strain energy E and is thus defined from the deviatoric stress tensor ~ :
σ
σmises =
eq 3 ~:~
σ σ
2
It can also be written directly from the principal stresses σ1,2,3 or from the
stress tensor components:
(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1 )2
σ eq
mises = 2
(σ11 − σ22 )2 + (σ22 − σ33 )2 + (σ33 − σ11 )2 + 6 (σ12 − σ2 + σ2 )
2
= 2
23 31
The corresponding yield / failure criteria is simply written as a comparison
with the maximum allowed uniaxial stress y (yield stress):
σmises ≤ σ y
eq

9. 3D representation of Von Mises & Tresca yield surfaces

10. 2D representation of Von Mises & Tresca yield surfaces

11. Between Von Mises and Tresca Yield Criteria
• The Von Mises yield criterion is non-linear. whereas the Tresca yield
criterion is piecewise linear.
• However, if the ordering of the magnitudes of the principal components
of stress is not known, the Tresca yield surface involves singularities
(edges and corners) and is difficult to handle.

12. Stress criteria
• Use Von Mises criteria for isotropic, dense & ductile materials like metals which
failure does not depend on hydrostatic pressure.
• Von Mises criterion also gives a reasonable estimation of fatigue failure,
especially in cases of repeated tensile and tensile-shear loading
• Tresca criteria is more conservative than Von Mises, it is also valid for isotropic &
ductile materials and is also independent of hydrostatic pressure.
• Both Tresca & Mises criteria impose that the material has the same limit in
traction & compression. If not, consider another criteria or take the lowest limit
for safety.
• Rankine criteria is more suitable to low cohesion materials like ceramics where
the tension limit is significantly lower than the compression. In this case, you
should also check that the maximum shear (Tresca) is also below the admissible
values.
• Complex materials like concrete, ceramics, composites require much more
complex criteria taking into account the hydrostatic pressure, the
tension/compression asymmetry or the anisotropy of the material.