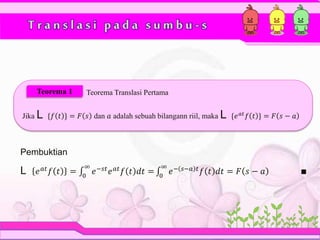
1. Teorema translasi pertama dan kedua menjelaskan bagaimana transformasi Laplace dari suatu fungsi akan berubah jika ada translasi pada sumbu waktu (t) atau frekuensi (s). 2. Teorema translasi pertama menyatakan bahwa jika terjadi translasi pada sumbu s, grafik transformasi Laplace akan bergeser sejauh nilai translasi pada sumbu s. 3. Teorema translasi kedua menyatakan bahwa jika terj

1. 10 Desember 2014
Persamaan Diferensial

2. Teorema Translasi Pertama
Jika L {𝑓 𝑡 } = 𝐹 𝑠 dan 𝑎 adalah sebuah bilangann riil, maka L {𝑒 𝑎𝑡
𝑓 𝑡 } = 𝐹 𝑠 − 𝑎
Teorema 1
Pembuktian
L 𝑒 𝑎𝑡 𝑓 𝑡 = 0
∞
𝑒−𝑠𝑡 𝑒 𝑎𝑡 𝑓 𝑡 𝑑𝑡 = 0
∞
𝑒− 𝑠−𝑎 𝑡 𝑓 𝑡 𝑑𝑡 = 𝐹 𝑠 − 𝑎 ∎
T r a n s l a s i p a d a s u m b u - s

3. T r a n s l a s i p a d a s u m b u - s
Jika kita misalkan 𝑠 adalah bilangan riil, maka grafik
dari 𝐹(𝑠 − 𝑎) adalah grafik dari 𝐹(𝑠) yang bergeser
pada sumbu 𝑠 sepanjang |𝑎|. Jika 𝑎 > 0, grafik dari
𝐹(𝑠) bergeser sepanjang 𝑎 satuan ke kanan,
kemudian jika 𝑎 < 0 grafik bergeser sepanjang 𝑎
satuan ke kiri. Lihat gambar disamping.
Lebih jelasnya dapat dituliskan dalam bentuk seperti dibawah ini.
L 𝑒 𝑎𝑡
𝑓 𝑡 = L 𝑓 𝑡 | 𝑠→𝑠−𝑎
Dimana 𝑠 → 𝑠 − 𝑎 berarti transformasi laplace 𝐹(𝑠) dari 𝑓(𝑡) dengan mengganti
simbol 𝑠 menjadi 𝑠 − 𝑎.

4. T r a n s l a s i p a d a s u m b u - s
Contoh
Tentukan : 𝑎 L {𝑒5𝑡
𝑡3
} (𝑏) L {𝑒−2𝑡
cos 4 𝑡}.
Penyelesaian
𝑎 L 𝑒 𝑎𝑡
𝑓 𝑡 = L 𝑓 𝑡 𝑠→𝑠−𝑎
L 𝑒5𝑡
𝑡3
= L 𝑡3
| 𝑠→𝑠−5
=
3!
𝑠3+1 | 𝑠→𝑠−5
=
3!
𝑠4 | 𝑠→𝑠−5
=
6
𝑠−5 4
(𝑏) L 𝑒 𝑎𝑡
𝑓 𝑡 = L 𝑓 𝑡 𝑠→𝑠−𝑎
L 𝑒−2𝑡
cos 4 𝑡 = L {cos 4𝑡}| 𝑠→𝑠− −2
=
𝑠
𝑠2 + 42
| 𝑠→𝑠+2
=
𝑠
𝑠2 + 16
| 𝑠→𝑠+2
=
𝑠 + 2
(𝑠 + 2)2+16

5. T r a n s l a s i p a d a s u m b u - t
Unit step function (fungsi tangga satuan)
didefinisikan sebagai
𝑢 𝑎 𝑡 = 𝑢 𝑡 − 𝑎 =
0, 0 ≤ 𝑡 < 𝑎
1, 𝑡 ≥ 𝑎
Perhatikan bahwa fungsi tangga satuan
𝑢 𝑡 − 𝑎 ini dapat diinterpretasikan
sebagai kondisi menekan tombol switch
on dari suatu alat elektronik pada waktu
𝑡 = 𝑎 . Saat 𝑡 < 𝑎 fungsi tersebut
bernilai 0 , sehingga merepresentasikan
kondisi alat belum dinyalakan, saat 𝑡 ≥
𝑎 fungsi bernilai 1 , dan
merepresentasikan kondisi alat sudah
menyala.
Gambar fungsi tangga satuan

6. T r a n s l a s i p a d a s u m b u - t
Teorema Translasi Kedua
Jika 𝐹(𝑠) = L {𝑓(𝑡)} dan 𝑎 > 0, maka L { 𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎 } = 𝑒−𝑎𝑠
𝐹(𝑠)
Teorema 2
Pembuktian
Dengan menggunakan sifat penjumlahan dalam integral
0
∞
𝑒−𝑠𝑡
f t − a 𝑢(𝑡 − 𝑎)𝑑𝑡, dapat ditulis menjadi 2 integral:
L 𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎 = 0
∞
𝑒−𝑠𝑡
𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎 𝑑𝑡 + 0
∞
𝑒−𝑠𝑡
𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎 𝑑𝑡
=
0
∞
𝑒−𝑠𝑡 𝑓(𝑡 − 𝑎) 𝑑𝑡
Sekarang kita misalkan 𝑣 = 𝑡 − 𝑎, 𝑑𝑣 = 𝑑𝑡 pada integral terakhir, maka
L {𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎 } = 0
∞
𝑒−𝑠 𝑣+𝑎 f 𝑣 𝑑𝑣 = 𝑒−𝑎𝑠
0
∞
𝑒−𝑠𝑣 𝑓(𝑣)𝑑𝑣𝑒−𝑎𝑠L 𝑓 𝑡 ∎

7. T r a n s l a s i p a d a s u m b u - t
Contoh
Tentukan L {cos 𝑡 𝑢 (𝑡 − 𝜋)}
Penyelesaian : dengan 𝑔(𝑡) = 𝑐𝑜𝑠 𝑡 dan 𝑎 = 𝜋, maka 𝑔(𝑡 +
𝜋) = 𝑐𝑜𝑠 (𝑡 + 𝜋) = −𝑐𝑜𝑠 𝑡
dengan menggunakan rumus penjumlahan untuk fungsi cos.
(bentuk alternatif teorema translasi kedua)
L {cos 𝑡 𝑢(𝑡 − 𝜋)} = −𝑒−𝑎𝑠 L cos 𝑡 = −
𝑠
𝑠2+1
𝑒−𝜋𝑠 ∎

8. Invers teorema Translasi pertama
Jika L 𝑒 𝑎𝑡
𝑓 𝑡 = 𝐹 𝑠 − 𝑎 maka, L -1{𝐹(𝑠 − 𝑎)} = 𝑒 𝑎𝑡
L -1 𝐹 𝑠 = 𝑒 𝑎𝑡
𝑓(𝑡)
Contoh
Tentukan invers dari transformasi laplace :
1
𝑠−𝑎 2
Penyelasaian
𝐹 𝑠 − 𝑎 =
1
𝑠 − 𝑎 2
, 𝐹 𝑠 =
1
𝑠2
Sehingga , L -1{𝐹(𝑠 − 𝑎)} = 𝑒 𝑎𝑡
L -1 𝐹 𝑠
L -1 1
𝑠−𝑎 2 = 𝑒 𝑎𝑡 L -1 1
𝑠2
L -1 1
𝑠−𝑎 2 = 𝑒 𝑎𝑡 𝑡

9. Invers teorema Translasi kedua
Jika 𝑓 𝑡 = L 𝐹 𝑠 , 𝑎 > 0 maka L -1 𝑒−𝑎𝑠
𝐹 𝑠 = 𝑓 𝑡 − 𝑎 𝑢 𝑡 − 𝑎
Contoh
Tentukan : (𝑎) L -1 1
𝑠−4
𝑒−2𝑠
(𝑏) L -1 𝑠
𝑠2+9
𝑒− 𝜋𝑠
2
Penyelesaian:
(𝑎) dengan mengidentifikasi 𝑎 = 2, 𝐹 𝑠 =
1
(𝑠−4)
dan L -1 𝐹 𝑠 = 𝑒4𝑡
maka L -1 1
𝑠−4
𝑒−2𝑠
= 𝑒4 𝑡−2
𝑢(𝑡 − 2)
(b) dengan 𝑎 =
𝜋
2
𝐹 𝑠 =
2
(𝑠2+9)
dan L -1 𝐹 𝑠 = cos 3𝑡 maka
L -1 𝑠
𝑠2+9
𝑒− 𝜋𝑠
2 = cos 3 𝑡 −
𝜋
2
𝑢 𝑡 −
𝜋
2
Pernyataan terakhir dapat di sederhanakan dengan menggunakan rumus
penjumlahan cos.
Diperoleh hasil yang sama dengan –𝑠𝑖𝑛3𝑡 𝑢 𝑡 −
𝜋
2
∎