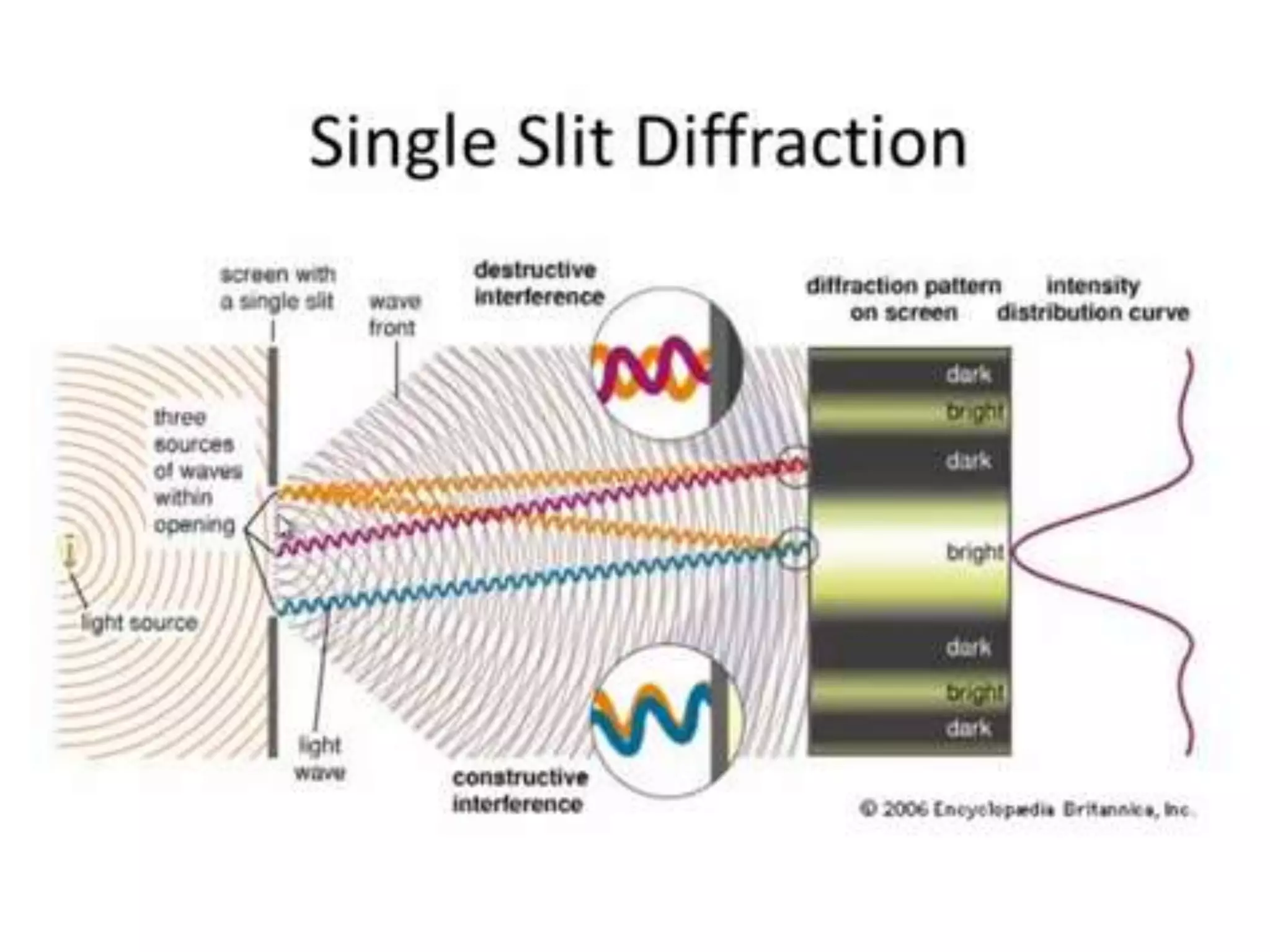
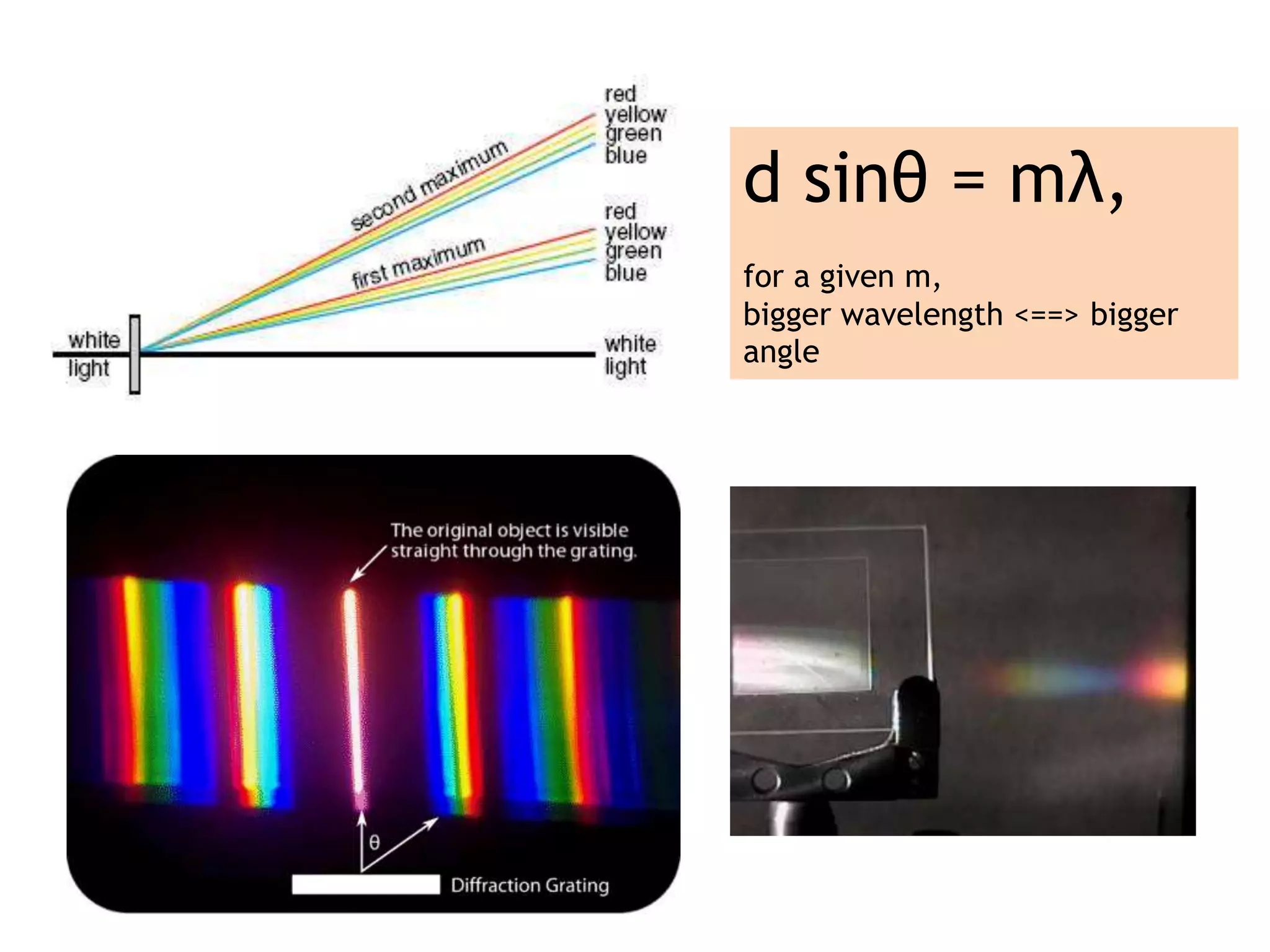
This document discusses various topics in wave optics including wavefronts, interference, diffraction from single and double slits, and diffraction gratings. It defines key terms such as coherence, optical path difference, and constructive and destructive interference. It presents Huygens' principle which describes how wavefronts propagate. Young's double slit experiment is used to demonstrate interference patterns. Formulas are provided for interference fringe spacing, single slit diffraction, and diffraction from diffraction gratings.

1. Topic 4 Wave Optics
• Wave front
• Interference
• Diffraction
- Single slit
- Diffraction grating
• Laser and their uses

2. Wave
A
B
C
D
E
F
G
H
I
J
K
L
M
State the distances that correspond to one .

3. Huygen’s assumption (herhens)
• Light travels in the form of
waves.
• When a point source emit light,
spherical waves propagate from
this source.
• Each sphere is the locus of
points of the same phase.
• Every surface of the sphere is
called a wavefront.
• An arrow represents a ray. The
direction of propagation of the
wave is perpendicular to the
wavefront.

4. Huygen principle on how the wavefronts move
Every point on the wavefront acts as a secondary
point source that is spherical.
After a time t, the position for the next wavefront is
the surface that touches all the wavelets from their
sources.

5. Concept of coherens
• Two wave sources are said to be coherent
sources if both waves have the same
frequency and a constant phase difference.
• This means that both waves have the same
wavelength. When the phase difference is zero, both
waves are said to be in phase.

6. Beza fasa yang tetap

7. Explain if the sources below are
coherent or not.
A B
C D
E

8. Optical path difference
• The difference in distance travelled by two
waves is call the path difference.
Path difference = 

9. What is the path difference in each
situation below?

10. Superposition principle
In phase
Out of
phase
Wave 1
Wave 2
Superposition

11. Interferens
Interferens is the superposition or the addition of
two or more waves.
During interference, the superposition of the waves
can result in a wave of higher amplitude
(constructive interference) or a wave with a smaller
amplitude (destructive interference) depending on
their relative phases.
To get a steady interference pattern
• The two sources must be coherent.
• The two sources are close to each other

12. Constructive interference
When the crest of a wave superimpose on the crest
of another wave, the resultant wave has a higher
amplitude and constructive interference occur.
The place where constructive interference occur is
called the antinode.
For constructive interference to occur,
Path difference = m where m = 0, 1, 2, 3, 4, ...

13. Destructive interference
When the crest of a wave superimpose on the
trough of another wave, the resultant wave has a
lower amplitude and destructive interference occur.
The place where constructive interference occur is
called the node.
For destructive interference to occur,
Path difference = (m+½) where m = 0, 1, 2, 3, 4, ...

14. Interference pattern
Antinode (bright)
Node (dark)

15. Young’s double slit interference pattern
Apakah akan berlaku kepada corak interferens apabila
a) jarak di antara dua sumber bertambah
b) frekuensi sumber berkurang
c) jarak antara sumber dengan layar berkurang

16. Young’s interference formula
Assume that the source is far
from the screen and the sources
are coherent.
Assume screen is far,
therefore  small.
.. 1
For D size of slit,
the blue triangle is
almost a right angle
triangle.
’  
sin ’ = /a ..2
From 1 and 2,
/a = y/D
= ay/D
 = path difference
Adakah interference membina
atau membinasa berlaku
kalau beza lintasan adalah
a) 0
b) ½ 
1
2
3

17. Constructive interference
ay/D = m where m = 0, 1, 2, 3, 4, ...
Destructive interference
ay/D = (m+½) where m = 0, 1, 2, 3, 4, ...

18. Constructive interference
ay/D = m di mana m = 0, 1, 2, 3, 4, ...
When m = 1 ,
Distance between bright fringes, y1 = D/a
y1
m=0
m=1
m=2

19. Single slit diffraction

21. First minima of
single slit
diffraction
sin  = /a ---- 1




22. tan  = y/L -----2
From 1
sin  = /a ---- 1
 small, therefore
 sin   tan 


23. Diffraction grating
When we have more slits like
100 slits per mm,
1. what happens to the bright
lines seen in the single slit
envelope?
2. will we get more bright lines
within the principal maxima of
the single slit?

25. y1 = D/d
y2 = 2D/d
Diffraction grating
d sinθ = mλ
y =L
a
Single slit
Centre of
principal
maxima to first
minima
Double slit
D
e.g. 10000 lines per cm
d = 1x10-6 m
e.g. a = 4x10-6 m
e.g. d = 1.2x10-4 m

26. d sinθ = mλ,
for a given m,
bigger wavelength <==> bigger
angle