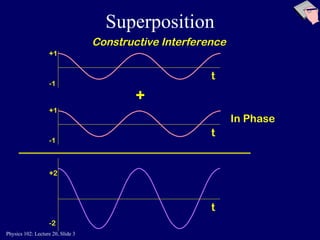
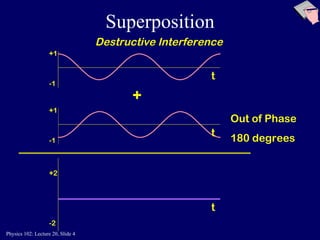
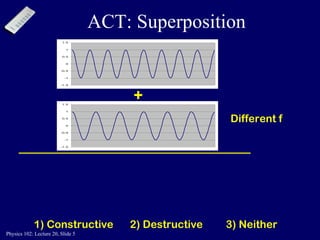
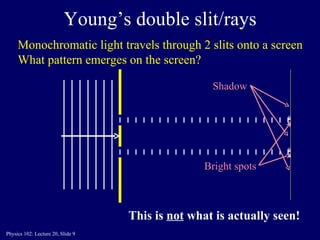
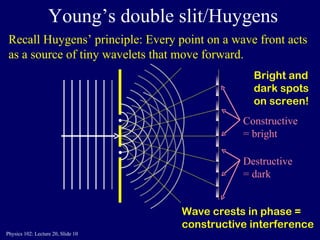
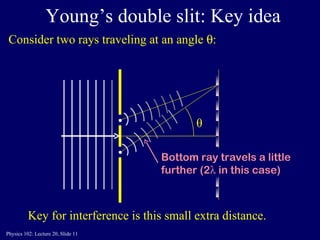
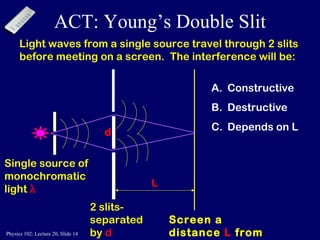
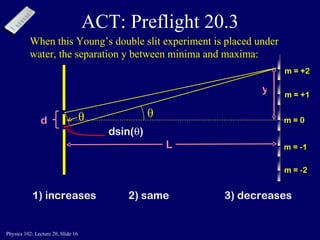
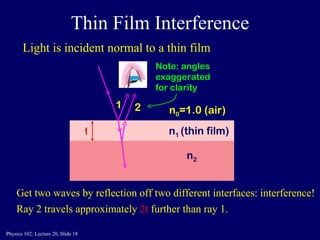
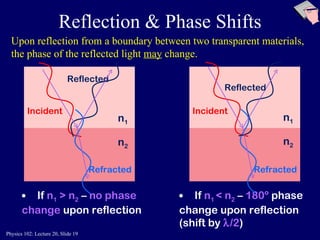
This document discusses the physics concepts of interference and diffraction of light waves. It covers Young's double slit experiment and how constructive and destructive interference creates bright and dark bands on the detection screen. Thin film interference is also discussed, where light reflecting off the top and bottom of a thin film can interfere due to a path length difference of half a wavelength or a multiple thereof.

1. Physics 102: Lecture 20 Interference

3. Superposition + Constructive Interference In Phase t +1 -1 t +1 -1 t +2 -2

4. Superposition t +1 -1 t +1 -1 + Destructive Interference Out of Phase 180 degrees t +2 -2

5. ACT: Superposition + Different f 1) Constructive 2) Destructive 3) Neither

7. Demo: Interference for Sound … For example, a pair of speakers, driven in phase, producing a tone of a single f and  : But this won’t work for light--can’t get coherent sources l 1 l 2 hmmm… I’m just far enough away that l 2 - l 1 =  /2, and I hear no sound at all!

9. Young’s double slit/rays This is not what is actually seen! Monochromatic light travels through 2 slits onto a screen What pattern emerges on the screen? Bright spots Shadow

10. Young’s double slit/Huygens Recall Huygens’ principle: Every point on a wave front acts as a source of tiny wavelets that move forward. Wave crests in phase = constructive interference Bright and dark spots on screen! • • Constructive = bright Destructive = dark

11. Young’s double slit: Key idea Key for interference is this small extra distance. Consider two rays traveling at an angle  : θ • • Bottom ray travels a little further (2  in this case)

12. Young’s double slit: Quantitative Constructive : dsin(  ) = m  Destructive : dsin(  ) = (m+1/2)  Consider two rays traveling at an angle  Assume screen is very far away (L>>d): θ ≈ ≈ ≈ L where m = 0,  1,  2 m = + 2 Need  < d Path length difference = dsin(  ) θ

13. Young’s double slit: Quantitative Constructive : dsin(  ) = m  Destructive : dsin(  ) = (m+1/2)  Assume screen is very far away (L>>d), angles  are small: θ L m = 0,  1,  2 sin(  )  tan(  ) = y/L y ≈ m  L/d y ≈ (m+1/2)  L/d dsin(  ) θ m = 0 m = +1 m = -1 m = -2 m = +2 y

16. ACT: Preflight 20.3 1) increases 2) same 3) decreases θ L When this Young’s double slit experiment is placed under water, the separation y between minima and maxima: dsin(  ) θ m = 0 m = +1 m = -1 m = -2 m = +2 y

17. Preflight 20.2 In the Young double slit experiment, is it possible to see interference maxima when the distance between slits is smaller than the wavelength of light? 1) Yes 2) No

18. Thin Film Interference n 1 (thin film) n 2 n 0 =1.0 (air) t Get two waves by reflection off two different interfaces: interference! Ray 2 travels approximately 2t further than ray 1. Light is incident normal to a thin film 1 2 Note: angles exaggerated for clarity

20. Thin Film Summary n 1 (thin film) n 2 n = 1.0 (air) t 1 2 Ray 1:  1 = 0 or ½ Determine  , number of extra wavelengths for each ray. If |  2 –  1 | = ½ , 1 ½, 2 ½ …. (m + ½) destructive If |  2 –  1 | = 0, 1, 2, 3 …. (m) constructive Note: this is wavelength in film! (  film =  o /n 1 ) + 2 t/  film Ray 2:  2 = 0 or ½ + 0 Reflection Distance This is important!

21. ACT: Thin Film Practice n 1 (thin film) n 2 n = 1.0 (air) t 1 2 Blue light (  0 = 500 nm ) incident on a glass ( n 1 = 1.5 ) cover slip ( t = 167 nm ) floating on top of water ( n 2 = 1.3 ). A)  1 = 0 B)  1 = ½ C)  1 = 1 What is  1 , the total phase shift for ray 1

22. Thin Film Practice Is the interference constructive or destructive or neither ? n 1 (thin film) n 2 n = 1.0 (air) t 1 2 Blue light (  0 = 500 nm ) incident on a glass ( n 1 = 1.5 ) cover slip ( t = 167 nm ) floating on top of water ( n 2 = 1.3 ). Example  1 =  2 = Phase shift = |  2 –  1 | =

23. ACT: Thin Film Practice II n 1 (thin film) n 2 n = 1.0 (air) t 1 2 Blue light (  0 = 500 nm ) incident on a glass ( n 1 = 1.5 ) cover slip ( t = 167 nm ) floating on top of plastic ( n 2 = 1.8 ). Example  1 =  2 = Phase shift = |  2 –  1 | = Is the interference : 1) constructive 2) destructive 3) neither?