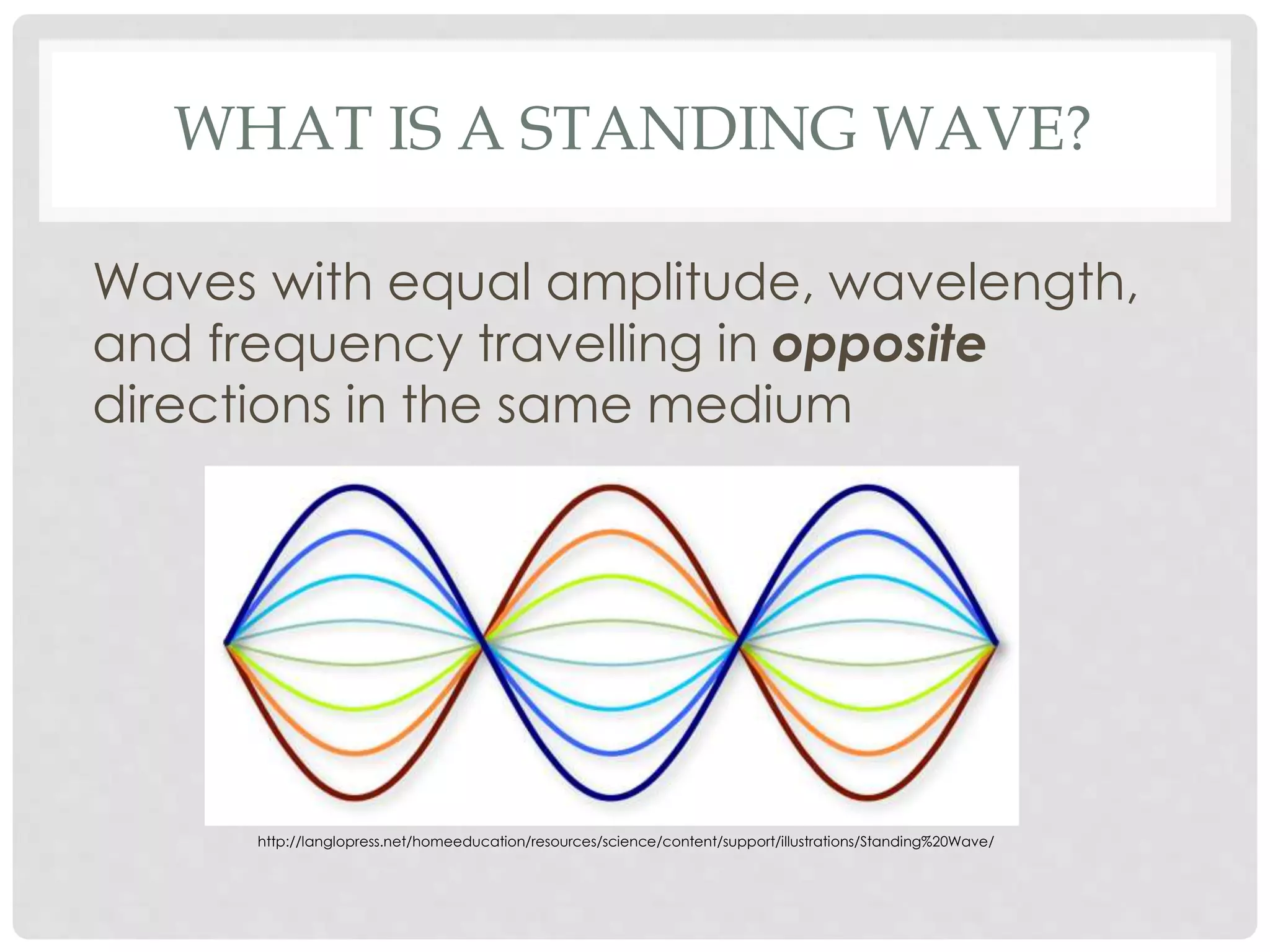
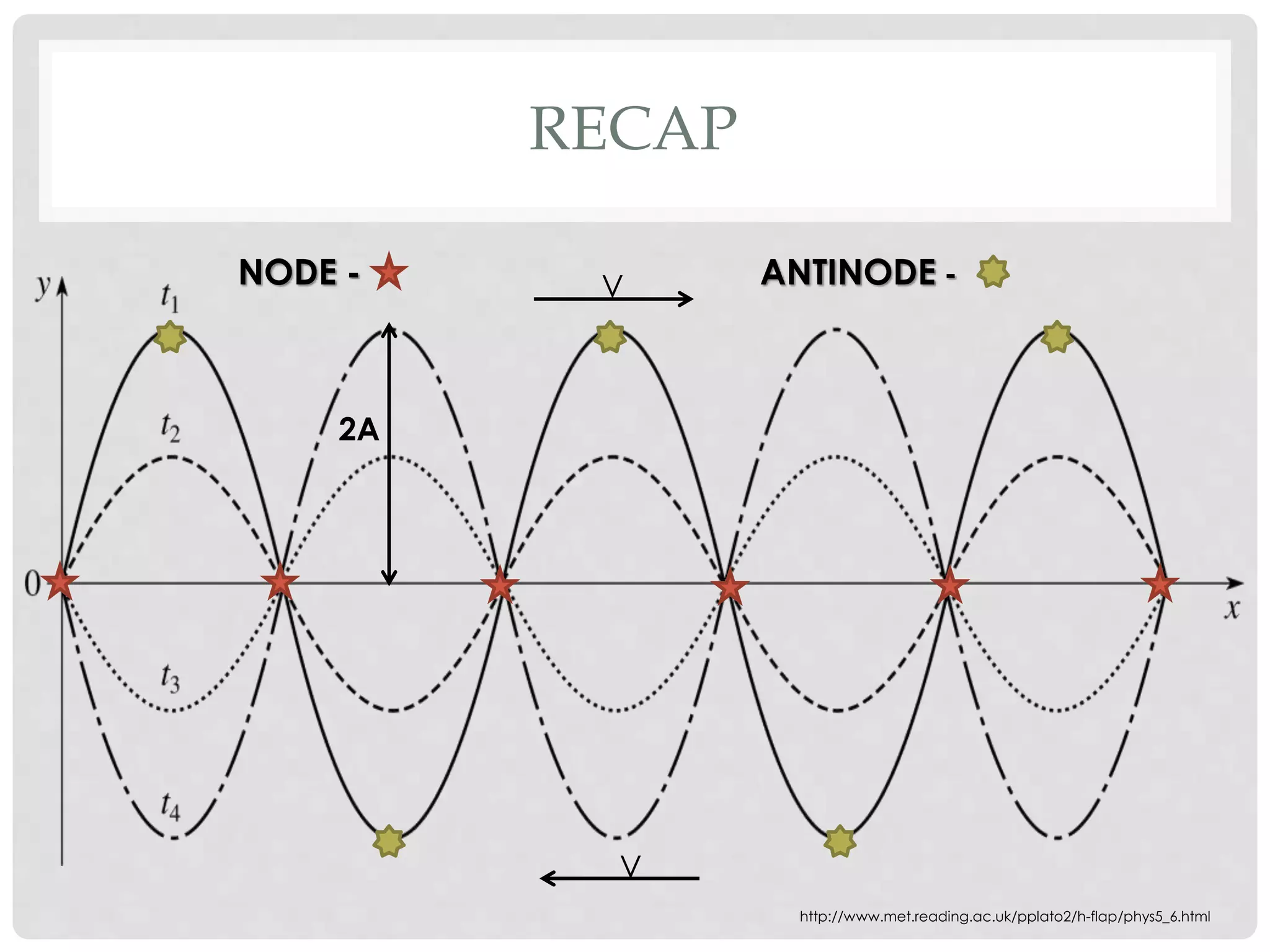
1. A standing wave is formed by two waves of equal amplitude, wavelength, and frequency travelling in opposite directions in the same medium. 2. Nodes occur at positions where the amplitude is zero, while antinodes occur at positions of maximum amplitude. The distance between nodes is half the wavelength, and between a node and adjacent antinode is a quarter wavelength. 3. For a string fixed at both ends, standing waves can form with wavelengths of 2L/m, where L is the string length and m is a positive integer. The lowest frequency is called the fundamental frequency. Higher integer multiples of this frequency are the harmonics.

1. L E A R N I N G O B J E C T V I
J E N N Y H E
STANDING WAVES

2. WHAT IS A STANDING WAVE?
Waves with equal amplitude, wavelength,
and frequency travelling in opposite
directions in the same medium
http://langlopress.net/homeeducation/resources/science/content/support/illustrations/Standing%20Wave/

3. Wave moving right Wave moving left
D1 = Asin(kx-wt) D2 = Asin(kw+wt)
SUPERPOSITION (D1 + D2)
STANDING WAVE
*D(x,t) = 2Asin(kx)cos(wt)
D(x,t) = 2Asin(
2𝜋
𝜆
𝑥)cos(2πft)
***By the Principle of superposition, the resultant wave is the sum of the
individual waves: D1 + D2
EQUATION
*Simplified using Trig. Identity:
sin(a-b)+sin(a+b)=2sin(a)cos(b)

4. EQUATION APPLICATION
• According to the standing wave equation, there is a
position dependent amplitude:
A(x) = 2Asin(kx) = 2Asin(
2𝜋
𝜆
𝑥)
• So, we can simplify the standing wave equation to:
D(x,t) = A(x)cos(wt)
• When D(x,t) = 0 , there is zero amplitude and therefore
exists a NODE
• Similarly, when D(x,t) = 2A, this denotes maximum
amplitude and therefore exists an ANTINODE

5. WHERE ARE THEY LOCATED?
NODES
Occur at A(X)= 2Asin(
𝟐𝝅
𝝀
𝒙)= 0
Solving for x, we get
2𝜋
𝜆
x = 𝜋m, where m=0, ±1, ±2…
Simplify to get: x=m
𝜆
2
,
m=0, ±1, ±2…
So, nodes are found at
x= 0, ±
𝝀
𝟐
, ± 𝝀, ±
𝟑𝝀
𝟐
…
ANTINODES
Occur at A(X)= 2Asin(
𝟐𝝅
𝝀
𝐱)=2A
 Solving for x, we get
2𝜋
𝜆
x = (m+
1
2
)𝜋, m=0, ±1, ±2…
Simplify to get: x=(m+
1
2
)
𝝀
𝟐
m=0, ±1, ±2…
So, antinodes are found at
X= ±
𝝀
𝟒
, ±
𝟑𝝀
𝟒
, ±
𝟓𝝀
𝟒
…

6. RECAP
NODE - ANTINODE -
2A
V
V
http://www.met.reading.ac.uk/pplato2/h-flap/phys5_6.html

7. STANDING WAVES ON STRINGS
• When a string is attached to two fixed ends, waves will
reflect from the fixed ends and travel in opposite
directions: STANDING WAVE!
• If one end is denoted as the origin and the other end is
denoted x=L, the amplitude at the origin and at x=L is 0.
sin(
𝟐𝝅
𝝀
𝒙)= 0 substitute x=L
𝟐𝝅
𝝀
𝐋 = 𝐦 𝝅 m = 1, 2, 3, 4
A string with fixed ends will oscillate with wavelength:
𝝀 =
𝟐𝑳
𝒎
m = 1, 2, 3, 4

8. FUNDAMENTAL FREQUENCY
• Frequency is related to velocity and wave length
by: f=
𝒗
𝝀
; substitute in λ =
2L
m
f=
𝒎𝒗
𝟐𝑳
; V is related to tension and mass density by: √(
𝑻
𝝁
)
So, f=
𝒎
𝟐𝑳
√(
𝑻
𝝁
)
• When the longest wavelength (2L) and lowest frequency
are achieved, it is defined as the fundamental frequency
(first harmonic)
f =
𝟏
𝟐𝑳
√(
𝑻
𝝁
)

9. HARMONICS
• These standing waves are referred
as normal modes of vibration of a
string
• Higher frequencies are often
multiples of fundamental
frequency: fm = mf1 m=1, 2, 3,4…
• These frequencies are known as
harmonics or resonant
frequencies
Fundamental harmonic: f1
Second harmonic: 2f1
Third harmonic: 3f1
Fourth harmonic: 4f1
𝝀 1= 2L
𝝀2= L
𝝀3 =
𝟐𝑳
𝟑
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/string.html

10. PRACTICE PROBLEMS
Q1:
A 65.0 cm long, 7.0 g string
harp string is strummed by
a harpist. It oscillates in its
m=4 mode of vibration with
a frequency of 200 Hz and
an amplitude of 5 cm.
Determine a) wavelength
of the wave and b) tension
in the string.
http://galleryhip.com/harpist-clipart.html

11. SOLUTION TO Q1
• First of all, we know that the
mode is m=4. Which equation will
allow us to determine the
wavelength?
 𝝀 =
𝟐𝑳
𝒎
 𝝀 =
𝟐𝑳
𝟒
=
𝐿
2
• We are given that the length of
string is 65.0 cm
 So 𝝀 =
𝐿
2
=
65.0𝑐𝑚
2
= 32.5 cm =
0.325 m
• Now we are asked to determine
the tension of the string. Which
equations will be useful to use?
 1. V= √(
𝑻
𝝁
) and 2. v= 𝝀f
• By rearranging the 1st equation,
we get T= V2 𝝁. Do we know
what v and 𝜇 are?
• Since we are given the mass
and length of string, we can
first determine 𝜇
• 𝜇 =
𝑚
𝐿
=
0.007 𝑘𝑔
0.65 𝑚
= 0.0108 kg/m
• Now we are only missing V.
What other information are we
given? We are given the
frequency, and we calculated
the wavelength in a. Therefore,
we can use v= 𝝀f relationship

12. SOLUTION TO Q1 (CONT.)
• v= 𝝀f = (0.325 m) (200 Hz) = 65.0 m/s
• Now we have all the required information to solve
for T= V2 𝝁
T = (65.0 m/s) 2 (0.0108 kg/m)
T = 45.6 N

13. PRACTICE PROBLEMS
Q2: A ukelele string oscillates in a standing wave pattern
by :
D(x,t) = 2.0 cm (sin(0.5x))(cos(10π)t)
X= meters t=seconds
a) What is the wavelength and frequency of the standing
wave?
b) Determine the distance between two consectuive
nodes and between a node and an adjacent
antinode.
c) What is the displacement for a particle located at
x=0.1m when t=3 s?

14. SOLUTION TO Q2
a) To determine the wavelength,
we can use the relationship: k=
2𝜋
𝝀
From the given equation, we
know k=0.5 rad/m
So, 𝝀=
2𝜋
0.5
= 4πm
Next, we know the value of w
from the equation, so we can use
w= 2 𝜋 f to solve for frequency.
f=
𝑤
2𝜋
=
10𝜋
2𝜋
= 5.0 Hz
b) The distance between two
consecutive nodes is half a
wavelength. Knowing this, we
can divide the wavelength
calculated in part a by two
4𝜋
2
= 2π m
The distance between two
consecutive antinodes is quarter
of a wavelength. Therefore, we
can multiply ¼ to 4 𝜋 and we get
𝜋 m.

15. SOLUTION TO Q2 (CONT.)
c) The given equations is:
D(x,t) = 2.0 cm (sin(0.5x))(cos(10π)t)
To evaluate the displacement at x=0.1m and t=3.0 s,
we simply plug in the values into the given equation.
D(0.1m, 3.0s) = 0.02 m[sin(0.5(0.1m))][cos(10π(3s))]
= 0.00099958…
= 0.001 m or 1 mm