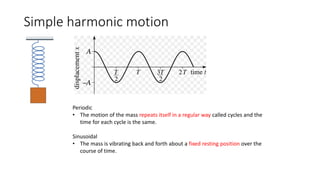
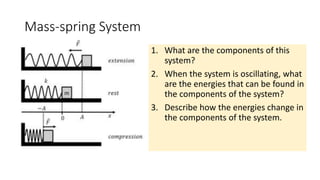
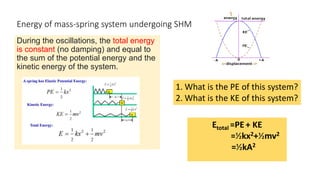
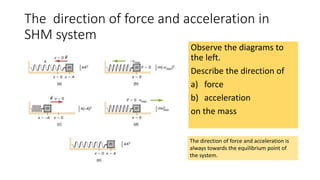
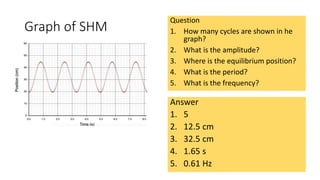
1) Simple harmonic motion (SHM) is the periodic motion of an object where its acceleration is always towards the equilibrium position and is proportional to the distance from that position. 2) SHM is characterized by sinusoidal motion with a fixed amplitude, period, and frequency. The motion repeats in cycles of equal time periods. 3) A mass undergoing SHM has maximum velocity when passing through the equilibrium position and zero velocity at the extreme positions, with velocity changing direction at the equilibrium position.

1. Topic 1a
Simple Harmonic Motion
Cycle, amplitude, period, frequency
Energy
Equations

2. Simple harmonic motion
Periodic
• The motion of the mass repeats itself in a regular way called cycles and the
time for each cycle is the same.
Sinusoidal
• The mass is vibrating back and forth about a fixed resting position over the
course of time.

3. Sinusoidal motion
One complete cycle
Amplitude
Period
Frequency
1. How many cycles are shown in
the graph?
2. What is the amplitude?
3. What is the period?
4. What is the frequency?
1. 2 ¼
2. A
3. T
4. 1/T

4. Graph of SHM
Question
1. How many cycles are shown in he
graph?
2. What is the amplitude?
3. Where is the equilibrium position?
4. What is the period?
5. What is the frequency?
Answer
1. 5
2. 12.5 cm
3. 32.5 cm
4. 1.65 s
5. 0.61 Hz

5. Motion in SHM systems
1. Is the velocity of the mass the same
throughout the motion?
2. What is the velocity of the mass at
point A?
3. What is the velocity of the mass at
point B?
4. What is the velocity of the mass at
point C?
5. Describe what happens in terms of
the mass’ velocity when the mass
moves from
a) A to B
b) B to C
c) C to B
d) B to A
A
B
C
Answers: 1. No , 2. 0, 3. Max, 4. 0, 5a) speeds
up, downwards 5b) slows down, downwards 5c)
speeds up, upward 5d) slows down, upwards

6. Which of the two graphs,
a) or b) is the velocity-time
graph for the position-time
graph above?
a)
b)
a

7. Mass-spring System
1. What are the components of this
system?
2. When the system is oscillating, what
are the energies that can be found in
the components of the system?
3. Describe how the energies change in
the components of the system.

8. Energy of mass-spring system undergoing SHM
During the oscillations, the total energy
is constant (no damping) and equal to
the sum of the potential energy and the
kinetic energy of the system.
Etotal =PE + KE
=½kx2+½mv2
=½kA2
1. What is the PE of this system?
2. What is the KE of this system?

9. Energy of pendulum undergoing SHM
Etotal =PE+ KE
=mgh+½mv2
1. What is the formula for the potential
energy of the system?
2. What is the formula for the kinetic
energy of the system?
In a SHM kinetic and potential energies becomes equal
when the displacement is 1/√(2) times the amplitude.

10. The direction of force and acceleration in
SHM system
Observe the diagrams to
the left.
Describe the direction of
a) force
b) acceleration
on the mass
The direction of force and acceleration is
always towards the equilibrium point of
the system.

11. SHM equations
System starting at
equilibrium
System starting at
maximum
displacement
x = Asin(t)
v = Acos(t)
a = -A2sin(t)
x = Acos(t)
v = -Asin(t)
a = -A2cos(t)
a=-2x
For spring-mass system
=
𝑘
𝑚
T = 2/ = 2 
𝑚
𝑘
For pendulum
=
𝑔
𝑙
T = 2/ = 2 
𝑙
𝑔
=2f
T=1/f

12. Simple harmonic motion (SHM)
Simple harmonic motion is a periodic motion of an
object such that its acceleration is always towards
the equilibrium position and is proportional to its
distance from that position.