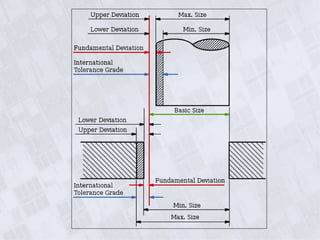
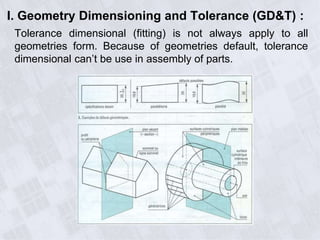
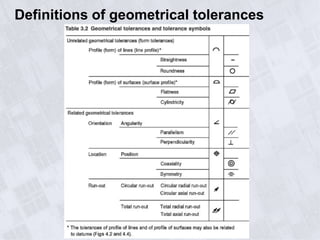
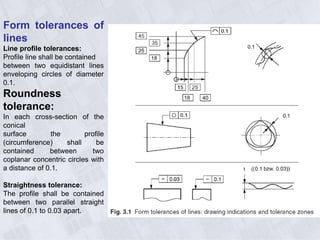
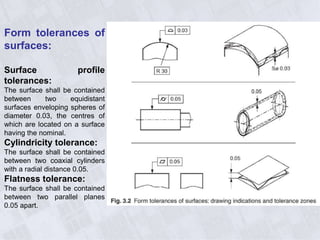
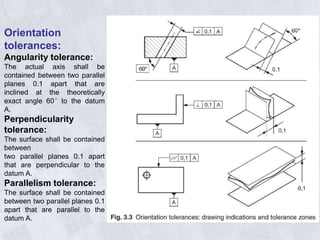
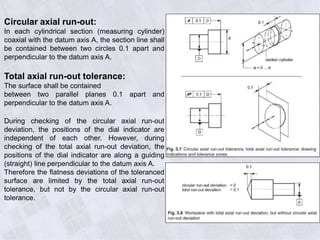
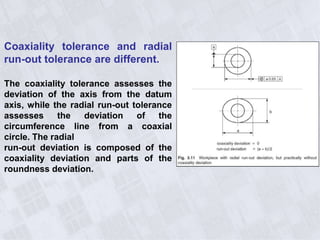
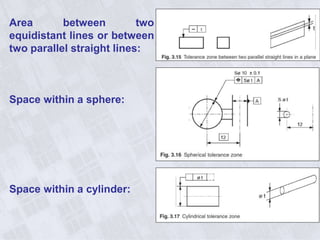
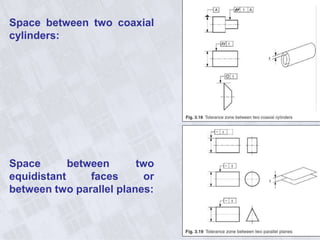
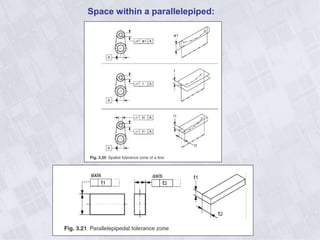
This document provides information on geometry dimensioning and tolerance. It defines dimensional tolerances and discusses their importance in assembly. It then discusses geometric dimensioning and tolerancing (GD&T), including its advantages over traditional tolerancing methods. The document outlines various GD&T symbols and their definitions, including form, orientation, location, runout, and other tolerances. It clarifies the differences between tolerances such as coaxiality and radial runout. Finally, it presents possibilities for geometrically tolerancing different features.

1. Chapter III:
Geometry Dimensioning
Tolerance
គុណភាព​និង សភាព​ននផ្ទៃទលិតទលមេកានិច
Prepared by: Sry Vannei

2.  Review of Interchangeable:
It uses for producing the mechanical production in series.
They are made to specifications that they are so nearly identical
which will fit into any device of the same type. One such part
can freely replace another, without any custom fitting. This
interchangeability allows easy assembly of new devices, and
easier repair of existing devices, while minimizing both the time
and skill required of the person doing the assembly or repair.

3. Dimensional Tolerances:
It is defined as the permissible or acceptable variation
in the dimensions (height, width, depth, diameter,
angles) of a part. The root of the word tolerance is the
Lantin tolerance, meaning to endure or put up with.
Tolerances are unavoidable because it is virtually
impossible to manufacture two parts that have
precisely the same dimensions. Furthermore, because
close dimensional tolerances can significantly increase
the product cost, a narrow tolerance range is
undesirable economically. However, for some parts,
close tolerances are necessary for proper functioning,
and are therefore worth the added expense associated
with narrow tolerance ranges. Examples are precision
measuring instruments and gages, hydraulic pistons,
and bearings for aircraft engines.

5. Fitting:
Dimensional tolerances become important only
when a part is to be assembled or mated with
another part. Surfaces that are free and not
functional do not need close tolerance control.
Importance of Dimensional Tolerance Control:
Dimensional tolerances become important only
when a part is to be assembled or mated with
another part. Surfaces that are free and not
functional do not need close tolerance control.

6. Tolerance dimensional (fitting) is not always apply to all
geometries form. Because of geometries default, tolerance
dimensional can’t be use in assembly of parts.
I. Geometry Dimensioning and Tolerance (GD&T) :

7. What is GD&T ?
GD&T is a symbolic language. It is used to specify
the size, shape, form, orientation, and location of
features on a part. Features toleranced with GD&T
reflect the actual relationship between mating parts.
Drawings with properly applied geometric tolerancing
provide the best opportunity for uniform interpretation
and cost-effective assembly. GD&T was created to
insure the proper assembly of mating parts, to
improve quality, and to reduce cost.

8. When should GD&T be used?
Designers should tolerance parts with GD&T when:
 Drawing delineation and interpretation need to be the
same.
 Features are critical to function or interchangeability.
 It is important to stop scrapping perfectly good parts.
 It is important to reduce drawing changes.
 Automated equipment is used.
 Functional gaging is required.
 It is important to increase productivity.
 Companies want across-the-board savings.

9.  Advantages of GD&T over Coordinate Dimensioning
and Tolerance :
Plus or minus tolerancing system for tolerancing drawings have
several limitation:
 The plus or minus tolerancing system generates rectangular
tolerance zones. Rectangular tolerance zones do not have a
uniform distance from the center to the outer edge.
 Size features can only be specified at the location tolerance
of feature size condition and if the size of the features
change, there is no way to specify location of tolerance.
 Datums are usually not specified where the plus or minus
tolerancing system is used.

10.  Symbol

14. Definitions of geometrical tolerances

15. Form tolerances of
lines
Line profile tolerances:
Profile line shall be contained
between two equidistant lines
enveloping circles of diameter
0.1.
Roundness
tolerance:
In each cross-section of the
conical
surface the profile
(circumference) shall be
contained between two
coplanar concentric circles with
a distance of 0.1.
Straightness tolerance:
The profile shall be contained
between two parallel straight
lines of 0.1 to 0.03 apart.

16. Form tolerances of
surfaces:
Surface profile
tolerances:
The surface shall be contained
between two equidistant
surfaces enveloping spheres of
diameter 0.03, the centres of
which are located on a surface
having the nominal.
Cylindricity tolerance:
The surface shall be contained
between two coaxial cylinders
with a radial distance 0.05.
Flatness tolerance:
The surface shall be contained
between two parallel planes
0.05 apart.

17. Orientation
tolerances:
Angularity tolerance:
The actual axis shall be
contained between two parallel
planes 0.1 apart that are
inclined at the theoretically
exact angle 60°to the datum
A.
Perpendicularity
tolerance:
The surface shall be contained
between
two parallel planes 0.1 apart
that are perpendicular to the
datum A.
Parallelism tolerance:
The surface shall be contained
between two parallel planes 0.1
apart that are parallel to the
datum A.

18. Location tolerances:
Positional tolerances:
The theoretical exact (nominal) position is defined
by the theoretical exact dimensions (TEDs) with
respect to the datums A, B and C. The actual axis
shall be contained within a cylinder of diameter 0.1,
with an axis that coincides
with the theoretical exact position.
Coaxiality tolerance:
The actual axis shall be contained within a cylinder
of diameter 0.03 coaxial with the datum axis A.
When the features are practically two dimensional
(thin sheet, engraving) the tolerance is also
referred to as the concentricity tolerance.
Symmetry tolerance:
The actual median face shall be contained between
two parallel planes 0.08 apart that are
symmetrically disposed about the datum median
plane B.

19. Radial run-out tolerances:
Circular radial run-out:
In each plane perpendicular to the common
datum axis A–B the profile (circumference)
shall be contained between two circles
concentric with the datum axis A–B and with
a radial distance of 0.1.
Total radial run-out tolerance:
The surface shall be contained between two
cylinders coaxial with the datum axis A–B
and with a radial distance of 0.1.
During checking of the circular radial run-
out deviation, the positions of the dial
indicator are independent of each other.
However, during checking of the total radial
run-out deviation, the positions of the dial
indicator are along a guiding (straight) line
parallel to the datum axis A–B.
Therefore the straightness deviations and
the parallelism deviations of the generator
lines of the toleranced cylindrical surface
are limited by the total radial run-out
tolerance, but not by the circular radial run-
out tolerance.

20. Circular axial run-out:
In each cylindrical section (measuring cylinder)
coaxial with the datum axis A, the section line shall
be contained between two circles 0.1 apart and
perpendicular to the datum axis A.
Total axial run-out tolerance:
The surface shall be contained
between two parallel planes 0.1 apart and
perpendicular to the datum axis A.
During checking of the circular axial run-out
deviation, the positions of the dial indicator are
independent of each other. However, during
checking of the total axial run-out deviation, the
positions of the dial indicator are along a guiding
(straight) line perpendicular to the datum axis A.
Therefore the flatness deviations of the toleranced
surface are limited by the total axial run-out
tolerance, but not by the circular axial run-out
tolerance.

21. Run-out tolerances in any
direction:
Circular run-out tolerance in any direction:
In each conical section (measuring cone) coaxial with
the datum axis B and perpendicular to the nominal
toleranced surface (defining the measuring cone
angle) the section line shall be contained between two
circles 0.1 apart and perpendicular to the datum axis
B.
Total run-out tolerance in any direction:
The surface shall be contained between two cones
coaxial with the datum axis B and with a radial
distance of 0.1 (measured perpendicular to the
nominal cone surfaces).
During checking of the circular run-out deviation in
any direction, the positions of the dial indicator are
independent of each other. However, during checking
of the total amount deviation in any direction, the
positions of the dial indicator are along a guiding line
(theoretical exact generator line of the toleranced
future) parallel to its theoretical exact position with
respect to the datum axis B.
Therefore the deviations of the generator line of the
toleranced feature are limited by the total run-out
tolerance in any direction, but not by the circular run-
out tolerance in any direction.

22. Coaxiality tolerance and radial
run-out tolerance are different.
The coaxiality tolerance assesses the
deviation of the axis from the datum
axis, while the radial run-out tolerance
assesses the deviation of the
circumference line from a coaxial
circle. The radial
run-out deviation is composed of the
coaxiality deviation and parts of the
roundness deviation.

23. Possibilities of geometrical tolerancing of
features are listed in Table 3.3:

24. Tolerance Zone:
Form of the tolerance zone:
Depending on the toleranced characteristic and depending on the
drawing indication the tolerance zone is one of the following:
Area within a circle:
Area between two concentric circles:

25. Area between two
equidistant lines or between
two parallel straight lines:
Space within a sphere:
Space within a cylinder:

26. Space between two coaxial
cylinders:
Space between two
equidistant faces or
between two parallel planes:

27. Space within a parallelepiped: