Downloaded 68 times
Uploaded byVelmurugan Sivaraman
Dimensional engineering
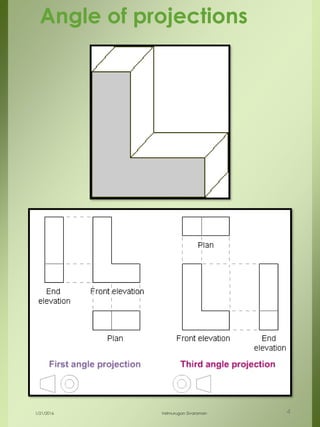
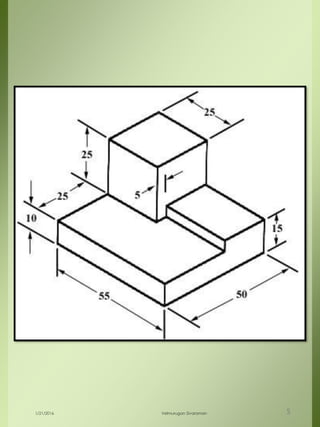
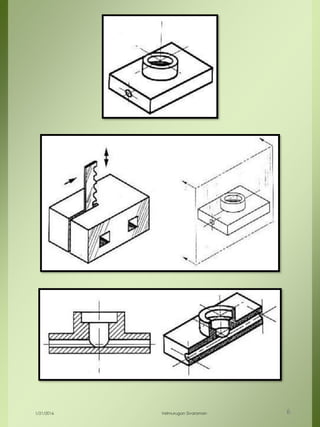
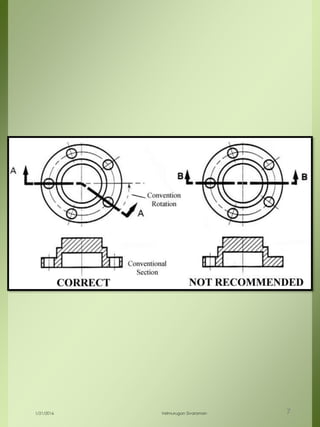
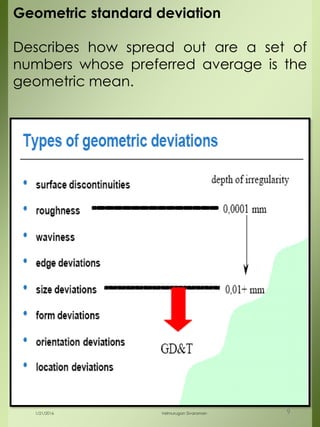
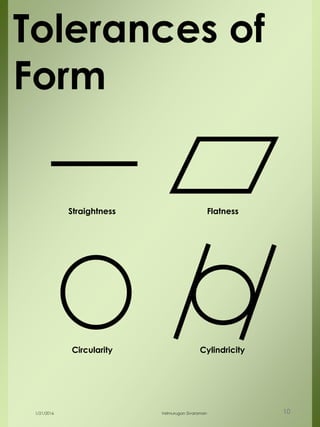
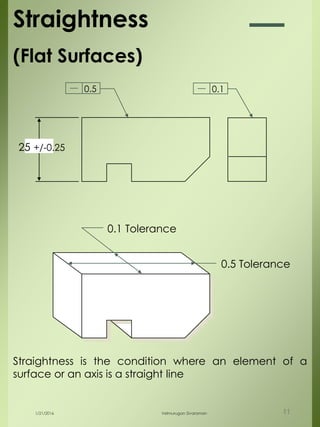
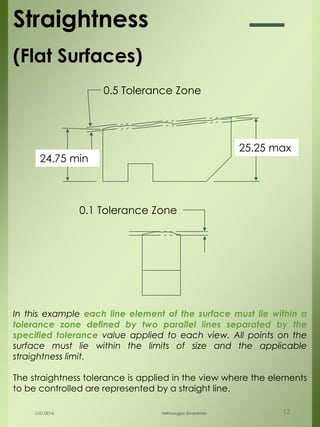
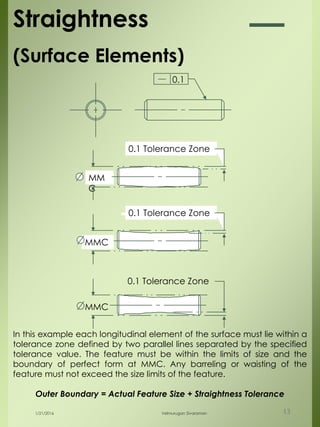
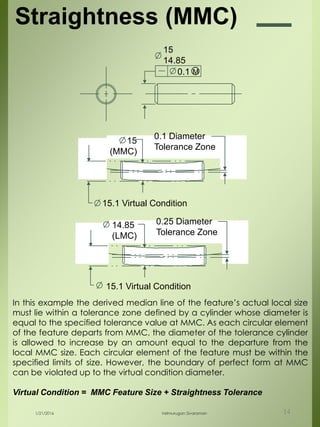
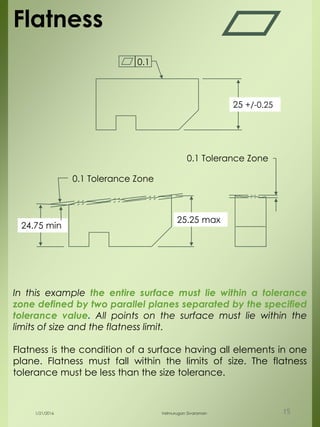
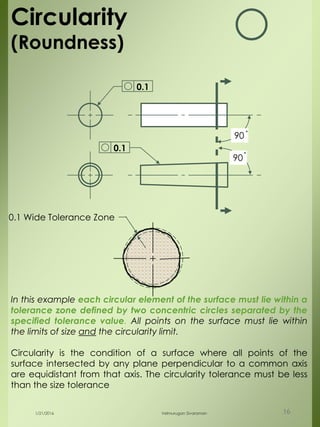
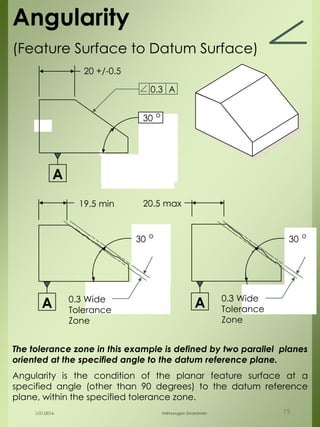
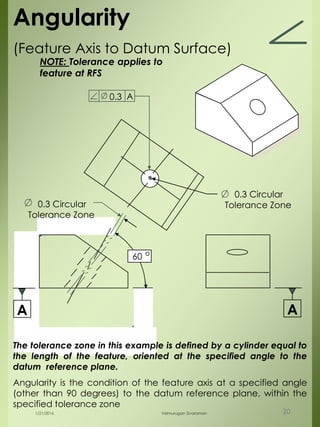
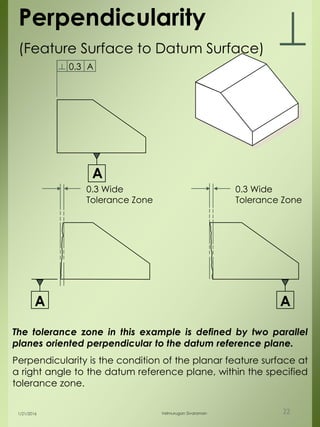
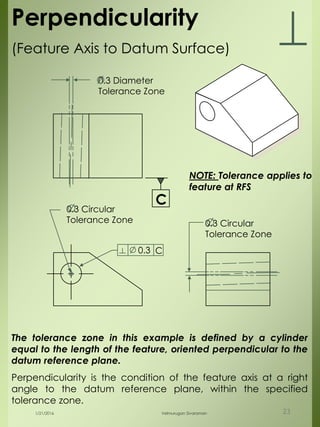
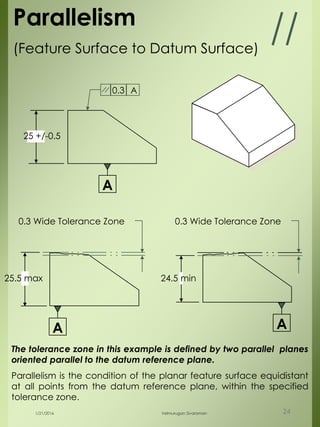
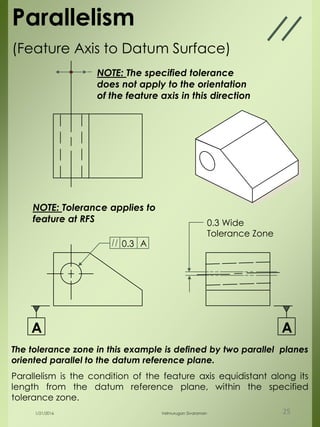
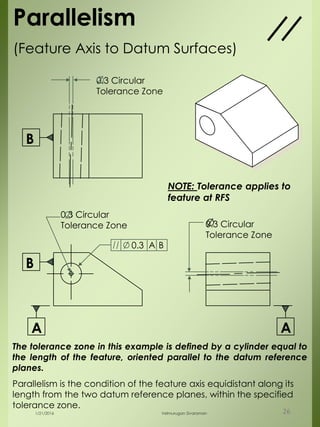
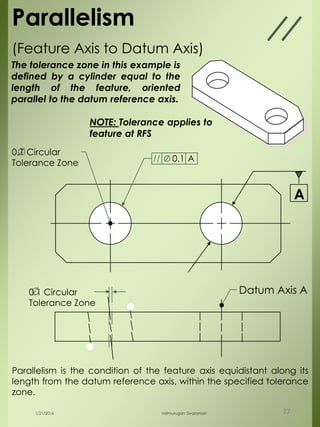
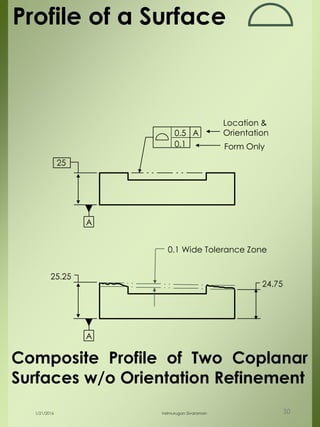
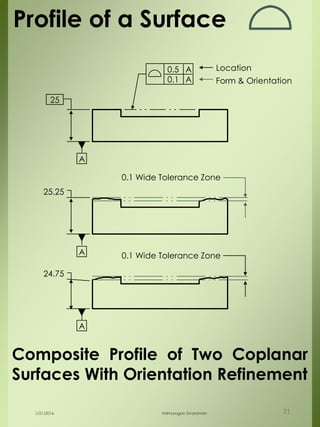
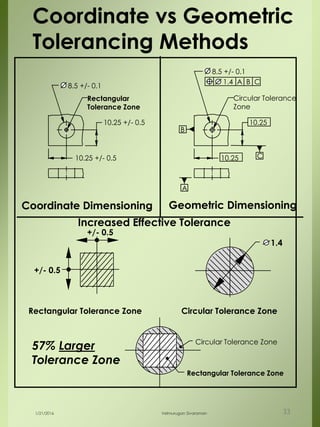
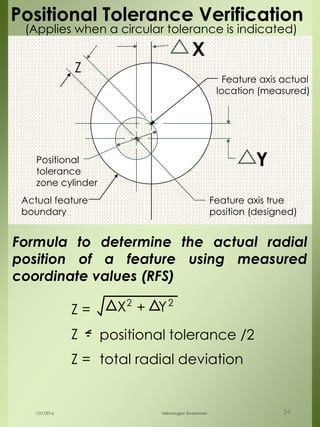
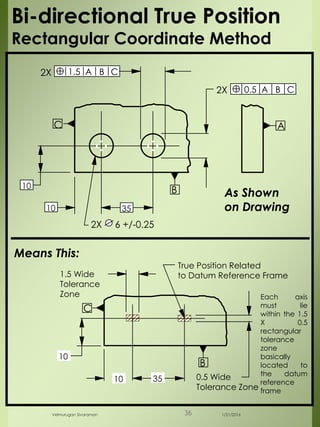
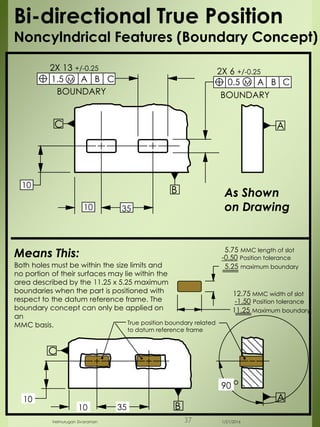
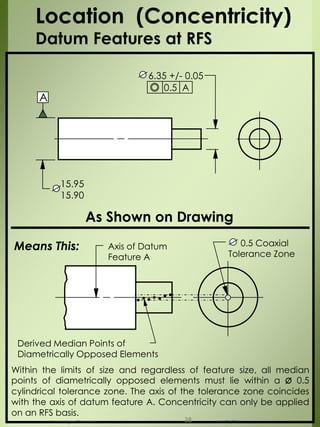
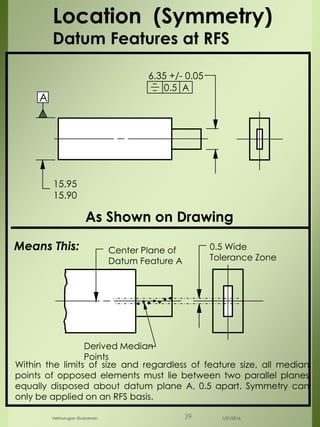
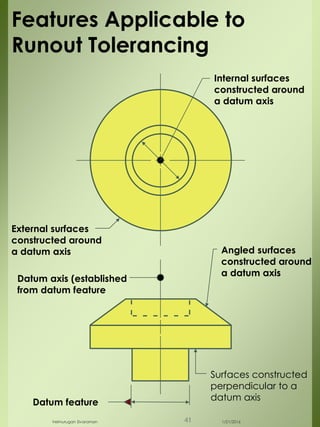
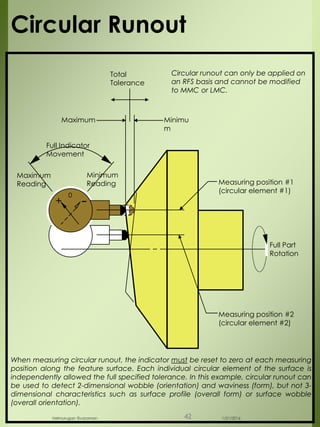
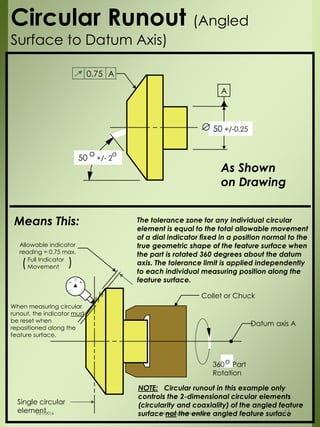
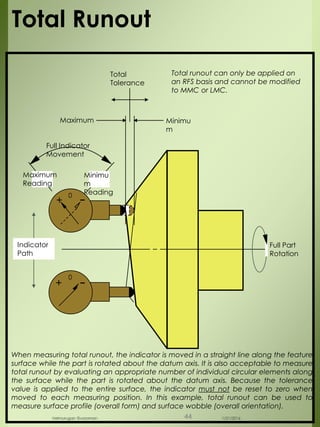
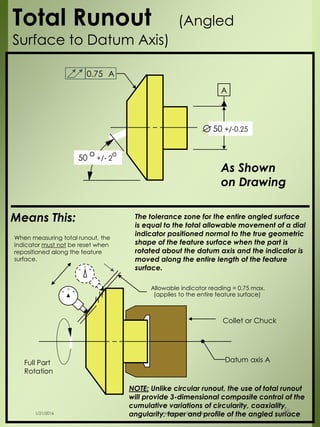
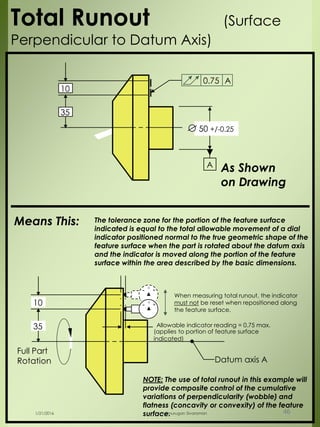
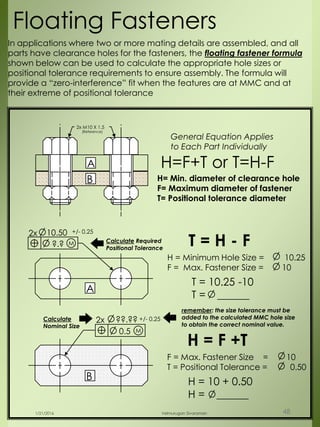
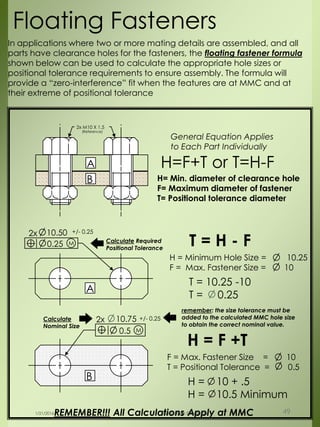
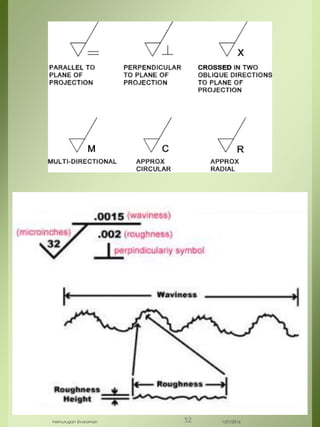
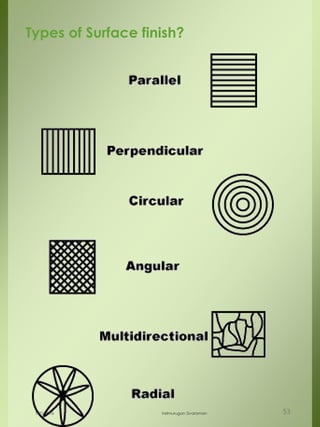
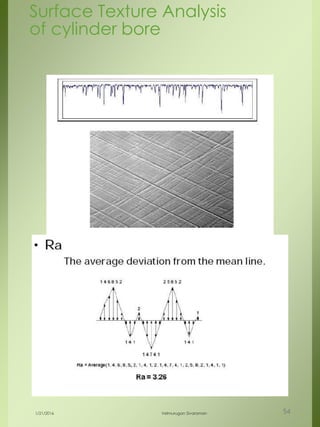
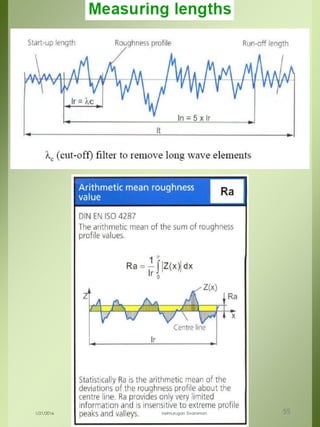
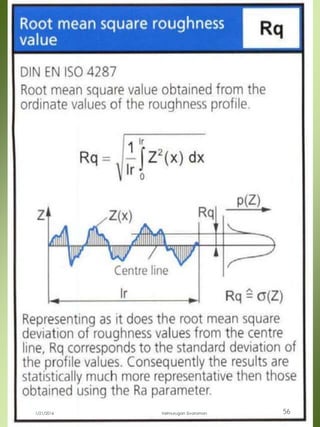
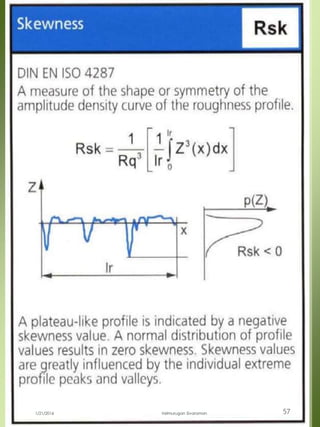
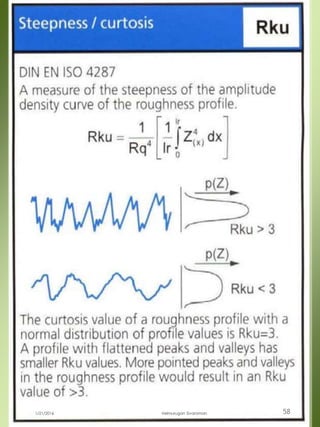
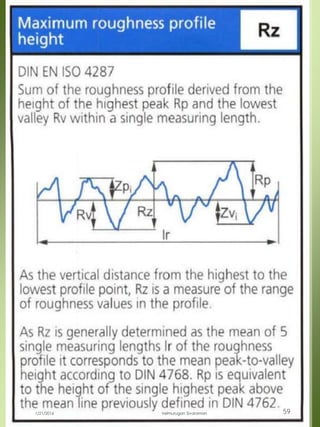
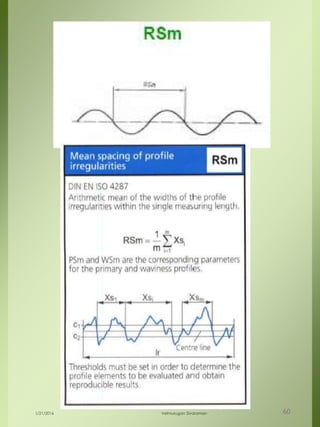
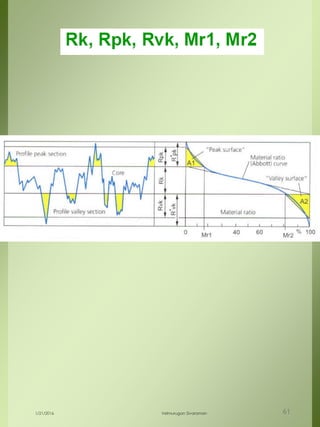
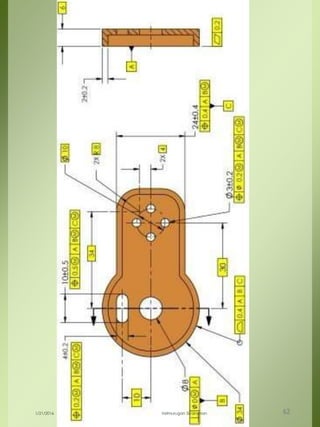
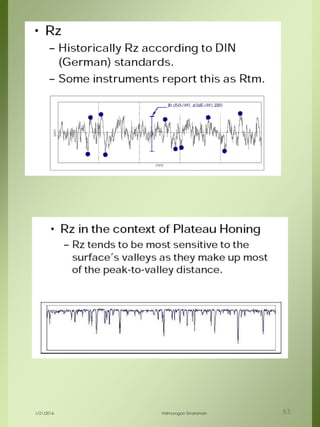
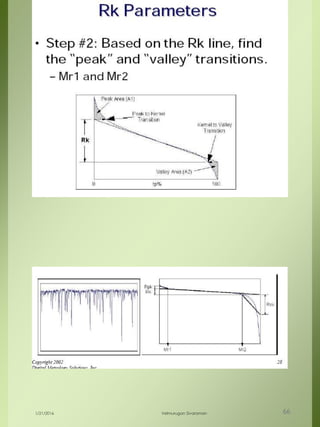
The document provides a comprehensive overview of dimensional engineering, particularly focusing on dimensioning and tolerancing standards. It defines dimensions in various contexts, such as linear and angular measurements, and elaborates on tolerance concepts, including straightness, flatness, circularity, and cylindricity. Additionally, it covers principles of location and runout, explaining tolerance zones and their application in engineering drawings.
In this document
Powered by AI
Introduction to the presentation and focus on ASME Y14.5M-1994 standards for dimensioning.
Dimensions define object characteristics like length, width, height, and include multiple dimensions.
Definition of tolerance in measurements; includes types and applications like straightness and flatness.
Specific tolerances types like flatness, circularity, and cylindricity with specifications and examples.
Focuses on angularity, perpendicularity, and parallelism tolerances with definitions and visual representations.
Introduction to profile tolerances including profile of a line and surface, emphasizing form and orientation.
Details on true position, concentricity, symmetry and their application with diagrams and formulae.
Covers runout tolerances, circular and total runout concepts related to features and measurement techniques.
Details on calculations related to fixed and floating fasteners, ensuring proper assembly and tolerances.
Definition of surface finish, its importance, and types of finish related to machined surfaces.
Final thoughts, including summaries and visuals without specific informative content.
More Related Content
Similar to Dimensional engineering
Dimensional engineering
- 1. DIMENSIONAL ENGINEERING Compiled &Edited Velmurugan Sivaraman Welcome!
- 2. Based on theASME Y14.5M-1994 Dimensioning and Tolerancing Standard DIMENSIONAL ENGINEERING 1/21/2016 Velmurugan Sivaraman 2 Compiled & Edited Velmurugan Sivaraman
- 3. Dimension (Latin, "measuredout") is a parameter or measurement required to define the characteristics of an object - i.e. length, width, and height or size and shape. What is dimension? Types 2nd dimensional For example, locating a point on a plane requires two parameters - latitude and longitude. 3rd dimensional Locating the exact position of an aircraft in flight (relative to the Earth) requires another dimension (altitude) with latitude and longitude. 4th dimension aircraft's estimated "speed" may be calculated from a comparison between the times associated with any two positions. 1/21/2016 Velmurugan Sivaraman 3
- 4. Angle of projections 1/21/2016Velmurugan Sivaraman 4
- 5.
- 6.
- 7.
- 8. What is tolerance? Itis almost impossible to maintain the strict degree of accuracy as listed on a plan. To accommodate this, it is normal to display measurements with a plus or minus (+/-) tolerance which allows for some margin of error. 1/21/2016 Velmurugan Sivaraman 8 What is tolerance?
- 9. Geometric standard deviation Describeshow spread out are a set of numbers whose preferred average is the geometric mean. 1/21/2016 Velmurugan Sivaraman 9
- 10. Tolerances of Form Straightness Flatness CircularityCylindricity 1/21/2016 Velmurugan Sivaraman 10
- 11. 25 +/-0.25 0.1 Tolerance 0.5Tolerance Straightness is the condition where an element of a surface or an axis is a straight line Straightness (Flat Surfaces) 0.5 0.1 1/21/2016 Velmurugan Sivaraman 11
- 12. 24.75 min 25.25 max 0.5Tolerance Zone 0.1 Tolerance Zone In this example each line element of the surface must lie within a tolerance zone defined by two parallel lines separated by the specified tolerance value applied to each view. All points on the surface must lie within the limits of size and the applicable straightness limit. The straightness tolerance is applied in the view where the elements to be controlled are represented by a straight line. 1/21/2016 Velmurugan Sivaraman 12 Straightness (Flat Surfaces)
- 13. Straightness (Surface Elements) MMC 0.1 ToleranceZone 0.1 MM C 0.1 Tolerance Zone MMC 0.1 Tolerance Zone In this example each longitudinal element of the surface must lie within a tolerance zone defined by two parallel lines separated by the specified tolerance value. The feature must be within the limits of size and the boundary of perfect form at MMC. Any barreling or waisting of the feature must not exceed the size limits of the feature. Outer Boundary = Actual Feature Size + Straightness Tolerance 1/21/2016 Velmurugan Sivaraman 13
- 14. Straightness (MMC) 15 14.85 15.1 VirtualCondition 15 (MMC) 0.1 Diameter Tolerance Zone 15.1 Virtual Condition 14.85 (LMC) 0.25 Diameter Tolerance Zone In this example the derived median line of the feature’s actual local size must lie within a tolerance zone defined by a cylinder whose diameter is equal to the specified tolerance value at MMC. As each circular element of the feature departs from MMC, the diameter of the tolerance cylinder is allowed to increase by an amount equal to the departure from the local MMC size. Each circular element of the feature must be within the specified limits of size. However, the boundary of perfect form at MMC can be violated up to the virtual condition diameter. Virtual Condition = MMC Feature Size + Straightness Tolerance 0.1 M 1/21/2016 Velmurugan Sivaraman 14
- 15. Flatness 25 +/-0.25 24.75 min 25.25max 0.1 0.1 Tolerance Zone 0.1 Tolerance Zone In this example the entire surface must lie within a tolerance zone defined by two parallel planes separated by the specified tolerance value. All points on the surface must lie within the limits of size and the flatness limit. Flatness is the condition of a surface having all elements in one plane. Flatness must fall within the limits of size. The flatness tolerance must be less than the size tolerance. 1/21/2016 Velmurugan Sivaraman 15
- 16. 90 90 0.1 0.1 Wide ToleranceZone Circularity (Roundness) In this example each circular element of the surface must lie within a tolerance zone defined by two concentric circles separated by the specified tolerance value. All points on the surface must lie within the limits of size and the circularity limit. Circularity is the condition of a surface where all points of the surface intersected by any plane perpendicular to a common axis are equidistant from that axis. The circularity tolerance must be less than the size tolerance 0.1 1/21/2016 Velmurugan Sivaraman 16
- 17. Cylindricity 0.1 Tolerance Zone MMC 0.1 Inthis example the entire surface must lie within a tolerance zone defined by two concentric cylinders separated by the specified tolerance value. All points on the surface must lie within the limits of size and the cylindricity limit. Cylindricity is the condition of a surface of revolution in which all points are equidistant from a common axis. Cylindricity is a composite control of form which includes circularity (roundness), straightness, and taper of a cylindrical feature. 1/21/2016 Velmurugan Sivaraman 17
- 18.
- 19. Angularity (Feature Surface toDatum Surface) A 20 +/-0.5 30 o A 19.5 min 0.3 Wide Tolerance Zone 30 o A 20.5 max 0.3 Wide Tolerance Zone 30 o The tolerance zone in this example is defined by two parallel planes oriented at the specified angle to the datum reference plane. Angularity is the condition of the planar feature surface at a specified angle (other than 90 degrees) to the datum reference plane, within the specified tolerance zone. 0.3 A 1/21/2016 Velmurugan Sivaraman 19
- 20. A 0.3 A A 60 o Thetolerance zone in this example is defined by a cylinder equal to the length of the feature, oriented at the specified angle to the datum reference plane. Angularity is the condition of the feature axis at a specified angle (other than 90 degrees) to the datum reference plane, within the specified tolerance zone 0.3 Circular Tolerance Zone 0.3 Circular Tolerance Zone Angularity (Feature Axis to Datum Surface) NOTE: Tolerance applies to feature at RFS 1/21/2016 Velmurugan Sivaraman 20
- 21. 0.3 Circular Tolerance Zone NOTE:Tolerance applies to feature at RFS 0.3 Circular Tolerance Zone A Datum Axis A Angularity (Feature Axis to Datum Axis) The tolerance zone in this example is defined by a cylinder equal to the length of the feature, oriented at the specified angle to the datum reference axis. Angularity is the condition of the feature axis at a specified angle (other than 90 degrees) to the datum reference axis, within the specified tolerance zone. NOTE: Feature axis must lie within tolerance zone cylinder 0.3 A o45 1/21/2016 Velmurugan Sivaraman 21
- 22. 0.3 A A 0.3 Wide ToleranceZone A A Perpendicularity (Feature Surface to Datum Surface) 0.3 Wide Tolerance Zone The tolerance zone in this example is defined by two parallel planes oriented perpendicular to the datum reference plane. Perpendicularity is the condition of the planar feature surface at a right angle to the datum reference plane, within the specified tolerance zone. 1/21/2016 Velmurugan Sivaraman 22
- 23. C Perpendicularity (Feature Axis toDatum Surface) 0.3 C 0.3 Circular Tolerance Zone 0.3 Diameter Tolerance Zone 0.3 Circular Tolerance Zone NOTE: Tolerance applies to feature at RFS The tolerance zone in this example is defined by a cylinder equal to the length of the feature, oriented perpendicular to the datum reference plane. Perpendicularity is the condition of the feature axis at a right angle to the datum reference plane, within the specified tolerance zone. 1/21/2016 Velmurugan Sivaraman 23
- 24. 0.3 A A 25 +/-0.5 25.5max 0.3 Wide Tolerance Zone A 24.5 min 0.3 Wide Tolerance Zone A Parallelism (Feature Surface to Datum Surface) The tolerance zone in this example is defined by two parallel planes oriented parallel to the datum reference plane. Parallelism is the condition of the planar feature surface equidistant at all points from the datum reference plane, within the specified tolerance zone. 1/21/2016 Velmurugan Sivaraman 24
- 25. A 0.3 Wide Tolerance Zone Parallelism (FeatureAxis to Datum Surface) 0.3 A A NOTE: The specified tolerance does not apply to the orientation of the feature axis in this direction The tolerance zone in this example is defined by two parallel planes oriented parallel to the datum reference plane. Parallelism is the condition of the feature axis equidistant along its length from the datum reference plane, within the specified tolerance zone. NOTE: Tolerance applies to feature at RFS 1/21/2016 Velmurugan Sivaraman 25
- 26. A B Parallelism (Feature Axis toDatum Surfaces) A B 0.3 Circular Tolerance Zone 0.3 Circular Tolerance Zone 0.3 Circular Tolerance Zone The tolerance zone in this example is defined by a cylinder equal to the length of the feature, oriented parallel to the datum reference planes. Parallelism is the condition of the feature axis equidistant along its length from the two datum reference planes, within the specified tolerance zone. NOTE: Tolerance applies to feature at RFS 0.3 A B 1/21/2016 Velmurugan Sivaraman 26
- 27. Parallelism (Feature Axis toDatum Axis) Parallelism is the condition of the feature axis equidistant along its length from the datum reference axis, within the specified tolerance zone. A 0.1 A 0.1 Circular Tolerance Zone 0.1 Circular Tolerance Zone Datum Axis A The tolerance zone in this example is defined by a cylinder equal to the length of the feature, oriented parallel to the datum reference axis. NOTE: Tolerance applies to feature at RFS 1/21/2016 Velmurugan Sivaraman 27
- 28. Tolerances of Profile Profile ofa Line Profile of a Surface (ASME Y14.5M-1994, 6.5.2b) (ASME Y14.5M-1994, 6.5.2a) 1/21/2016 Velmurugan Sivaraman 28
- 29. Profile of aLine The profile tolerance zone in this example is defined by two parallel lines oriented with respect to the datum reference frame. The profile tolerance zone is free to float within the larger size tolerance and applies only to the form and orientation of any individual line element along the entire surface. 1/21/2016 Velmurugan Sivaraman 29
- 30. A 25 A0.5 0.1 25.25 24.75 0.1 Wide ToleranceZone A Composite Profile of Two Coplanar Surfaces w/o Orientation Refinement Profile of a Surface Form Only Location & Orientation 1/21/2016 Velmurugan Sivaraman 30
- 31. 0.1 Wide ToleranceZone 0.1 Wide Tolerance Zone 25.25 24.75 A A A 25 A0.5 A0.1 Form & Orientation Composite Profile of Two Coplanar Surfaces With Orientation Refinement Profile of a Surface Location 1/21/2016 Velmurugan Sivaraman 31
- 32. Tolerances of Location True Position Concentricity Symmetry 1/21/2016Velmurugan Sivaraman 32
- 33. 10.25 +/- 0.5 10.25+/- 0.5 8.5 +/- 0.1 Rectangular Tolerance Zone 10.25 10.25 8.5 +/- 0.1 Circular Tolerance Zone B A C Coordinate vs Geometric Tolerancing Methods Coordinate Dimensioning Geometric Dimensioning Rectangular Tolerance Zone Circular Tolerance Zone 1.4 +/- 0.5 +/- 0.5 57% Larger Tolerance Zone Circular Tolerance Zone Rectangular Tolerance Zone Increased Effective Tolerance 1.4 A B C 1/21/2016 Velmurugan Sivaraman 33
- 34. Formula to determinethe actual radial position of a feature using measured coordinate values (RFS) Z positional tolerance /2 X2 Y2 +Z = X Y Z Feature axis actual location (measured) Positional tolerance zone cylinder Feature axis true position (designed) Positional Tolerance Verification Z = total radial deviation Actual feature boundary (Applies when a circular tolerance is indicated) 1/21/2016 Velmurugan Sivaraman 34
- 35. Formula to determinethe actual radial position of a feature using measured coordinate values (MMC) Z X2 Y2 +Z = X =2 Y =2 X Y Z Feature axis actual location (measured) Positional tolerance zone cylinder Feature axis true position (designed) Positional Tolerance Verification Z = total radial deviation “X” measured deviation “Y” measured deviation Actual feature boundary +( actual - MMC) 2= positional tolerance (Applies when a circular tolerance is indicated) 1/21/2016Velmurugan Sivaraman 35
- 36. Bi-directional True Position RectangularCoordinate Method 3510 10 AC B 1.5 A B C 0.5 A B C2X 2X 10 35 1.5 Wide Tolerance Zone 0.5 Wide Tolerance Zone True Position Related to Datum Reference Frame 10 B C Each axis must lie within the 1.5 X 0.5 rectangular tolerance zone basically located to the datum reference frame As Shown on Drawing Means This: 2X 6 +/-0.25 1/21/2016Velmurugan Sivaraman 36
- 37. 3510 10 AC B As Shown onDrawing Means This: 1.5 A B C 0.5 A B C BOUNDARY BOUNDARY 10 35 10 B C 2X 13 +/-0.25 2X 6 +/-0.25 12.75 MMC width of slot -1.50 Position tolerance 11.25 Maximum boundary Both holes must be within the size limits and no portion of their surfaces may lie within the area described by the 11.25 x 5.25 maximum boundaries when the part is positioned with respect to the datum reference frame. The boundary concept can only be applied on an MMC basis. o 90 True position boundary related to datum reference frame A Bi-directional True Position Noncylndrical Features (Boundary Concept) MM 5.75 MMC length of slot -0.50 Position tolerance 5.25 maximum boundary 1/21/2016Velmurugan Sivaraman 37
- 38. Location (Concentricity) Datum Featuresat RFS A 15.95 15.90 As Shown on Drawing Derived Median Points of Diametrically Opposed Elements Axis of Datum Feature A Means This: Within the limits of size and regardless of feature size, all median points of diametrically opposed elements must lie within a Ø 0.5 cylindrical tolerance zone. The axis of the tolerance zone coincides with the axis of datum feature A. Concentricity can only be applied on an RFS basis. 0.5 A 6.35 +/- 0.05 0.5 Coaxial Tolerance Zone 1/21/2016Velmurugan Sivaraman 38
- 39. Location (Symmetry) Datum Featuresat RFS A 15.95 15.90 0.5 A 6.35 +/- 0.05 Derived Median Points Center Plane of Datum Feature A 0.5 Wide Tolerance Zone Means This: Within the limits of size and regardless of feature size, all median points of opposed elements must lie between two parallel planes equally disposed about datum plane A, 0.5 apart. Symmetry can only be applied on an RFS basis. As Shown on Drawing 1/21/2016Velmurugan Sivaraman 39
- 40. Tolerances of Runout Circular Runout (ASMEY14.5M-1994, 6.7.1.2.1) Total Runout (ASME Y14.5M-1994 ,6.7.1.2.2) 1/21/2016 Velmurugan Sivaraman 40
- 41. Datum feature Datum axis(established from datum feature Angled surfaces constructed around a datum axis External surfaces constructed around a datum axis Internal surfaces constructed around a datum axis Surfaces constructed perpendicular to a datum axis Features Applicable to Runout Tolerancing 1/21/2016Velmurugan Sivaraman 41
- 42. 0 + - Full Indicator Movement MaximumMinimu m Total Tolerance Maximum Reading Minimum Reading Full Part Rotation Measuring position #1 (circular element #1) Circular Runout When measuring circular runout, the indicator must be reset to zero at each measuring position along the feature surface. Each individual circular element of the surface is independently allowed the full specified tolerance. In this example, circular runout can be used to detect 2-dimensional wobble (orientation) and waviness (form), but not 3- dimensional characteristics such as surface profile (overall form) or surface wobble (overall orientation). Measuring position #2 (circular element #2) Circular runout can only be applied on an RFS basis and cannot be modified to MMC or LMC. 1/21/2016Velmurugan Sivaraman 42
- 43. o360 Part Rotation 50 +/-2 o o As Shown on Drawing Means This: Datum axis A Single circular element Circular Runout (Angled Surface to Datum Axis) 0.75 A A 50 +/-0.25 0 +- NOTE: Circular runout in this example only controls the 2-dimensional circular elements (circularity and coaxiality) of the angled feature surface not the entire angled feature surface Full Indicator Movement( ) The tolerance zone for any individual circular element is equal to the total allowable movement of a dial indicator fixed in a position normal to the true geometric shape of the feature surface when the part is rotated 360 degrees about the datum axis. The tolerance limit is applied independently to each individual measuring position along the feature surface. Allowable indicator reading = 0.75 max. When measuring circular runout, the indicator must be reset when repositioned along the feature surface. Collet or Chuck 1/21/2016 Velmurugan Sivaraman 43
- 44. 0 + Full Indicator Movement Total Tolerance Maximum Reading Minimu m Reading Full Part Rotation - 0 +- Total Runout Maximum Minimu m When measuring total runout, the indicator is moved in a straight line along the feature surface while the part is rotated about the datum axis. It is also acceptable to measure total runout by evaluating an appropriate number of individual circular elements along the surface while the part is rotated about the datum axis. Because the tolerance value is applied to the entire surface, the indicator must not be reset to zero when moved to each measuring position. In this example, total runout can be used to measure surface profile (overall form) and surface wobble (overall orientation). Indicator Path Total runout can only be applied on an RFS basis and cannot be modified to MMC or LMC. 1/21/2016Velmurugan Sivaraman 44
- 45. Full Part Rotation 50 +/-2 o o As Shown on Drawing A 50 +/-0.25 0.75 A Means This: Datum axis A 0 +- The tolerance zone for the entire angled surface is equal to the total allowable movement of a dial indicator positioned normal to the true geometric shape of the feature surface when the part is rotated about the datum axis and the indicator is moved along the entire length of the feature surface.0 +- NOTE: Unlike circular runout, the use of total runout will provide 3-dimensional composite control of the cumulative variations of circularity, coaxiality, angularity, taper and profile of the angled surface Total Runout (Angled Surface to Datum Axis) Collet or Chuck When measuring total runout, the indicator must not be reset when repositioned along the feature surface. (applies to the entire feature surface) Allowable indicator reading = 0.75 max. 1/21/2016 Velmurugan Sivaraman 45
- 46. 0 +- Total Runout (Surface Perpendicularto Datum Axis) As Shown on Drawing A 50 +/-0.25 0.75 A 35 10 0 +- Datum axis A Full Part Rotation 35 10 Means This: NOTE: The use of total runout in this example will provide composite control of the cumulative variations of perpendicularity (wobble) and flatness (concavity or convexity) of the feature surface. The tolerance zone for the portion of the feature surface indicated is equal to the total allowable movement of a dial indicator positioned normal to the true geometric shape of the feature surface when the part is rotated about the datum axis and the indicator is moved along the portion of the feature surface within the area described by the basic dimensions. When measuring total runout, the indicator must not be reset when repositioned along the feature surface. (applies to portion of feature surface indicated) Allowable indicator reading = 0.75 max. 1/21/2016 Velmurugan Sivaraman 46
- 47.
- 48. 2x M10 X1.5 (Reference) B A ?.? 2x 10.50 +/- 0.25 M Calculate Required Positional Tolerance 0.5 2x ??.?? +/- 0.25 M Calculate Nominal Size A B T = H - F H = Minimum Hole Size = 10.25 F = Max. Fastener Size = 10 T = 10.25 -10 T = ______ Floating Fasteners H = F +T F = Max. Fastener Size = 10 T = Positional Tolerance = 0.50 H = 10 + 0.50 H = ______ In applications where two or more mating details are assembled, and all parts have clearance holes for the fasteners, the floating fastener formula shown below can be used to calculate the appropriate hole sizes or positional tolerance requirements to ensure assembly. The formula will provide a “zero-interference” fit when the features are at MMC and at their extreme of positional tolerance H= Min. diameter of clearance hole F= Maximum diameter of fastener T= Positional tolerance diameter H=F+T or T=H-F General Equation Applies to Each Part Individually remember: the size tolerance must be added to the calculated MMC hole size to obtain the correct nominal value. 1/21/2016 Velmurugan Sivaraman 48
- 49. 2x M10 X1.5 (Reference) B A 0.25 2x 10.50 +/- 0.25 M 0.5 2x 10.75 +/- 0.25 M A B Floating Fasteners REMEMBER!!! All Calculations Apply at MMC H= Min. diameter of clearance hole F= Maximum diameter of fastener T= Positional tolerance diameter H=F+T or T=H-F General Equation Applies to Each Part Individually T = H - F H = Minimum Hole Size = 10.25 F = Max. Fastener Size = 10 T = 10.25 -10 T = 0.25 Calculate Required Positional Tolerance F = Max. Fastener Size = 10 T = Positional Tolerance = 0.5 H = 10 + .5 H = 10.5 Minimum H = F +T In applications where two or more mating details are assembled, and all parts have clearance holes for the fasteners, the floating fastener formula shown below can be used to calculate the appropriate hole sizes or positional tolerance requirements to ensure assembly. The formula will provide a “zero-interference” fit when the features are at MMC and at their extreme of positional tolerance remember: the size tolerance must be added to the calculated MMC hole size to obtain the correct nominal value. Calculate Nominal Size 1/21/2016 Velmurugan Sivaraman 49
- 50. F = Max.Fastener Size = 10.00 T = Positional Tolerance = 0.80 2x M10 X 1.5 (Reference) B A 0.8 2x ??.?? +/- 0.25 M Calculate Required Clearance Hole Size. 2X M10 X 1.5 A B Fixed Fasteners H = 10.00 + 2(0.8) H = _____ H= Min. diameter of clearance hole F= Maximum diameter of fastener T= Positional tolerance diameter H=F+2T or T=(H-F)/2 General Equation Used When Positional Tolerances Are Equal In fixed fastener applications where two mating details have equal positional tolerances, the fixed fastener formula shown below can be used to calculate the appropriate minimum clearance hole size and/or positional tolerance required to ensure assembly. The formula provides a “zero-interference” fit when the features are at MMC and at their extreme of positional tolerance. (Note that in this example the positional tolerances indicated are the same for both parts.) 0.8 M 10P APPLIES WHEN A PROJECTED TOLERANCE ZONE IS USED Nominal Size (MMC For Calculations) H = F + 2T remember: the size tolerance must be added to the calculated MMC size to obtain the correct nominal value. 10 1/21/2016Velmurugan Sivaraman 50
- 51. Surface finish Surface finishis a characteristic of any machined surface. It is sometimes called surface texture or roughness. The design engineer is usually the person that decides what the surface finish of a work piece should be. They base their reasoning on what the work piece is supposed to do. 1/21/2016Velmurugan Sivaraman 51
- 52.
- 53. Types of Surfacefinish? 1/21/2016 Velmurugan Sivaraman 53
- 54. 1/21/2016 Velmurugan Sivaraman54 Surface Texture Analysis of cylinder bore
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.