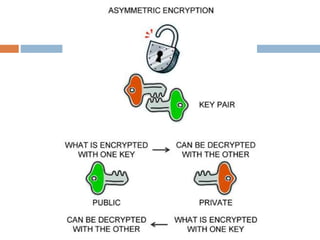
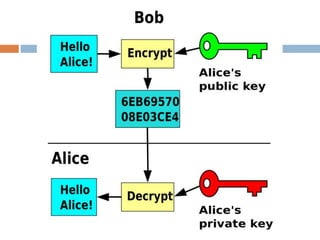
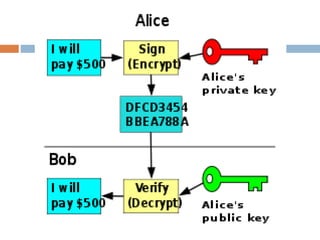
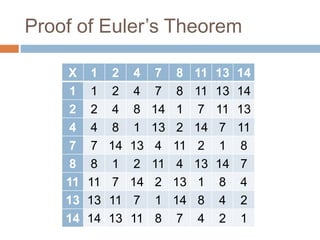
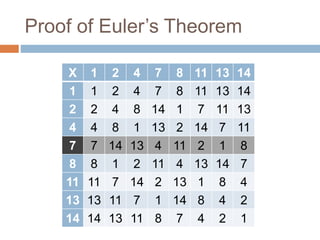
The document provides an overview of RSA encryption, explaining its functionality as a public key cryptography scheme. It delves into the mathematical principles behind RSA, such as modulus, prime factorization, Euler's theorem, and how to generate public and private keys. The document also discusses the security of RSA, emphasizing the challenges involved in deriving the private key from the public key and the difficulty of solving encrypted messages.

1. THE MATHEMATICS OF
RSA ENCRYPTION
Casco Bay .NET User Group
Nov. 2016

2. Goals
 Make encryption less mysterious

3. Outline
 What is RSA Encryption?
 Math Refresher
 How does it work?
 Math Deep Dive
 Where do keys come from?
 Why does it work?
 Why is it secure?

4. What is RSA Encryption?
 Public Key Cryptography Scheme

8. Math Refresher - Modulus
 %
 “The Remainder” operator
 546 % 31 = 19
 546 = 17*31 + 19

9. Math Refresher - Primes
 A prime can only be divided by 1 and itself
 Every number can be factored into a list of
primes
 360 = 2 * 2 * 2 * 3 * 3 * 5
 11 = 11
 Two numbers are coprime if they have no
common prime factors
 6 = 2 * 3, 35 = 5 * 7, so 6 and 35 are coprime
 26 = 2 * 13, 4 = 2 * 2, so 26 and 4 are not
coprime

10. How Does it Work?
 Public key: (e, n)
 Private key: (d, n)
 Message: M
 Encrypted Message: EM = M**e % n
 Decrypted Message: DM = EM**d % n

11. Example
 Public key: (e, n) = (3593, 150349)
 Private key: (d, n) = (957, 150349)
 Message: M = 90001
 Encrypted Message: EM = M**e % n
 EM = 90001**3593 % 150349
 131425
 Decrypted Message: DM = EM**d % n
 DM = 131425**957 % 150349
 90001

12. Example
 Public key: (e, n) = (3593, 150349)
 Private key: (d, n) = (957, 150349)
 Message: M = 22621
 Encrypted Message: EM = M**e % n
 EM = 22621**3593 % 150349
 62033
 Decrypted Message: DM = EM**d % n
 DM = 62033**957 % 150349
 22621

13. Why did that work?

14. Why did that work?
 Math

15. Why did that work?
 Math
 Cleverly chosen keys

16. Why did that work?
 Math
 Cleverly chosen keys
 Euler’s Theorem

17. φ, the totient function
 φ(n) is called the totient of n
 Number of integers less than n, coprime with n
 n = 15 = 5 * 3
 φ(15) = Number of integers coprime with 15
 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
 1, 2, 4, 7, 8, 11, 13, 14
 φ(15) = 8

18. Calculating φ(n)
 φ(15) = 8
 Notice: φ(5 * 3) = (5-1) * (3-1)
 n = p * q
 n is the product of 2 different primes, p and q
 There are p multiples of q
 There are q multiples of p
 0 is counted twice
 φ(n) = p*q – p – q + 1 = (p-1) * (q-1)

19. Euler’s Theorem
 x**φ(n) % n = 1, where x is coprime with n
 Euler’s Theorem predicts x**8 % 15 = 1
 For x coprime with 15
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 1 1 6 1 10 6 1 1 6 10 1 6 1 1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0 1 1 6 1 10 6 1 1 6 10 1 6 1 1
1 2 4 7 8 11 13 14
1 1 1 1 1 1 1 1

20. Proof of Euler’s Theorem
X 1 2 4 7 8 11 13 14
1 1 2 4 7 8 11 13 14
2 2 4 8 14 1 7 11 13
4 4 8 1 13 2 14 7 11
7 7 14 13 4 11 2 1 8
8 8 1 2 11 4 13 14 7
11 11 7 14 2 13 1 8 4
13 13 11 7 1 14 8 4 2
14 14 13 11 8 7 4 2 1

21. Proof of Euler’s Theorem
X 1 2 4 7 8 11 13 14
1 1 2 4 7 8 11 13 14
2 2 4 8 14 1 7 11 13
4 4 8 1 13 2 14 7 11
7 7 14 13 4 11 2 1 8
8 8 1 2 11 4 13 14 7
11 11 7 14 2 13 1 8 4
13 13 11 7 1 14 8 4 2
14 14 13 11 8 7 4 2 1

22. Proof of Euler’s Theorem
 Consider the product of each number in the
first row
 1*2*4*7*8*11*13*14 % 15
 What if we multiply this value by 7**8?
 7**8 * (1*2*4*7*8*11*13*14) % 15
 (7*1)*(7*2)*(7*4)*(7*7)*(7*8)*(7*11)*(7*13)*(7*14)
% 15
 7*14*13*4*11*2*1*8 % 15
 1*2*4*7*8*11*13*14 % 15
 It didn’t change the value, so 7**8 % 15 = 1

23. Key Generation
 How did we get our keys from the example?
 Public key: (e, n) = (3593, 150349)
 Private key: (d, n) = (957, 150349)

24. Key Generation
 p, q = 251, 599
 n = p * q
 150349
 e = 3593
 φ(n) = (p-1) * (q-1)
 149500
 d*e % φ(n) = 1 solve for d
 d*3593 % 149500 = 1
 d = 957 is the only solution

25. What makes those keys work?
 EM = M**e % n
 DM = EM**d % n
 DM = (M**e % n)**d % n
 DM = M**(e * d) % n

26. Why does it work?
 DM = M**(e*d) % n
 e*d % φ(n) = 1
 e*d = 1 + k*φ(n)
 DM = M**(1 + k*φ(n)) % n
 = (M**1) * (M**φ(n))**k % n
 = M * (1**k) % n
 = M

27. Why is it secure?
 Can we get the private key from the public
key?
 e*d % φ(n) = 1
 3593*d % φ(150349) = 1

28. Why is it secure?
 Can we get the private key from the public
key?
 e*d % φ(n) = 1
 3593*d % φ(150349) = 1
 No, because factoring appears to be difficult

29. Why is it secure?
 Can we get the private key from the public
key?
 e*d % φ(n) = 1
 3593*d % φ(150349) = 1
 No, because factoring appears to be difficult
 RSA-200
 279978339112213278708294676387226016210
704467869554285375600099293261284001076
093456710529553608560618223519109513657
886371059544820065767750985805576135790
987349501441788631789462951872378692218

30. Why is it secure?
 Can we solve for M given the encrypted
message?
 EM = M**e % n
 131435 = M**3593 % 150349

31. Why is it secure?
 Can we solve for M given the encrypted
message?
 EM = M**e % n
 131435 = M**3593 % 150349
 No, because taking the eth root (The RSA
Problem) appears to be difficult

32. Why is it secure?
 Can we solve for d given a decrypted
(authenticated) message?
 EM = M**d % n
 131435 = 90001**d % 150349

33. Why is it secure?
 Can we solve for d given a decrypted
(authenticated) message?
 EM = M**d % n
 131435 = 90001**d % 150349
 No, because the discrete logarithm appears to
be difficult

34. Why is it secure?
 Can we take a guess at M, given the
encrypted message?
 EM = M**e % n
 131435 = M**3593 % 150349

35. Why is it secure?
 Can we take a guess at M, given the
encrypted message?
 EM = M**e % n
 131435 = M**3593 % 150349
 90001**3593 % 150329 = 131435 !!

36. Why is it secure?
 Can we take a guess at M, given the
encrypted message?
 EM = M**e % n
 131435 = M**3593 % 150349
 90001**3593 % 150329 = 131435 !!
 Yes, that is a “chosen plaintext attack”, and
that is why you must pad your messages

37. More References
 Video demonstrating Public Key Cryptography
 https://www.youtube.com/watch?v=GSIDS_lvRv4
 Wikipedia Page
 https://en.wikipedia.org/wiki/RSA_(cryptosystem)

38. Appendix: Properties of %
 A + B % n = (A % n) + (B % n) % n
 517 + 878 % 10 = 7 + 8 % 10
 A * B % n = (A % n) * (B % n) % n
 318 * 73 % 10 = 8 * 3 % 10
 A ** B % n = (A % n) ** B % n ≠ (A % n) ** (B
% n)
 93 ** 57 % 10 = 3 ** 57 % 10 ≠ 3 ** 7 % 10
 A ** B % n = A ** (B % phi(n)) % n
 (For A and n coprime)
 93 ** 57 % 10 = 93 ** (57 % 4) % 10
 A % n = A’ => A = A’ + k*n