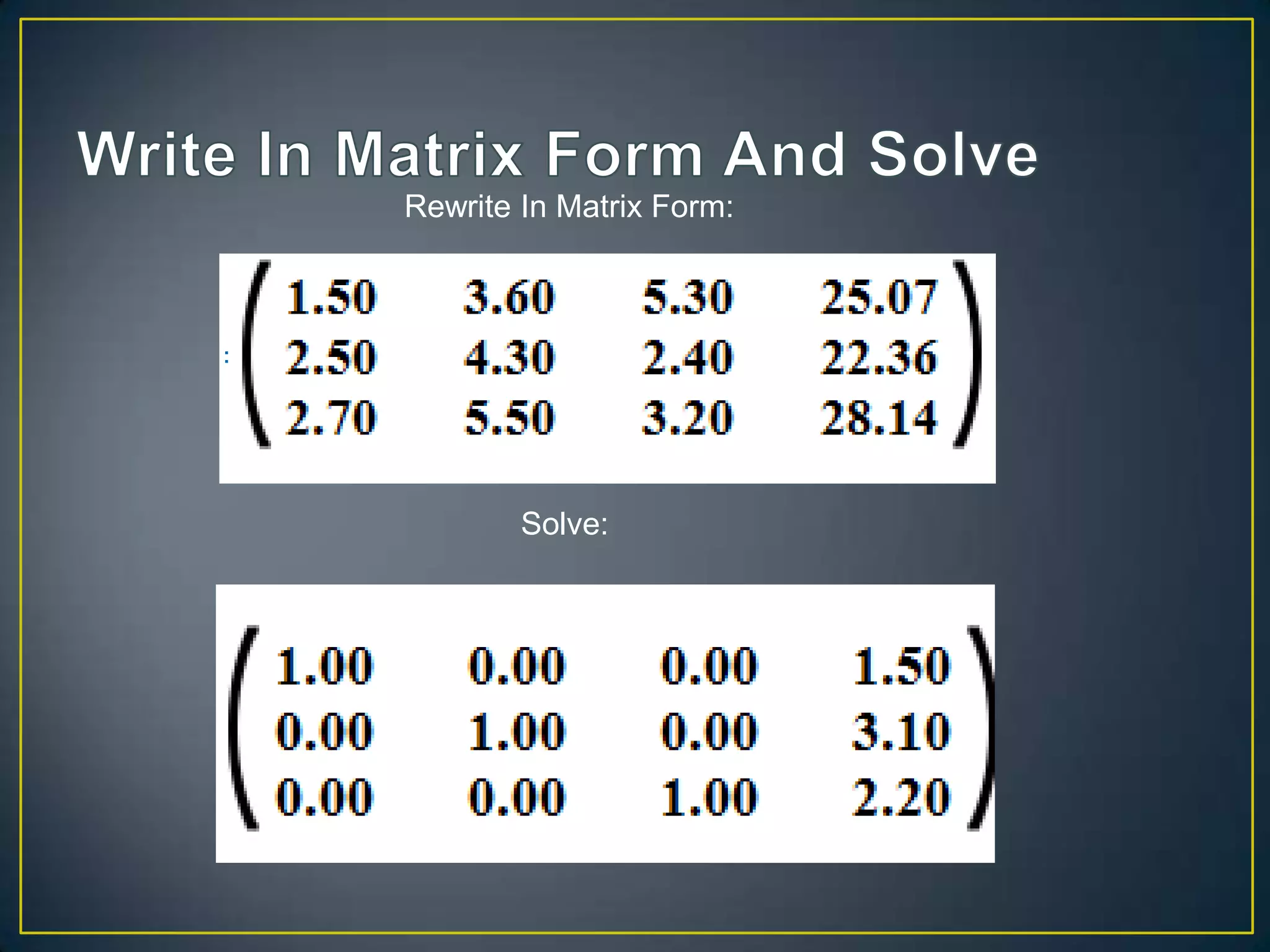
The document discusses using linear algebra to solve chemistry problems involving balancing chemical equations and determining volumes of chemical solutions. It provides an example of using a system of equations represented in matrix form to determine that the volumes of solutions A, B, and C are 1.5 cm3, 3.1 cm3, and 2.2 cm3 based on the amounts of chemical produced under different concentration conditions. The document also demonstrates how to use the law of conservation of matter and a similar technique to balance the chemical equation C2H6 + O2 → CO2 + H2O.

1. Anish Jain

2. • Linear Algebra required for chem. majors
• Useful for balancing chemical equations
• Can solve basic math problems in chemistry
• Martin Cockett, Graham Doggett
• Discuss and teach these uses

3. Question:
It takes three different ingredients A, B, and C, to produce a
certain chemical substance. A, B, and C have to be dissolved in
water separately before they interact to form the chemical.
Suppose that the solution containing A at 1.5 g/cm3 combined
with the solution containing B at 3.6 g/cm3 combined with the
solution containing C at 5.3 g/cm3 makes 25.07 g of the
chemical. If the proportion for A, B, C in these solutions are
changed to 2.5 g/cm3, 4.3 g/cm3, and 2.4 g/cm3, respectively
(while the volumes remain the same), then 22.36 g of the
chemical is produced. Finally, if the proportions are 2.7
g/cm3, 5.5 g/cm3, and 3.2 g/cm3, respectively, then 28.14 g of the
chemical is produced. What are the volumes (in cubic
centimeters) of the solutions containing A, B, and C?

4. Simplified Version:
• Three Ingredients A,B,C
• Defined by fixed volume
• 1.5 g/cm3 of A + 3.6 g/cm3 of B+ 5.3 g/cm3 of C= 25.07 g
• 2.5 g/cm3 of A + 4.3 g/cm3 of B+ 2.4 g/cm3 of C= 22.36 g
• 2.7 g/cm3 of A + 5.5 g/cm3 of B+ 3.2 g/cm3 of C= 28.14 g

5. • Represent volumes with a, b, and c respectively:
• 1.5 a+ 3.6 b+ 5.3 c= 25.07
• 2.5 a+ 4.3 b+ 2.4 c= 22.36
• 2.7 a+ 5.5 b+ 3.2 c= 28.14

6. Rewrite In Matrix Form:
Solve:

7. • Converting back to equation form:
• a=1.5cm3, b=3.1cm3, c=2.2cm3
• Demonstrates use of linear algebra for simple chemistry
problem

8. • Linear Algebra can be used to balance chemical
equations
• Law of Conservation of Matter:
• Mass is neither created nor destroyed in any chemical reaction.
Therefore balancing of equations requires the same number of
atoms on both sides of a chemical reaction. The mass of all the
reactants (the substances going into a reaction) must equal the
mass of the products (the substances produced by the reaction).

9. Question:
Balance the chemical equation xC2H 6 + yO2 →
zCO2 + tH2O
by finding out how much of each molecule is needed to
satisfy the Law of Conservation of Matter. The amount of
each molecule needed is represented by x, y, z, and t.

10. The amount of each type of atom is written in parentheses:
(2x)C+(6x)H+(2y)O=(z)C+(2z)O+(2t)H+(t)O
We can break this down into three equations by matching
them up by the atom:
• 2x=z
• 6x=2t
• 2y=2z+t

11. First rewrite equations:
• 2x-z=0
• 6x-2t=0
• 2y-2z-t=0
Write in Matrix Form:

12. Can simplify matrix to:
Writing back in equation form:
• x=2/6t
• y=7/6t
• z=2/3t
• t=1t

13. • t can be any real number and equation would be
balanced
• However, small integer numbers are preferred
• Set t=6:
2C2H 6 + 7O2 → 4CO2 + 6H2O