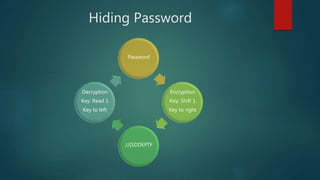
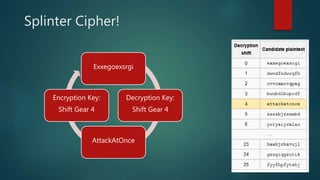
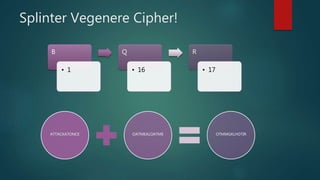
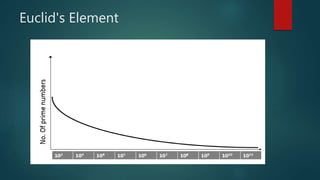
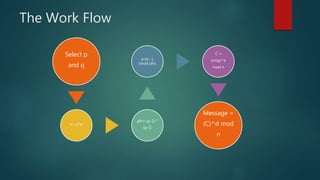
This document provides an introduction to cryptography. It discusses how cryptography is essential for secure communication on the internet. It then covers the history of cryptography from its first documented uses in ancient Egypt through its importance in World War II. It defines cryptography terms and describes encryption and decryption. It also summarizes some classical cryptography techniques like the Caesar cipher and discusses concepts like prime numbers and the RSA encryption algorithm.

1. Cryptography

2. An Introduction
"The art of writing and solving codes"
Internet provides essential communication between tens of millions of
people and is being increasingly used as a tool for commerce, security
becomes a tremendously important issue to deal with.
There are many aspects to security and many applications, ranging from
secure commerce and payments to private communications and protecting
passwords. One essential aspect for secure communications is that of
cryptography. But it is important to note that while cryptography is
necessary for secure communications, it is not by itself sufficient.

3. Antiquity
 The first documented use of cryptography in writing dates back to
Circa 1900 BC when an Egyptian scribe used non standard hieroglyphs
in an inscription. Some experts argue that cryptography appear
spontaneously sometimes after writing was invented with applications
ranging from diplomatic missives to war-time battle plans.
 Its real era started from World War II when Germany was about to
take over Great Britain, Germany used a device named "Enigma" to
send their messages secretly to their war zones. In reply GBR created
a device named "Turing Machine" by Alan Turing to decrypt or break
Enigma which resulted in saving GBR.

4. Greek Etymology
 Cryptography
- Crypto -----> "Kryptos" --------> Hidden
- Graphy -----> "Graphein" -------> To Write
Encryption: The translation of data into secret
code.
Decryption: The translation of secret code into
original data.

5. The Caesar Cipher!
Plaintext: THE QUICK BROWN FOX JUMPS OVER THE LAZY DOG
Ciphertext: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
 Encryption:
E(x) = (x + n) mod 26
 Decryption:
D(x) = (x - n) mod 26

6. Hiding Password
Password
Encryption
Key: Shift 1
Key to right
,U[SDDEPTF
Decryption
Key: Read 1
Key to left

7. Splinter Cipher!
Exxegoexsrgi
Decryption Key:
Shift Gear 4
AttackAtOnce
Encryption Key:
Shift Gear 4

8. Splinter Vegenere Cipher!
B
• 1
Q
• 16
R
• 17
ATTACKATONCE OATMEALOATME OTMMGKLHDTIR

9. What in the world is OTP?

10. Prime Numbers!
How to find a Prime Number?
Immortal are Prime Numbers.
Prime Numbers and Cryptography.
New Prime Number??

11. Methods to find
Prime Numbers
A Multiplicative
Sieve
The Prime
Number Machine
The Sieve of
Erastothenes

12. The Sieve of Erastothenes
Let's consider a table of sequential numbers
start
2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21
,22,23,24,25,26,27,28,29,30,31,32....

13. The Sieve of Erastothenes
Cross out multiple of 2
2, 3, X, 5, X, 7, X, 9, X, 11, X, 13....

14. The Sieve of Erastothenes
The next non-overlined and non crossed out
number is three. Identify it as prime with an
overline, then cross out every third number
(every multiple of three).
2, 3, X, 5, XX, 7, X, X, X, 11, XX, 13 ...

15. The Sieve of Erastothenes
Continuing the process. Five is the next non-
overlined and non crossed out number. Overline
five and cross out every fifth number.
2, 3, X, 5, XX, 7, X, X, X, 11, XX, 13 ...

16. The Sieve of Erastothenes
The next prime number is then seven. Since
twice seven is greater than the largest visible
number in our list, all the remaining visible
numbers are prime.
2, 3, X, 5, XX, 7, X, XX, X, 11, XX, 13 ...

17. The Sieve of Erastothenes
Drawbacks
 The process is too slow
 Not efficient for finding huge primes.

18. Euclid’S Element
 The statement says that
“There are more than any finite number n of prime
numbers. Suppose that a1, a2, ..., an are prime numbers. Let
m be the product of all considered prime numbers. Consider
the number m + 1. If it's prime, then there are at least n + 1
primes.”
 So suppose m + 1 is not prime. Then, some prime g divides it.
But g cannot be any of the primes a1, a2, ..., an , since they
all divide m and do not divide m + 1. Therefore, there are at
least n + 1 primes.
 Thus, there are not a finite number of primes.

19. Euclid's Element

20. RSA
How to make sure that my data is save on the internet?
How to make sure that only an authorized person gets
my secret message?
The RSA model is the correct choice!
RSA Stands for Ron Rivest, Adi Shamir , Leonard
Adleman.

21. RSA
RSA is a consequence of Fermat's little theorem:
"If 'a' is not divisible by 'p' , where p is prime,
then a^(p-1) -1 is divisible by 'p'.

22. The Work Flow
 Generate two large random prime numbers p and q
 Find n = p*q
 Find phi = (p-1)*(q-1)
 Choose an integer e, 1 < e < phi such that GCD (e, phi) = 1
 Compute the secret exponent d, 1 < d < phi, such that e.d = 1
(mod phi)
 The public key is (n, e) and the private key is (d, p, q)
 All the values d, p, q and phi are kept secret.

23. The Work Flow
Select p
and q
n= p*q
phi= (p-1) *
(q-1)
e*d= 1
(mod phi)
C =
(msg)^e
mod n
Message =
(C)^d mod
n

24. Example
 P = 3 and Q = 11
 n = p*q = 33
 Phi = (p-1) * (q-1) = (3-1) * (11-1) = 20
 e = 7 and d =3 -------------> (3*7) mod 20 = 1
 Public Key (7, 33) and Private Key (3, 33)
 m = 13
 Encrypt: c = m^e mod n -------> c = 13^7 mod 33 = 7
 Decrypt: m = c^d mod n ---------> 7^8 mod 33 = 13

25. • How to break RSA?
• First we have to find p and q
• Solve the equation to find 'd'

26. Why is it difficult to get the decryption key?
Factoring the huge number to prime
number takes a lot of computation
Then there can be number of multiples of
N, so might be guessing on wrong number.

27. Presented By
Talha Saleem
Mohammad Owais