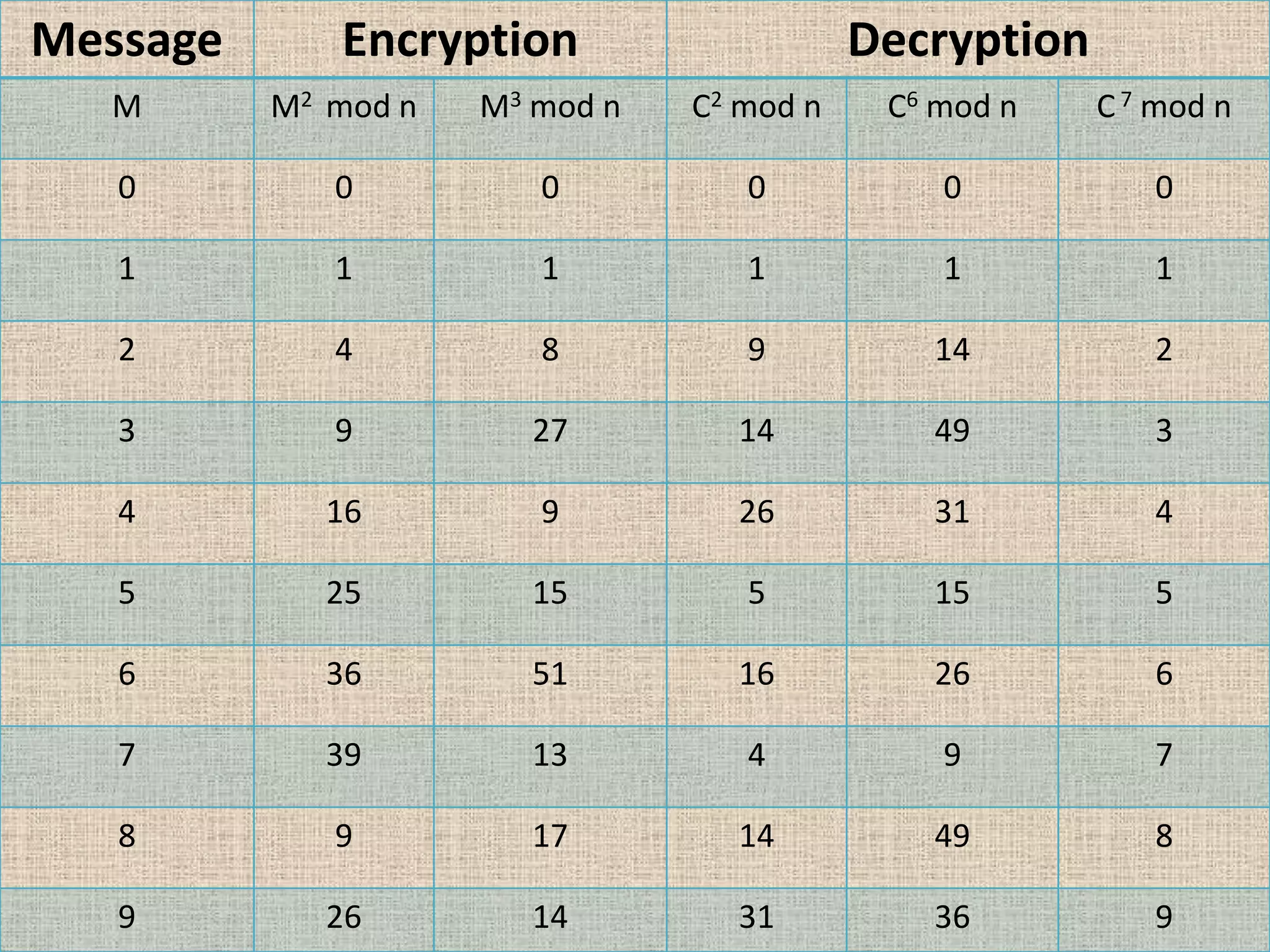
The document provides a comprehensive overview of data, information security, and cryptography, focusing particularly on the RSA cryptosystem. It explains key concepts such as data representation, the role of information security in maintaining confidentiality, integrity, and availability, as well as the mechanics of RSA encryption and decryption using key pairs. The conclusion emphasizes the widespread use and resilience of RSA in cryptographic applications.

2. Contents
 Understanding Data & Information
 What is Information Security?
 What is Cryptography?
 RSA cryptosystem
Introduction
 Key generation Algorithm
Encryption & Decryption
Key Pair Generation Example
 Implementation
 Limitation
 Conclusion
 Reference

3. Understanding Data &
Information
What is Data?
 Data can be defined as a representation of facts, concepts
or instructions in a formalized manner, which should be
suitable for communication, interpretation or processing by
human or electronic machine.
What is Information?
 Information is organized or classified data so that it has
some meaningful values to the receiver.
 Information is the processed data on which decisions and
actions are based.
 For the decision to be meaningful, the processed data must
be accurate, complete and in time.

4. What is Information Security?
Information Security is simply the process of keeping
information secure, protecting its confidentiality
availability, integrity, and non-repudiation.
Information Security Goals
 Confidentiality - protecting information from being
disclosed to unauthorized parties.
 Integrity - protecting information from being changed by
unauthorized parties.
 Availability - to the availability of information to authorized
parties only when requested.
 Non-repudiation - to confirm that the data is not
abandoned

5. What is Cryptography?
 It is the art of protecting information by transforming it
(encrypting it) into an unreadable format, called cipher
text.
 Only those who possess a secret key can decipher (or
decrypt) the message into plain text.
 Cryptography systems can be broadly classified into
1. Symmetric Key System
Uses a single secret key to encrypt and decrypt
Ex-Data Encryption Standard(DES)
2. Asymmetric Key system
Uses a public key(known to everyone ) for encryption
and a private key(known to recipient) for decryption.
Ex-RSA, ECDSA (Elliptic Curve Digital Signature
Algorithm), DSA (the Digital Signature Algorithm)

6. RSA Cryptosystem
 RSA is an algorithm for public-key cryptography.
 RSA stands for Ron Rivest, Adi Shamir and Leonard
Adleman(the publishers of the algorithm)
 The RSA cryptosystem assumes that multiplying two
numbers is a simple process.
 But factoring the products back into the original two
numbers is quite difficult to do computationally.
 The difficulty increases as we use larger and larger
numbers.

7. Introduction
 The system works on a public and private key system. The
public key is made available to everyone.
 With this key a user can encrypt data but cannot decrypt it.
 The only person who can decrypt it is the one who
possesses the private key.
 It is theoretically extremely difficult to generate the private
key from the public key.
 This makes the RSA algorithm a very popular choice in data
encryption

8. Key Generation Algorithm
 Choose two large random prime integers:
Take p and q
 Compute n and φ(n):
n = pq and φ(n) = (p-1)(q-1)
 Choose an odd public exponent e, 1 < e < φ(n) such that:
gcd(e, φ(n)) = 1
 Compute the private exponent d, 1 < d < φ(n) such that:
ed ≡ 1 (mod φ(n))

9. Key Generation Algorithm
 The public key is (n, e) and the private key is (n, d)
 The values of p, q and φ(n) are private.
 e is the public or encryption exponent.
 d is the private or decryption exponent.

10. Encryption & Decryption
Encryption
 The encryption operation in the RSA cryptosystem is
exponentiation to the e th power modulo n:
c = ENCRYPT (m) = me mod n
 The input m is the message.
 The output c is the resulting cipher text.
Decryption
 The decryption operation is exponentiation to the d th
power modulo n:
 The message m can be found form the cipher text C by the
equation
m = DECRYPT (c) = Cd mod n

11. Key Pair Generation
Example
 Take Primes:
p = 5, q = 11
 Compute n:
n = pq = 55
 Compute φ(n):
φ(n) = (p-1)(q-1)=40
 Choose Public exponent e = 3:
Check gcd(3,40)=1
 Compute Private exponent d:
d = 1/3 mod 20 = 7

12. Message Encryption Decryption
M M2 mod n M3 mod n C2 mod n C6 mod n C7 mod n
0 0 0 0 0 0
1 1 1 1 1 1
2 4 8 9 14 2
3 9 27 14 49 3
4 16 9 26 31 4
5 25 15 5 15 5
6 36 51 16 26 6
7 39 13 4 9 7
8 9 17 14 49 8
9 26 14 31 36 9

13. Implementation
 This technique is widely being used on the
internet, military, government sites in addition to banks
and other financial institutions.
 Also it is being used for
Disk encryption
Safe transformation of E-mail
Authentication process
Electronic Commerce

14. Limitation of RSA
Though so far RSA has not been broken but certain
attention must be given in the following cases
 Not using small primes.
( because N could be easily factorised)
 Not using primes that are very close.
(root of N will reveal how close they are)
 Two people must not use the same N.
(if the two public exponents are co-prime, then the
message may be retrieved)
 Message should not be observable of e th power.
(if the value of e is very small, then it is easy to find m)

15. Conclusion
 It is one of the most heavily used asymmetric cryptographic
algorithms in the world make it the envy and the favorite of
many security professionals.
 While the mathematics behind the algorithm are simple
enough to be relatively easily understood, the complexity
of dealing with very large prime numbers and the factoring
of even larger numbers into those primes is what makes
this encryption standard so resilient.

16. Reference
 http://www.tutorialspoint.com/computer_fundamentals/c
omputer_data.htm
 http://www.infosec.gov.hk/english/information/what.html
 http://idrbtca.org.in/inf_crypto.htm
 http://www.webopedia.com/TERM/C/cryptography.html
 http://www.dwhenry.com/files/RSA.pdf
 http://www.mathaware.org/mam/06/Kaliski.pdf