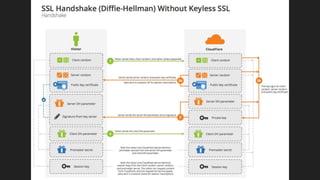
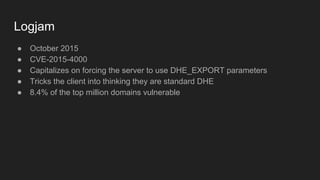
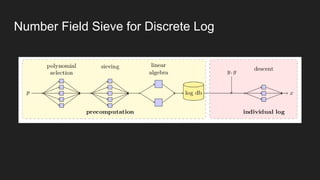
The document provides an overview of asymmetric cryptography, detailing its importance for confidentiality, integrity, authentication, and nonrepudiation. It focuses on RSA and Diffie-Hellman key exchange methods, their key generation processes, uses, and the vulnerabilities associated with public key cryptography. Additionally, it discusses historical milestones in cryptography, notable attacks, and future events related to pentesting and capture-the-flag competitions.

1. Asymmetric Cryptography
February 8, 2017

2. Why Cryptography?
● Confidentiality - only intended parties can read contents
● Integrity - message tampering can be detected
● Authentication - the author is verified
● Nonrepudiation - the author cannot deny being the author

3. Why asymmetric cryptography?
● No need to secretly distribute key
● Difficult to brute-force
● Reuse of key does not significantly weaken security

4. Why not asymmetric cryptography?
● More computationally-intensive than symmetric
cryptography

5. RSA
● Developed by Rivest, Shamir, and Adleman in 1977
● Based on the difficulty of factoring product of 2 large
primes, being able to compute private key from public key
● Built-in confidentiality, authentication, integrity, and
nonrepudiation from owner
● Computationally expensive

6. RSA Keys
● Public and private key should be prime numbers ≥ 2048
bits
● Public key should be available to everyone
○ Ex) Distribute using keyserver
● Private key should be known only to the owner of key pair

7. Key Generation and
Encryption/Decryption

8. RSA Key Generation
1. Pick primes of similar length (p = 61, q = 53)
2. Compute N as p x q (61 x 53 = 3233)
3. Compute the totient of N (60 x 52 = 3120)
4. Chose public exponent e that is coprime to N (17)
5. Compute the modular multiplicative inverse of e mod totient(N) (2753)

9. RSA Encryption
● e(m) = me
mod N = c
● d(c) = cd
mod N = m
Because:
● d(me
) = med
mod N = m -- ed = 1 + hφ(n) (Definition of multiplicative inverse)
● m1 + hφ(n)
mod N = m
● m(mφ(n)
)h
mod N = m -- aφ(n)
= 1 mod N (Euler’s Theorem)
● m(1)h
mod N = m

10. Uses for RSA
● First connection in SSL/TLS
● Signing communication
○ More efficient to encrypt hash of message rather than
whole message
● Subscription-based services like commercial TV, radio,
etc.

11. Diffie-Hellman Key Exchange
● Developed and published by Whitfield Diffie and Martin
Hellman in 1976
● Relies on difficulty of discrete logarithm problem
● Forward secrecy
● Can be performed with more than two parties
● More efficient than RSA

12. Diffie-Hellman Keys
● Communicating parties agree on a exponential base (g)
and prime modulus (p)
● Each communicating party generates a secret value to
use for exponentiation
● Shared symmetric key can be generated securely over
public network
○ Negotiation steps, if captured, should not give away
key

14. Key Generation and
Encryption/Decryption

15. Diffie Hellman Key Exchange
1. Alice and Bob agree on p = 23 and g = 5 (which is primitive root mod 23)
2. Alice chooses a = 6, and sends Bob A = 56
mod 23 = 8
3. Bob chooses b = 15, and sends Alice B = 515
mod 23 = 19
4. S = Ab
mod p = 815
mod 23 = 2
5. S = Ba
mod p = 196
mod 23 = 2

16. Uses for Diffie-Hellman
● Key negotiation over public or unsecured channels
(especially Ephemeral Diffie-Hellman)
○ Part of SSL/TLS
○ IPSec/VPN
○ SSH

17. Attacks on Public Key Cryptography

18. Timeline of “Modern” Cryptography
Post World War II - Cryptography is regulated as munitions (can’t be exported)
1975 - DES Published
1976 - Diffie-Hellman Key Exchange published
1977 - RSA published
1977 - DES Standardized (FIPS)
1985 - Amiga 1000 released
1989 - Public commercial use of the internet
1991 - PGP Released (First major instance of personal cryptography)
1993 - PGP finds it way out of the United States
1996 - Bernstein v. United States (Cryptography Export laws)
1996 - SSLv3 released (containing export grade cryptography)

20. Factoring RSA Export Keys
● FREAK
● March 3, 2015
● CVE-2015-0204
● Capitalizes on forcing the server to use RSA_EXPORT keys
● RSA_EXPORT Keys are 512 bits or less
● RSA_EXPORT keys were designed to be a backdoor, good enough for public
use, bad enough for the NSA to be able to break if needed
● 9.6% of top million domains vulnerable

21. Factoring RSA Export Keys
● Man in the Middle attack that requests RSA_EXPORT keys
● Most servers just go with it
● Most clients just go with it
● Generally one RSA_EXPORT key per server
● As seen in the diagram, knowing the premaster secret breaks the session

22. CADO-NFS
● Implementation of Number Field Sieve
● Current fastest way to factor large numbers
● Current fastest way to compute discrete logarithm
● Can break 512 bit RSA keys in 7 hours for ~$100 on EC2

24. Logjam
● October 2015
● CVE-2015-4000
● Capitalizes on forcing the server to use DHE_EXPORT parameters
● Tricks the client into thinking they are standard DHE
● 8.4% of the top million domains vulnerable

26. Number Field Sieve for Discrete Log

27. “Mining your P’s and Q’s”
● Low entropy RSA keys may share a common prime
● This prime can be found trivially with Euclid’s GCD Algorithm
● Finding one prime makes the other trivial to find, making generating a private
key trivial to find

28. Euclidean Algorithm for GCD
function gcd(a, b)
while b ≠ 0
t := b;
b := a mod b;
a := t;
return a;

29. More Resources:
● https://www.id0-rsa.pub/ - Cryptography Challenges
● https://www.youtube.com/watch?v=2aHkqB2-46k - Cryptography Lectures
● https://weakdh.org - Logjam Website
● https://mitls.org/pages/attacks/SMACK#freak - Freak Website
● https://factorable.net/ - Mining your P’s and Q’s
● https://github.com/kulinacs/smashcipher - Factor RSA library

30. Questions?

31. Future Events
● Introduction to Pentesting - Saturday, February 11th, 12 PM - 3 PM
● Coming up in March: Binary Exploitation
● CTFs for the semester (subject to change):
○ Boston Key Party (February 25th & 26th)
○ VolgaCTF (March 24th - 26th)
○ ASIS CTF (April 7th - 9th)