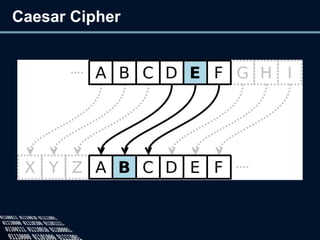
The document provides an overview of cryptography, defining it as the practice of secure communication and outlining its two main branches: private key and public key cryptography. It explains private key cryptography with examples like the Caesar cipher and techniques for cracking it, while also detailing public key cryptography, particularly RSA, including its key generation process. The document emphasizes the importance of mathematics in cryptographic techniques and the need for key secrecy.

1. Introduction to
Cryptography
by Petre POPESCU

2. What is cryptography?
"the art of hiding information"
OR
"the practice and study of techniques for secure
communication in the presence of third parties"
(wikipedia)

3. Modern Cryptography
a branch of mathematics
and
computer science

4. Modern Cryptography
2 main branches
1. Private Key Cryptography
2. Public Key Cryptography

5. Private Key Cryptography
The same key is used for both
encryption and decryption

6. Private Key Cryptography
Examples:
- DES
- AES
- Caesar Cipher
- Blowfish

7. Caesar Cipher
Named after Julius Caesar, who used it
in his private and military
correspondence.

8. Caesar Cipher
It is a substitution cipher
Each letter is replaced by another letter
depending on a "shift" value

9. Caesar Cipher

10. Cracking Caesar Cipher
(assuming we know Caesar Cipher is used)
1. Brute Force Attack
2. Word-pattern and letter distribution
attack

11. Brute Force Attack
Since the number of possible shifts is
limited, it is feasible to try each shift
and discard the results that are not
human readable.

12. Word-pattern and letter distribution attack
Step 1:
Find the average distribution of letter
in that language.
This can be done with ease by
analyzing long texts.

13. Word-pattern and letter distribution attack
Step 2:
A Caesar Cipher usually "shifts" this
distribution by the shift used for
encryption.
An error margin is permitted, so now
multiple possibilities are generated.

14. Word-pattern and letter distribution attack
Step 3:
Decrypt the text using the possible
shifts that were found in step 2.
Use word-pattern analysis (and
possibly a dictionary of words) to
discover the correct variant

15. Public Key Cryptography
Two keys are needed:
- one for encrypting the message
- one for decrypting the message

16. Public Key Cryptography
Key's properties
- neither keys can perform both
operations
- the two keys are mathematically
paired
- public key - used for encryption
- private key - used for decryption

17. Public Key Cryptography
Examples:
- RSA
- YAK
- Various elliptic curve techniques

18. RSA
Created by:
Ron Rivest
Adi Shamir
Leonard Adleman
Is based on the presumed difficulty of
factoring large integers.

19. RSA - Generating the two keys
(1) Choose two distinct prime numbers:
p and q
p and q should have high bit-length
p and q should be chosen at random

20. RSA - Generating the two keys
(2) Compute
n = pq
n is the "modulus" for both the public
and private keys

21. RSA - Generating the two keys
(3) Compute
φ(n) = φ(p)φ(q) = (p − 1)(q − 1)

22. RSA - Generating the two keys
(4) Choose e such that
1 < e < φ(n)
and
gcd(e, φ(n))
TIP: e and φ(n) are coprime

23. RSA - Generating the two keys
"e" is the Public Key Exponent

24. RSA - Generating the two keys
(5) Compute d where
d−1
≡ e (mod φ(n))
or
d is the multiplicative inverse of
e (modulo φ(n))

25. RSA - Generating the two keys
To calculate d
solve for d given
d*e ≡ 1 (mod φ(n))

26. RSA - Generating the two keys
Public Key: e and n
Private Key: d and n
d, p, q and φ(n) must be kept secret