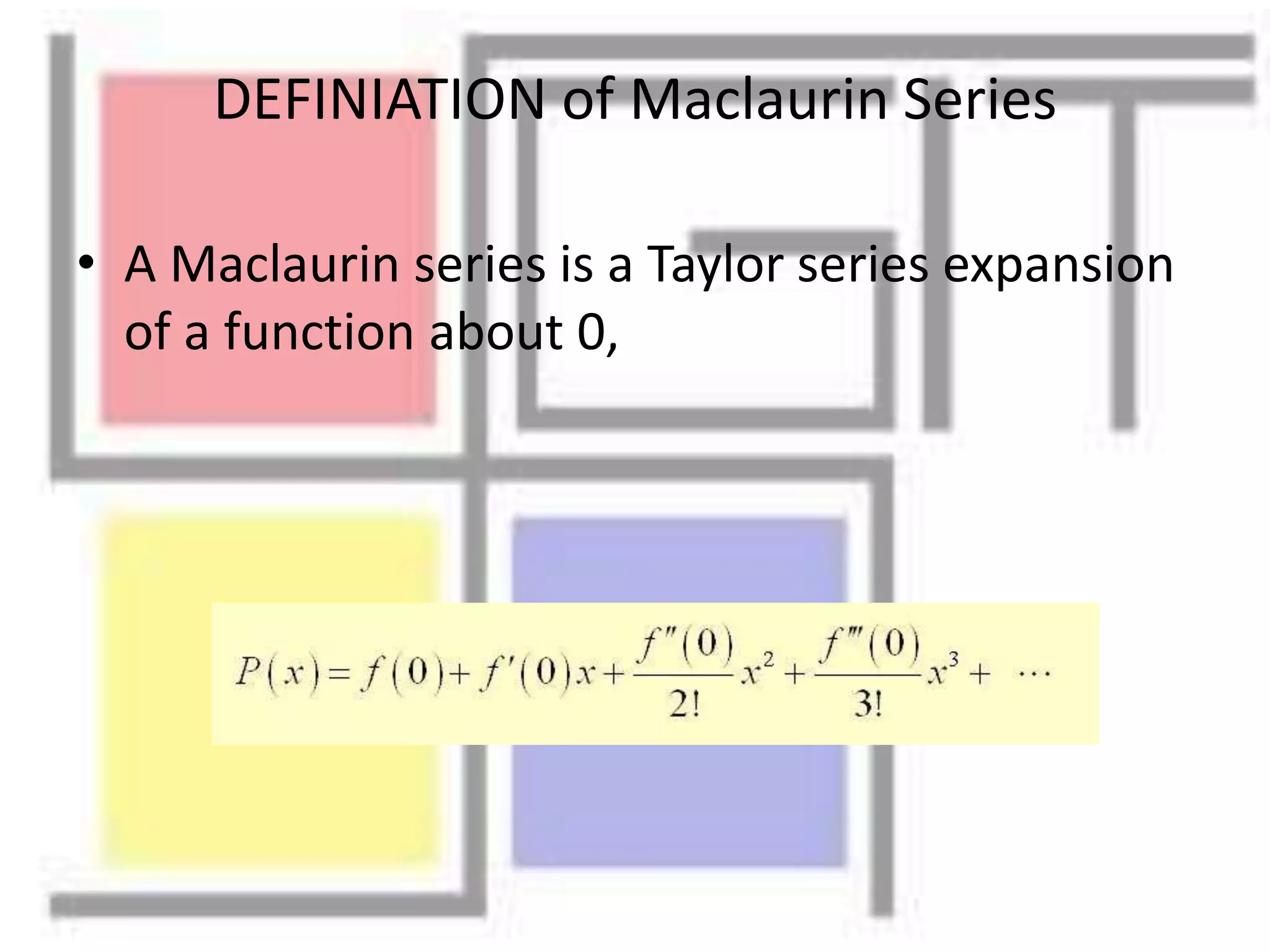
Taylor and Maclaurin Series are representations of functions as infinite sums of terms calculated from the function's derivatives at a single point. Specifically, a Taylor series expands a function around some point a, while a Maclaurin series is the special case of a Taylor series expanded around zero. Examples are provided of using Taylor series to expand the square root function around 1 and finding the Maclaurin series for the sine function.

1. Taylor and Maclaurin Series
Prepared By : Sandip Panchal
Made By : Harsh Pathak
Subject : Calculus

2. CONTENT
• INTODUCTION
• DEFINIATION of Taylor Series
• DEFINIATION of Maclaurin Series
• Examples

3. INTODUCTION
• Taylor series is a representation of a function as an infinite sumvof terms
that are calculated from the values of the function's derivatives at a single
point.
• The concept of a Taylor series was formulated by the Scottish
mathematician James Gregory and formally introduced by the English
mathematician Brook Taylor in 1715. If the Taylor series is centered at
zero, then that series is also called a Maclaurin series, named after the
Scottish mathematician Colin Maclaurin , who made extensive use of this
special case of Taylor series in the 18th century.

4. DEFINIATION of Taylor Series
• The Taylor series of a real or complex-valued
function f ( x ) that is infinitely differentiable
at a real or complex number a is the power
series

5. DEFINIATION of Maclaurin Series
• A Maclaurin series is a Taylor series expansion
of a function about 0,

6. Examples
Example 1 : Expand √x in powers of (x-1)

7. Example 2: Find the Maclaurin series for sinx