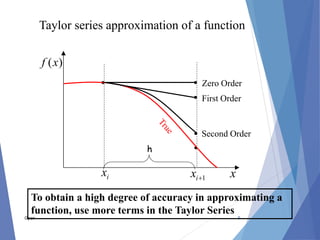
The document provides an overview of Taylor series, including its definition, application for approximating function values, and finite difference approximations for derivatives. It explains that any smooth function can be approximated by a polynomial, with the Taylor expansion formula featured prominently. Examples and exercises are included to illustrate finding Taylor series for specific functions like sin(x) and cos(x).

1. Taylor Series
1
Open

2. At the end of the lecture you
will be able to
 Understand Taylor series and how to use it to
approximate the values of a function
 Understand how to write forward, backward,
and centered finite difference approximation
for first and second derivative.
2
Open

3.  This theorem states that any smooth
function can be approximated by a
polynomial
 Using it, we can predict the value of
a function at one point in terms of
the values of the function and its
derivatives at another point
3
Open

4. Quick Notes on Taylor Series
 The Taylor expansion about x=a, is given as
 with
 Is called as the remainder or error of the Taylor series
4
Open

5. 5
To obtain a high degree of accuracy in approximating a
function, use more terms in the Taylor Series
i
x 1

i
x x
)
(x
f
Zero Order
First Order
Second Order
h
Taylor series approximation of a function
Open

6. If a=0, the Taylor series is known
as Maclaurin series.
6
Open

7. or
7
Open

8. Example 3
Solution.
Thus
8
Open

9. Example 4
 Find the Taylor series of sin(x) about x=0.
 Solution:
9
Open

10. 10
This pattern will repeat. Thus the Taylor series for sin(x)
about x=0 is
Find the Taylor series for f(x)=cos(x) about x=0 and x=pi/4.
Open
Exercise

11. Exercise
Use zero- through third-order Taylor series expansions to
predict f(2) for
f(x) = 25x3 - 6x2 +7x - 88
using a base point at x =1. Compute the true percent relative
error t for each approximation.
11
Open